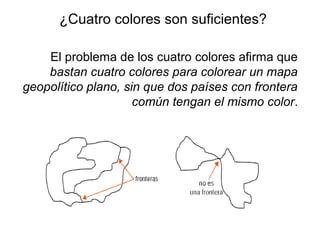
El documento trata sobre la idea de la demostración en la historia de las matemáticas. Se discuten conceptos como la definición rigurosa de conceptos matemáticos, la justificación de cada paso de una prueba y el uso de la intuición. También se mencionan temas como la independencia del cálculo de la geometría y la formalización de los procesos infinitos. Finalmente, se analiza brevemente la demostración del problema de los cuatro colores realizada con ayuda de computadora.

1. VI SIMPOSIO DE
MATEMÁTICAS Y
EDUCACIÓN
MATEMÁTICA
V CONGRESO
INTERNACIONAL DE
MATEMATICA ASISTIDA
POR COMPUTADOR

2. LA IDEA DE LA
DEMOSTRACION EN LA
HISTORIA DE LA
MATEMATICA
Juan E. Nápoles Valdes
UNNE-FaCENA
UTN-FRRE
ARGENTINA

5. -Cada concepto matemático debía ser explícitamente
definido en términos de otros conceptos cuya
naturaleza era suficientemente conocida.
-Las pruebas de los teoremas debían ser
completamente justificadas en cada una de sus
etapas, o bien por un teorema anteriormente probado,
por una definición, o por un axioma explícitamente
establecido.
-Las definiciones y axiomas escogidos debían ser lo
suficientemente amplios para que pudiesen cubrir los
resultados ya existentes.
-La intuición (geométrica o física) no era un criterio
válido para desarrollar una prueba matemática.
La argumentación reposa en un punto de partida
conformado por razones consensuales para un grupo
de “entendidos”.

7. Incorrecta comprensión del concepto de
diferencial
Insuficiente comprensión del concepto de
función
Ausencia de un concepto claro de límite
El concepto de continuidad funcional era intuitivo
Concepto difuso de integral definida
Se necesitaba tener una clara comprensión de
lo que era un sistema numérico

12. Sea f(x) con período 2L, f(x+2L)=f(x)
0
1
( ) cos sin
2
n n
n
a nx nx
f x a b
L L
π π∞
=
= + +∑
1
( )cos
c L
n
c
nx
a f x dx
L L
π+
= ∫
1
( )sin
c L
n
c
nx
b f x dx
L L
π+
= ∫

13. 1 0
( )
1 2
for x
f x
for x
π
π π
< <
= 
− < <
4 sin sin3 sin5
( )
1 3 5
x x x
f x
π
 
= + + + ÷
 
L

16. Riemann Hypothesis – Most famous unsolved problem in mathematics
The non-trivial zeros of the zeta function lie on the line x = ½ in the
complex plane

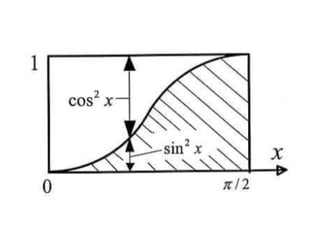
18. 1. Se ha hecho realidad la independencia de las nociones fundamentales del
Cálculo de la Geometría. En particular, el concepto de integral no solamente se
expresa en términos analíticos, sino que se piensa en un nivel de gran
generalidad, que no parece tener relación con la intuición geométrica del área.
Más aún, estamos “ad portas” de una teoría tan general de la integral, en la cual
la noción de área es obtenido desde esta teoría, más allá de la intuición
euclidiana.
2. Las pruebas de existencia adquieren legitimidad y validez de una manera radical;
además de la prueba de la existencia de una función continua sin derivada (de
hecho se está demostrando el teorema moderno: “Existen funciones continuas
sobre [0,1], que no son derivables en ningún punto de [0,1]”) que hemos
valorado, están los teoremas de existencia de Peano de fines de siglo.
3. El afianzamiento del método deductivo en las demostraciones de los teoremas,
primero limitadamente con trabajos como las “Lecciones de Geometría
Moderna” de Moritz Pasch, profesadas en 1873 y publicadas en 1882; pero que
termina avasalladoramente con los famosos “Grundlagen der Geometrie” de
Hilbert de 1899, que confieren sello riguroso al tradicional método euclídeo y lo
convierten en un proceso de alcance mayor y fecundo en problemas de toda
índole.
4. Y, finalmente, el punto más importante es el de la formalización y estatus que
adquieren los procesos infinitos, abonando el terreno para la implantación del
infinito actual como objeto real matemático.

20. ¿Cuatro colores son suficientes?
El problema de los cuatro colores afirma que
bastan cuatro colores para colorear un mapa
geopolítico plano, sin que dos países con frontera
común tengan el mismo color.

23. Se trata claramente un problema topológico, pues no
importa la forma de las regiones, sino como están
colocadas las unas respecto a las otras.

24. • 1852 Francis Guthrie plantea el problema
a su hermano Frederick y a Augustus de
Morgan. Éste último se lo comunica a Sir
Rowan Hamilton.
• 1878 Arthur Cayley publica el enunciado
de la conjetura.
• 1879 Sir Alfred Bray Kempe publica su
demostración.

25. En 1890, Heawood prueba el problema de los cinco colores,
usando precisamente el argumento de las cadenas de Kempe.
El concepto de reducibilidad fue introducido formalmente en
1913 por George David Birkhoff en su trabajo “The
reducibility of maps”. Esencialmente se refiere a cuando una
configuración puede reducirse a un caso más simple, que por
inducción se puede asumir coloreable con cuatro colores.
En 1969, Heinrich Heesch sistematiza la prueba de la
reducibilidad, desarrollando un algoritmo que intenta
implementar con ordenador. Realiza diversos tests con el
programa Algol 60 en un CDC1604A. Afirma que la conjetura
puede resolverse considerando 8900 configuraciones.
Además, inventa la construcción de conjuntos inevitables
(obstrucciones locales) a través de su llamado algoritmo de
descarga.

26. La primera prueba de Appel, Haken y Koch usó un
algoritmo de descarga muy complicado, que produjo una
lista de 1936 configuraciones inevitables, cada una de las
cuales se demostró reducible, con la ayuda de un
ordenador. Se probó que 102 de estas configuraciones
eran redundantes, así que el número requerido para la
prueba era de solamente 1834.
Modificando consecutivamente el algoritmo de descarga
(para producir un conjunto inevitable cada vez mejor),
encontraron un algoritmo de descarga (con 300 reglas)
que produjo un conjunto de 1468 configuraciones
inevitables; se demostró que eran reducibles con la ayuda
de un ordenador programado por Koch para buscar las
extensiones requeridas del coloreado, que llevó 1200
horas de cálculo en un IBM 360. La demostración fue
completada por Appel y Haken en 1976.

27. [1] K. Appel and W. Haken, Every planar map is four
colourable, Part I: discharging, Illinois Journal of Maths 21,
429-490, 1977.
[2] K. Appel, W. Haken and J. Koch, Every planar map is
four colourable, Part II: reducibility, Illinois Journal of
Maths 21, 491-567, 1977.

29. 1) Ha servido de estímulo en el desarrollo de teorías
matemáticas como la teoría de grafos y de redes;
2) es el primer gran teorema probado usando un
ordenador; aunque la corrección de la compilación no ha
sido probada y la infalibilidad del hardware no ha sido
demostrada.
Este último asunto levantó muchas controversias en el
momento de la publicación de su demostración, aplacadas
gracias a la aparición de otras pruebas realizadas con
ayuda de ordenador, como la clasificación de los grupos
simples finitos (que depende de cálculos imposibles de
ejecutar con detalle a mano), o la solución de Hales del
problema de Kepler sobre el empaquetamiento óptimo de
esferas.

30. Paul Halmos opina que la demostración realizada con un
ordenador tiene la misma credibilidad que si está hecha por un
adivino, las máquinas tienen algunas propiedades físicas que
aún tenemos que entender. “No puedo aprender nada de la
demostración. La prueba no indica la razón por la que sólo se
necesitan cuatro colores ¿por qué no trece? ¿Qué tiene de
especial el número cuatro?”
Pierre Deligne (Medalla Field en1978) opina “No creo en una
prueba hecha con ordenador. En primer lugar, soy demasiado
egocéntrico. Creo en una demostración si la entiendo, si está
clara. Un ordenador puede también cometer errores, pero es
mucho más difícil encontrarlos”.

31. Los no escépticos argumentan que la queja de que los
ordenadores tienen virus o producen errores, se puede
aplicar de la misma manera a las personas, que se
equivocan muy a menudo. Aunque los errores cometidos
por los ordenadores son más difíciles de detectar, los
humanos fallan con más frecuencia. Los ordenadores
siguen un programa rígido predeterminado, y no tienen
distracciones motivadas por los cambios de humor, el
estrés u otros factores externos.
“Como el problema se ha obtenido por medios
totalmente inapropiados, ningún matemático de primera
fila debería trabajar más en ello y por lo tanto una
demostración decente puede ser retrasada
indefinidamente... Así que hemos hecho una cosa mala,
muy mala y pienso que una cosa similar no debería
cometerse nunca más”.

32. “Las matemáticas forman parte de la física. La física
es una ciencia experimental, una de las ciencias
naturales. Las matemáticas son la parte de la física
en la que los experimentos son baratos”

35. “Discovering theorems with a computer: the
case of y’=sin(xy)”, American Mathematical
Monthly, November 86(1979), 733-739 de Wendell
Mills, Boris Weisfeiler and Alan M. Krall.

37. Lema 1. Sea y(x) una solución de y’=sen(xy).
Entonces:
a) Si y(x) intersecta a xy=nπ, lo hace con pendiente
cero.
b) Si y(x) intersecta a xy=(n+1/2)π, lo hace con
pendiente (-1)n
.

38. La suma de los ángulos de un triángulo es 180 grados.

39. Cuadrado de una suma

40. Cuadrado de una diferencia

41. J.A. Garfield (1876)

42. Suma de impares
1 = 13
3 + 5 = 23
7 + 9 + 11 = 33
13 + 15 + 17 + 19 = 43

48. •estética
•ética pedagógica
•pensamiento geométrico espacial
•formación lingüística
•rigor en sus razonamientos, la exigencia
y el carácter reflexivo

49. argumentar, fundamentar, inferir, probar,
deducir, refutar y demostrar
abstraer, concretar, analizar, sintetizar,
comparar, clasificar, particularizar y
generalizar
métodos y procedimientos

50. tenacidad, perseverancia, esfuerzo,
disciplina y constancia
reto intelectual

51. •Es conveniente enseñar a “demostrar” en un
sistema educativo generalizado.
•Es necesario enseñar a “demostrar” en un
sistema educativo generalizado. Contribuye,
entre otros, al desarrollo del pensamiento, de
operaciones mentales generales, de
habilidades generales y específicas, así como
a la formación lingüística.
•Es necesario dosificar la inserción de las
argumentaciones, pruebas y demostraciones
en el curriculum escolar.