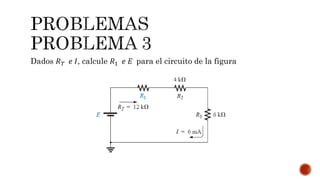
El documento describe los conceptos básicos de circuitos eléctricos, incluyendo los tipos de corriente, componentes de circuitos, y cómo calcular la resistencia total, corriente y potencia en circuitos en serie. Explica que la resistencia total de circuitos en serie es la suma de las resistencias individuales, y que la corriente es la misma a lo largo de todos los elementos en serie.

1. Clase 3a
27-01-2014

2.  Existen dos tipos de corriente disponibles para el consumidor de hoy.
Uno es la corriente directa (cd), en la que idealmente el flujo de
carga (corriente) no cambia en magnitud (o dirección) con el tiempo.
 La otra es la corriente alterna senoidal (ca), en la que el flujo de
carga se encuentra cambiando continuamente en magnitud (y
dirección) con el tiempo.

3.  La bacteria entre sus terminales, tiene la habilidad de causar que la
carga fluya a través del circuito simple. Como se muestra en la
siguiente figura.

4. Presentación de los componentes básicos de un circuito

5.  Si consideramos el cable un conductor ideal (es decir, que no
presenta resistencia al flujo), la diferencia de potencial 𝑉 en el
resistor será igual al voltaje aplicado de la batería: 𝑉 𝑣𝑜𝑙𝑡𝑠 =
𝐸 (𝑣𝑜𝑙𝑡𝑠).
 La resistencia esta únicamente limitada por el resistor 𝑅. Mientras
mayor sea la resistencia, menor será la corriente y de forma
reciproca, según lo determina la ley de ohm.
 Al seguir la dirección del flujo convencional, se observa que existe
una elevación de potencial a través de la batería (− 𝑎 +), y una caída
de potencial a través del resistor (+𝑎 −).

6.  Para circuitos de cd con una sola fuente de voltaje, el flujo convencional
pasa siempre de un potencial bajo a un potencial alto cuando atraviesa
una fuente de voltaje, como se muestra la siguiente figura.
 Definición de la dirección del flujo convencional para circuitos de cd con una sola
fuente

7.  Sin embargo el flujo convencional siempre atraviesa de un potencial
alto a uno bajo cuando pasa a través del resistor para cualquier
numero de Fuentes de voltaje dentro del mismo circuito, como se
muestra en la figura.
 Para todos los circuitos de cd con una fuente de voltaje

8.  Un circuito consta de cualquier número de elementos conectados en
puntos terminales, ofreciendo al menos una ruta cerrada por la cual
pueda fluir la carga.
 El circuito de la figura cuenta con tres elementos conectados en tres
puntos terminales (𝑎, 𝑏 𝑦 𝑐) para obtener una ruta cerrada para la
corriente.

10.  Dos elementos se encuentran en serie si:
1. Solo cuentan con una terminal en común (es decir, una terminal de
un elemento se encuentra conectada solamente a una terminal de
otro elemento).
2. El punto común entre los dos elementos no se encuentra conectado
con otro elemento que transporta corriente.

11. Si el circuito anterior se modificara de forma que se insertara un
resistor 𝑅3 que transporte corriente como se muestra en la figura, los
resistores 𝑅1 𝑦 𝑅2 ya no estarán en serie debido a la violación del
inciso 2 de la definición anterior.
𝑅1 𝑦 𝑅2 ya no están en serie

12.  La corriente es la misma a lo largo de los elementos en serie.
 Una rama de un circuito es cualquier segmento del circuito que
cuente con uno o más elementos en serie. (el resistor 𝑅1 forma una
rama del circuito, el resistor 𝑅2 otra y la batería 𝐸 una tercera.
 La resistencia total de un circuito en serie es la suma de los niveles
de resistencia.

13.  En general, para calcular la resistencia total de 𝑁 resistores en
serie, se aplica la siguiente ecuación:
 𝑅 𝑇 = 𝑅1 + 𝑅2 + 𝑅3 + ⋯ + 𝑅 𝑁 𝑜ℎ𝑚𝑠, Ω
𝑅𝑒𝑠𝑖𝑠𝑡𝑒𝑛𝑐𝑖𝑎 𝑂𝑏𝑠𝑒𝑟𝑣𝑎𝑑𝑎 𝑝𝑜𝑟 𝑙𝑎 𝑓𝑢𝑒𝑛𝑡𝑒

14.  Una vez que se conoce la Resistencia total del circuito puede
volverse a trazar como se muestra, mostrando claramente que la
única Resistencia que la fuente “observa” será la Resistencia total.
 La corriente extraída de la fuente puede determinarse utilizando la
ley de Ohm de la siguiente forma:
𝐼𝑠 =
𝐸
𝑅 𝑇
𝑎𝑚𝑝𝑒𝑟𝑒, 𝐴

15. 𝑅𝑒𝑒𝑚𝑝𝑙𝑎𝑧𝑜 𝑑𝑒 𝑙𝑜𝑠 𝑟𝑒𝑠𝑖𝑠𝑡𝑜𝑟𝑒𝑠 𝑒𝑛 𝑠𝑒𝑖𝑟𝑒 𝑅1 𝑦 𝑅2

16.  Dado que 𝐸 es fija, la magnitud de la corriente de la fuente será
totalmente dependiente de la magnitud de 𝑅 𝑇.
 Una 𝑅 𝑇 mas grande dará por resultado un valor relativamente
pequeño de 𝐼𝑠 mientras que un menor valor 𝑅 𝑇 ocasionará niveles
más altos de corriente.
 El hecho de que la corriente sea la misma por cada elemento permite
un calculo directo del voltaje en cada resistor utilizando la ley de Oh;
es decir,
𝑉1 = 𝐼𝑅1, 𝑉2 = 𝐼𝑅2, 𝑉3 = 𝐼𝑅3, … , 𝑉𝑁 = 𝐼𝑅 𝑁 𝑣𝑜𝑙𝑡𝑠

17.  La potencia entregada a cada resistor puede entonces determinarse
utilizando cualquiera de las tres ecuaciones que a continuación se
presentan para 𝑅1:
𝑃1 = 𝑉1 𝐼1 = 𝐼1
2
𝑅1 =
𝑉1
2
𝑅1
(𝑤𝑎𝑡𝑡𝑠, 𝑤)

18.  La potencia entregada por la fuente
 La potencia total entregada a un circuito resistivo será igual a la
potencia total disipada por los elementos resistivos.
𝑃𝑑𝑒𝑙 = 𝐸𝐼 (𝑤𝑎𝑡𝑡𝑠, 𝑊)
𝑃𝑑𝑒𝑙 = 𝑃1 + 𝑃2 + 𝑃3 + ⋯ + 𝑃 𝑁 (𝑤𝑎𝑡𝑡𝑠, 𝑊)

19. a. Calcule la resistencia total del circuito en serie de la figura
b. Calcule la corriente de la fuente 𝐼𝑆
c. Determine los voltajes 𝑉1, 𝑉2 𝑦 𝑉3
d. Calcule la potencia disipada por 𝑅1, 𝑅2 𝑦 𝑅3
e. Determine la potencia entregada por la fuente, y compárela con la
suma de los niveles de potencia del inciso (d)

21. a. Calcule la resistencia total del circuito en serie de la figura
b. Calcule la corriente de la fuente 𝐼𝑆
𝑅 𝑇 = 𝑅1 + 𝑅2 + 𝑅3 = 2Ω + 1Ω + 5Ω = 8Ω
𝐼𝑆 =
𝐸
𝑅 𝑇
=
20𝑉
8Ω
= 2.5𝐴

22. c. Determine los voltajes 𝑉1, 𝑉2 𝑦 𝑉3
d. Calcule la potencia disipada por 𝑅1, 𝑅2 𝑦 𝑅3
𝑉1 = 𝐼𝑅1 = 2.5𝐴 2Ω = 5𝑉
𝑉2 = 𝐼𝑅2 = 2.5𝐴 1Ω = 2.5𝑉
𝑉3 = 𝐼𝑅3 = (2.5𝐴)(5Ω) = 12.5𝑉
𝑃1 = 𝑉1 𝐼1 = 5𝑉 2.5𝐴 = 12.5𝑊
𝑃2 = 𝐼2
2
𝑅2 = (2.5𝐴)2 1Ω = 6.25𝑊
𝑃3 =
𝑉3
2
=
2.5𝐴 2
= 31.25𝑊

23. e. Determine la potencia entregada por la fuente, y compárela con la
suma de los niveles de potencia del inciso (d)
𝑃𝑑𝑒𝑙 = 𝐸𝐼 = 20𝑉 2.5𝐴 = 50𝑊
𝑃𝑑𝑒𝑙 = 𝑃1 + 𝑃2 + 𝑃3
50𝑊 = 12.5𝑊 + 6.25𝑊 + 31.25𝑊
50𝑊 = 50𝑊 (𝑠𝑒 𝑐𝑜𝑚𝑝𝑟𝑢𝑒𝑏𝑎)

24. Para calcular la resistencia total de 𝑁 resistores del mismo valor en
serie, simplemente multiplique el valor de uno de los resistores por el
numero en serie; es decir,
𝑅 𝑇 = 𝑁𝑅

25. Determine 𝑅 𝑇, 𝐼 𝑦 𝑉2 para l circuito de la siguiente figura.

26. Solución
Observe la dirección de la corriente según la establece la batería y la
polaridad de la caída de voltaje en 𝑅2 como la determina la dirección
de la corriente. Dado que 𝑅1 = 𝑅3 = 𝑅4.
𝑅 𝑇 = 𝑁𝑅1 + 𝑅2 = 3 7Ω + 4Ω = 21Ω + 4Ω = 25Ω
𝐼 =
𝐸
𝑅 𝑇
=
50𝑉
25Ω
= 2𝐴
𝑉2 = 𝐼𝑅2 = 2𝐴 4Ω = 8𝑉

27. Dados 𝑅 𝑇 𝑒 𝐼, calcule 𝑅1 𝑒 𝐸 para el circuito de la figura

28. Solución
𝑅 𝑇 = 𝑅1 + 𝑅2 + 𝑅3
12𝑘Ω = 𝑅1 + 4𝑘Ω + 6𝑘Ω
𝑅1 = 12𝑘Ω − 10𝑘Ω = 2𝑘Ω
𝐸 = 𝐼𝑅 𝑇 = 6 × 10−3
𝐴 12 × 103
Ω = 72𝑉