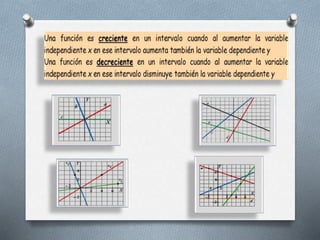
Este documento presenta una lección sobre funciones lineales. Explica que una función lineal tiene la forma f(x)=mx+n, donde m es la pendiente y n es la ordenada al origen. Las funciones lineales se grafican como rectas, y su gráfica siempre pasa por el origen. El documento también cubre cómo calcular la pendiente y ecuación de una recta dados dos puntos sobre ella. Finalmente, proporciona ejercicios para que los estudiantes practiquen conceptos como calcular pendientes e identificar las características de funciones dadas.

1. UNIDAD EDUCATIVA
DEL MILENIO CACIQUE
TUMBALÁ
CLASE DEMOSTRATIVA
TEMA: FUNCIONES LINEALES
AUTOR LIC. JOSÉ GERARDO
CHACÓN TORRES
ZUMBAHUA 2014-2015

2. Cantidad de litros Precio ($)
0,5
1 15
2 ...
10 ...
50 ...
100 ...
200 ...
... 7500
... 15000
... 30000
Cantidad de litros Precio ($)
0,5
1 24,50
2 ...
10 ...
50 ...
100 ...
200 ...
... 12250
... 24500
... 49000
EVALUACIÓN DE ENTRADA
En una estación de servicio se vende combustible a estos precios: Gasoil $15,00 el litro, Nafta Común $24,50 el
litro.
Completar las siguientes tablas
Gasoil Nafta Común

3. FUNCIONES LINEALES
Toda función lineal tiene forma :
f(x) = m x + n, Se denota con Y =
f(x)=g(x)=h(x)
Aquí
x : variable independiente.
Y : variable dependiente.
m : coeficiente de dirección o pendiente de
la recta.
n : coeficiente de posición u ordenada en el
origen.

4. La gráfica de una función
lineal
La gráfica de una función lineal es el conjunto
de puntos (x, y) del plano tales que y = m ∙ x
Observa que: Esta gráfica es una recta que
pasa por el origen
La constante de proporcionalidad, m, se llama
pendiente de la recta y caracteriza la función
Si m > 0 la función y = m ∙ x es creciente.
Si m < 0 la función y = m ∙ x es decreciente.
Si m = 0 la función y = 0 es constante. Su
gráfica es el eje de abscisas.

7. Ecuaciones de la forma punto-pendiente
La ecuación de la recta que pasa por un punto (x1,
y1) con pendiente m en la forma punto-pendiente es
y – y1 = m(x – x1).
Ejercicios para discusión: Halla la ecuación de la
recta dados los elementos:
m = -3, punto (8, 0)

8. Las funciones lineales se representan gráficamente como
____________________________.
La gráfica de todas las funciones lineales pasa por el punto
__________________________.
Para dibujar la gráfica basta con obtener otro punto y unirlo con
______________________.
Si m es positiva, representa
___________________________________________________.
y = -2x y = -0.5x y = 0.2x y = 2x
Pendiente
ACTIVIDAD DENTRO DEL AULA
Completa:
Averigua la pendiente de cada una de las funciones anteriores.

9. y = -2x + 2 y = 2x - 2 y = 0.5x - 1 y = -0.5x + 3
m
n
Averigua la pendiente y la ordenada en el origen de cada una de las funciones anteriores.
P(2,-3), Q(2,1) P(2,-3), Q(-1,-3) P(0,2), Q(0,-2) P(2,0), Q(-2,0)
Representa gráficamente las rectas que pasan por los puntos que se indican y halla las ecuaciones de
dichas rectas:

10. APLICACIÓN A LA VIDA
DIARIA

11. EVALUACIÓN FINAL
f1 (x)= x+2 f2(x)= 2x+1 f3(x)= ½x-1
f4 (x)= 3x-5 f(x)5 = 3 f6(x)= x
función f1=x+2 f2 = 2x+1 f3 = ½x-1 f4 = 3x-5 f5 = 3 f6 = x
pte: m
OaO: b
Dadas las siguientes funciones:
a) En la siguiente tabla colocar los valores de la pendiente (pte) m y la
ordenada al origen (OaO) b.

12. TAREA PARA LA SIGUIENTE
CLASE
Halla la pendiente de la recta que pasa por
cada par de puntos.
1) (-3 , -3) y (2, -3)
2) (0, 4) y (2, -4)
3) (-2, -1) y (1, 2)
4) (-3, 2) y (-3, -1)

13. BIBLIOGRAFÍA
Libro 2002 nm3
Ies Barallabre matemática 3ro ESO
“Cesario Rodriguez.
Funciones y gráficas.1 ptt (web)
Pendiente de una recta.doc (web)