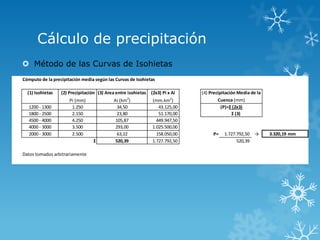
El documento describe cuatro métodos para calcular la precipitación media en una cuenca: el método aritmético, el método de los polígonos de Thiessen, y el método de las curvas isoyetas. Explica cada método y proporciona ejemplos numéricos de cómo aplicarlos para estimar la precipitación media en una cuenca hidrográfica.

1. República Bolivariana de Venezuela
Instituto Universitario Politécnico
“Santiago Mariño”
Facultad: Ingeniería
Carrera: Ingeniería Civil
Extensión Guayana
Cátedra: Hidrología
T.S.U. Subero Lanni
Puerto Ordaz, Mayo de 2013
Prof. Enid Moreno

2. Métodos de Cálculo de precipitación
 Método Aritmético
Donde:
P: Precipitación Media estimada en el área
Pi: Precipitación Observada en la Estación i
n: Número de estaciones dentro de los
límites de la cuenca de estudio
 Método de los Polígonos de Thiessen
Donde:
P: Precipitación Media estimada en el área
Pi: Precipitación Observada en la Estación i
n: Número de estaciones dentro de los límites de la
cuenca de estudio
Ai: área del polígono correspondiente a la estación i
A: área total de la cuenca

3.  Método de los Polígonos de Thiessen
1.- Se conectan las estaciones
contiguas mediante líneas rectas en
tal forma que no hayan
interceptación. Conformando
triángulos
2.- Se trazan mediatrices
perpendiculares prolongándose
hasta que se corten con otras
mediatrices vecinas
3.- Los puntos de cruce entre las
mediatrices representan el área de
influencia de la estación
Métodos de Cálculo de precipitación

4.  Método de las curvas isoyetas
Donde:
P: Precipitación Media estimada en el área
Pj: valor de la precipitación de la Isoyeta j
Aj: área incluida entre dos isoyetas
consecutivas (j y j+1)
m: número total de isoyetas
Sobre la base de los valores puntuales de precipitación
en cada estación (como los enmarcados en un cuadro
rojo) dentro de la cuenca, se construyen, por
interpolación, líneas de igual precipitación
Métodos de Cálculo de precipitación

5. Cálculo de precipitación
 Método Aritmético
Cómputo de la precipitación media Método de la Media Aritmética, P
Estación Precipitación
Pi (mm)
Pi x Ai (mm.km2
)
1 1.489 1.489
2 1.523 3.046 Σ
3 920,7 2.762 n
4 1.125 4.500
5 1.862 9.310 21.107 → 4.221,40 mm
Σ 21.107 5
P =
P =

6. Cálculo de precipitación
Cómputo de la precipitación media según polígonos de Thiessen
(1) Estación Ei (2) Precipitación
Pi (cm/año)
(3) Area de la Estación i
Ai (km2
)
(2 x3) Pi x Ai
(cm.km2
)
Aripichi 256 24.025 6.150.400
Capaura 282 30.900 8.713.800
Arekuna 303 41.750 12.650.250
Karún 354 22.225 7.867.650 P= 45.663.225,00 → 308,48 cm
Auraima 353 29.125 10.281.125 148.025,00
Σ 148.025 45.663.225
datos para el cálculo tomados de:
http://www.saber.ula.ve/bitstream/123456789/31157/1/ponencia_2006.pdf
Precipitación en cm período 1986 - 2001
(4) Precipitación Media de la
Cuenca (cm)
(P)=Σ (2x3)
Σ (3)
Río Paragua en:
Río Caroní en:
 Método de los Polígonos de Thiessen

7. Cálculo de precipitación
 Método de las Curvas de Isohietas

8. Cálculo de precipitación
 Método de las Curvas de Isohietas
Cómputo de la precipitación media según las Curvas de Isohietas
(1) Isohietas (2) Precipitación
Pi (mm)
(3) Area entre isohietas
Ai (km2
)
(2x3) Pi x Ai
(mm.km2
)
1200 - 1300 1.250 34,50 43.125,00
1800 - 2500 2.150 23,80 51.170,00
4500 - 4000 4.250 105,87 449.947,50
4000 - 3000 3.500 293,00 1.025.500,00
2000 - 3000 2.500 63,22 158.050,00 P= 1.727.792,50 → 3.320,19 mm
Σ 520,39 1.727.792,50 520,39
Datos tomados arbitrariamente
(4) Precipitación Media de la
Cuenca (mm)
(P)=Σ (2x3)
Σ (3)