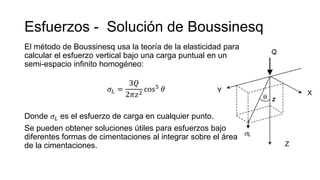
Settle3 es un programa para calcular asentamientos causados por cimentaciones, terraplenes y cargas. Puede analizar asentamientos instantáneos y diferidos utilizando datos de CPT, SPT y velocidad de onda cortante. Calcula esfuerzos y asentamientos usando métodos como Boussinesq, multicapa y Westergaard, y modela asentamientos primarios y secundarios para suelos lineales y no lineales.

1. ¿Cómo funciona Settle3?
Ing. Rafael Ortiz Hernández
Geotecnia
División de Investigación y Posgrado Facultad de Ingeniería
Universidad Autónoma de Querétaro

2. Antecedentes
• Settle3 es un programa desarrollado por Rocscience, una
empresa de software geotécnico.
• Originalmente se publico la versión 1.0 en 2008.
• Al momento se tiene la versión 5.015 publicada en 25 de
abril de 2022.

3. ¿Qué podemos hacer con Settle3?
• Se pueden realizar cálculos de deformaciones como asentamientos
instantáneos y diferidos en el tiempo.
• Estas deformaciones son provocadas por cimentaciones,
terraplenes, cargas.
• Análisis de asentamientos y licuación con información de CPT.
• Adicional al CPT, se puede analizar el asentamiento con datos de
SPT y velocidad de onda de corte.
• Los modelos de suelo pueden ser perfectamente horizontales o
contemplar estratigrafía no horizontal.
• Calculo de asentamientos considerando mejoramiento de suelos.

4. Esfuerzos
1. Esfuerzos efectivos
El asentamiento depende del esfuerzo efectivo. El esfuerzo efectivo es
el esfuerzo total debido a la gravedad y cargas externas menos la
presión de poro. El esfuerzo efectivo vertical en cualquier punto es:
𝜎′
= 𝜎 − 𝑢
Donde:
𝜎 Esfuerzo vertical efectivo
𝑢 Presión de poro

5. Esfuerzos
1. Esfuerzo inicial y presión de poro
El esfuerzo inicial total es el esfuerzo por la carga de gravedad. En
cualquier punto este esfuerzo se encuentra al sumar los pesos de los
materiales encima de este punto. Por lo cual el esfuerzo total inicial en
cualquier punto es:
𝜎𝑖 = 𝛾𝐻
Donde:
𝛾 Peso unitario saturado o húmedo, dependiendo de su
ubicación relativa al nivel freático.
𝐻 Espesor de la capa

6. Esfuerzos
1. Esfuerzo inicial y presión de poro
La presión de poro inicial 𝑢𝑖 en cualquier punto es la presión debido al
peso del agua encima del punto. Si la altura del punto de interés es z y
el nivel de agua esta a la altura 𝑧𝑤𝑡, la presión inicial es:
𝑢𝑖 = 𝑧 − 𝑧𝑤𝑡 𝛾𝑤𝑎𝑡𝑒𝑟 si 𝑧 > 𝑧𝑤𝑡
𝑢𝑖 = 0 si 𝑧 ≤ 𝑧𝑤𝑡
Donde:
𝛾water Peso unitario del agua.

7. Esfuerzos
El esfuerzo inicial efectivo entonces se calcula con las
ecuaciones anteriores de la siguiente forma:
𝜎𝑖
′
= 𝜎𝑖 − 𝑢𝑖

8. Cambios de esfuerzos debido a cargas externas
• Las cargas externas pueden ser terraplenes, rellenos o
cimentaciones.
• Estas cargas externas pueden provocar un cambio es
esfuerzos totales dependiendo de la geometría y magnitud de
la carga externa.
• Settle3 usa 4 métodos:
1. Solución de Boussinesq
2. Solución 2:1
3. Solución multicapa
4. Solución Westergaard

9. Esfuerzos - Solución de Boussinesq
El método de Boussinesq usa la teoría de la elasticidad para
calcular el esfuerzo vertical bajo una carga puntual en un
semi-espacio infinito homogéneo:
𝜎𝐿 =
3𝑄
2𝜋𝑧2
cos5 𝜃
Donde 𝜎𝐿 es el esfuerzo de carga en cualquier punto.
Se pueden obtener soluciones útiles para esfuerzos bajo
diferentes formas de cimentaciones al integrar sobre el área
de la cimentaciones.

10. Esfuerzos - Solución 2:1
La solución asume que la zona de influencia
para una carga rectangular tiene una pendiente
2:1 y se calcula así:
𝜎𝐿 =
𝑄
𝐵 + 𝑧 𝐿 + 𝑧

11. Esfuerzos - Solución multicapa
La solución elástica completa para una cimentación de forma
arbitraria que descansa en un medio elástico en capas se calcula
por medio de la integración de la solución de carga puntual
(Método de Green) por medio de transformaciones de Hankel.
Se utilizan ecuaciones diferenciales parciales y condiciones de
frontera para cada capa y los esfuerzos relacionados.

12. Esfuerzos - Solución multicapa
Se necesitan dos niveles de integración numérica:
1. Evaluación de las soluciones de carga puntual.
2. La cuadratura numérica para evaluar los esfuerzos y
desplazamientos debido a la carga distribuida sobre un área.
Para ello las integrales de área en integrales de frontera.

13. Esfuerzos - Solución Westergaard
Estas ecuaciones asumen que el suelo es un medio elástico
pero con capas horizontales sin deformaciones laterales, donde
se tiene una gran distribución de esfuerzos laterales y tambien
se incluye la relación de Poisson del suelo.
Estas soluciones tiene una diferencia entre los resultados de la
solución de Boussinesq.

14. Esfuerzos - Solución Westergaard
• Carga puntual
𝜎𝑧 =
𝑄
𝑧2
1
2𝜋
1 − 2𝜈
2 − 2𝜈
1 − 2𝜈
2 − 2𝜈
+
𝑟
𝑧
2
3
2
• Carga circular
𝜎𝑧 = 𝑞 1 −
1
1 +
𝑎
𝑧
1 − 2𝜈
2 − 2𝜈
2

15. Esfuerzos - Solución Westergaard
• El esfuerzo de carga cimentación:
𝜎𝑧 =
𝑞
2𝜋
cot−1
1 − 2𝜈
2 − 2𝜈
1
𝑚2
+
1
𝑛2
+
1 − 2𝜈
2 − 2𝜈
2
1
𝑚2𝑛2
𝑚 =
𝐿
𝑧
; 𝑛 =
𝑊
𝑧

16. Cambio de esfuerzos por cambios en la altura del nivel de agua
• Si el nivel de agua se llega a reducir, algunos suelos cambiaran
de saturados a no saturados.
• Este cambio reducirá el esfuerzo total en todos los puntos
debajo de la altura inicial del nivel de agua.
• Este cambio también reducirá la presión de poro, por lo que se
incrementaran los esfuerzos efectivos.
• Esto pasa de forma inversa en el aumento del nivel de aguas,
los esfuerzos efectivos se reducirán.

17. Cambio de esfuerzos debido a la carga rígida
Se utiliza un método hibrido de minimización de errores basado
en cargas puntuales con la Función de Green.
El desplazamiento completo de una cimentación rígida sigue una
función linear con 3 variables desconocidas. La tracción de un
cuerpo elástico seguirá una función desconocida y en una
función más complicada.
Acoplar el cuerpo rígido y el cuerpo elástico se realiza al
minimizar el por medio de las diferencias cuadradas de las
diferencias entre desplazamientos.
Se publicó este método en Vijayakumar et al, 2009.

18. Esfuerzos horizontales
Se calculan los esfuerzos horizontales en las direcciones x y y
por medio de las siguientes ecuaciones:
𝜎𝑥0 = 𝑘0𝜎𝑧0
𝜎𝑦0 = 𝑘0𝜎𝑧0
𝜎𝑥𝑢 = 𝜎𝑦𝑢 = 𝜎𝑧𝑢
La disipación de exceso de presión de poro de una carga vertical
Δ𝑢𝑧, se aplica a los esfuerzos en todas las direcciones.

19. Asentamientos instantáneos
• Carga: El asentamiento ocurre al instante que se aplica la
carga y se asume elásticamente lineal.
• Esto se calcula con un módulo 1D y el esfuerzo efectivo.
• El módulo 1D se ingresa a Settle3 en las propiedades del
material.
• El módulo 3D se determina con el módulo 1D y la relación de
Poisson:
𝐸 = 𝐸𝑠
(1 + 𝜈)(1 − 2𝜈)
1 − 𝜈

20. Asentamientos instantáneos
La deformación vertical en cada subcapa se calcula por:
𝜀 =
Δ𝜎
𝐸𝑠
Δ𝜎 Es el cambio en esfuerzos totales verticales.
Con estos asentamientos iniciales se calculan con estas
deformaciones.

21. Asentamientos instantáneos
El asentamiento inicial, para cada línea, el punto de fondo se
asume que este fijo (no-móvil).
El desplazamiento vertical del segundo punto desde el fondo es
entonces:
𝛿 = Δ𝑧 = 𝜀ℎ
Donde:
ℎ espesor original de la subcapa de fondo.

22. Asentamientos instantáneos
El asentamiento del i-ésimo punto es
entonces el asentamiento del punto
debajo (i+1) más el asentamiento de
la capa i:
𝛿𝑖 = 𝛿𝑖+1 + 𝜀𝑖ℎ𝑖

23. Asentamiento inmediato con esfuerzo promedio
Por default, el asentamiento se calcula usando únicamente el
esfuerzo vertical.
Para un análisis más preciso, se utiliza el esfuerzo promedio 3D:
𝜎𝑀 =
1
3
𝜎𝑥𝑥 + 𝜎𝑦𝑦 + 𝜎𝑧𝑧 ; 𝜎𝑀 =
1
3
𝜎1 + 𝜎2 + 𝜎3

24. Asentamiento inmediato con esfuerzo promedio
El asentamiento inmediato se calcula con las deformaciones de cada
subcapa:
𝜀 =
1 + 𝜈 Δ𝜎 − 3𝜈 Δ𝜎𝑀
𝐸
𝜈 Relación de Poisson
Δ𝜎 Cambio en esfuerzo total vertical
Δ𝜎𝑀 Cambio es esfuerzo promedio
𝐸 Módulo de Young (no es el 1D, es el 3D)
El esfuerzo medio no se usa en el calculo de consolidación primaria y
secundaria porque la relación entre deformación y esfuerzo promedio no
esta definido claramente en materiales no lineales.

25. Asentamiento por consolidación primaria
Settle3 utiliza un calculo de asentamientos como definido
anteriormente:
𝛿𝑖 = 𝛿𝑖+1 + 𝜀𝑖ℎ𝑖
Pero las deformaciones varían de acuerdo al tipo de material:
1. Lineal
2. No lineal
3. Janbu
4. Koppejan

26. Modelo Lineal
Asume que los materiales son elásticamente lineales.
El cambio en deformación vertical para todo elemento con un
cambio es esfuerzos verticales efectivos Δ𝜎′ es:
Δ𝜀 = 𝑚𝑣Δ𝜎′
Donde 𝑚𝑣 es el módulo de compresibilidad unidimensional.
𝑚𝑣 =
Δ𝜀𝑣
Δ𝜎𝑣
′ =
−1
1 + 𝑒𝑜
𝑒1 − 𝑒𝑜
𝜎𝑣1
′
− 𝜎𝑣0
′

27. Modelo No lineal
En materiales no lineares el
módulo no es constante,
pero es una función del
esfuerzo.
Δ𝑒 = −𝐶𝑟 log
𝜎𝑓
′
𝜎𝑖
′
Δ𝑒 = −𝐶𝑐 log
𝜎𝑓
′
𝜎𝑖
′
𝜀 = −
Δ𝑒
1 + 𝑒𝑜

28. Modelo No Lineal
Δ𝜀 =
𝐶𝑟
1 + 𝑒𝑜
log
𝜎𝑓
′
𝜎𝑖
′
Δ𝜀 =
𝐶𝑐
1 + 𝑒𝑜
log
𝜎𝑓
′
𝜎𝑖
′
Δ𝜀 =
𝐶𝑟
1 + 𝑒𝑜
log
𝑃𝑐
𝜎𝑖
′ +
𝐶𝑐
1 + 𝑒𝑜
log
𝜎𝑓
′
𝜎𝑖
′
El esfuerzo inicial no necesariamente es el esfuerzo en sitio inicial debido a la carga gravitacional. En el
análisis multi-etapa, el cambio en deformaciones se calcula por cada etapa al usar el esfuerzo efectivo al
inicio de la etapa y el esfuerzo efectivo en el fin de la etapa.

29. Asentamiento secundario
𝑥Método estándar – Se asume que el asentamiento secundario
varia linealmente con el logaritmo de tiempo.
Δ𝜀𝑠 =
𝐶𝛼
1 + 𝑒𝑝
log
𝑡2
𝑡1
𝛿 = Δ𝑧 = 𝜀ℎ
𝛿𝑖 = 𝛿𝑖+1 + 𝜀𝑖ℎ𝑖

30. Asentamiento secundario
Para los materiales lineales y de Janbu, no hay una relación de
vacios asociado, por lo que en vez de 𝐶𝛼, el usuario debe colocar
el índice de compresión secundaria modificado o el índice de
compresión secundaria basada en deformaciones.
𝐶𝛼𝜀 =
𝐶𝛼
1 + 𝑒𝑝
⇒ Δ𝜀𝑠 = 𝐶𝛼𝜀 log
𝑡2
𝑡1

31. Asentamiento Secundario
Para llegar al fin de la consolidación primaria, se necesita asumir
un grado de consolidación.
Una consolidación primaria de 100% solo ocurre después de
tiempo infinito.
Por lo tanto un valor default es de una consolidación primaria de
95% se usa como el punto de arranque para la consolidación
secundaria donde el grado de consolidación es:
𝑈 = 1 −
𝑢𝑒
𝑢𝑒0

32. Asentamiento Secundario
𝑈 = 1 −
𝑢𝑒
𝑢𝑒0
𝑢𝑒 Presión de poro en exceso en el momento
𝑢𝑒0 Presión de poro en exceso al momento de la aplicación de
carga (si se aplicaron cargas diferentes en tiempos
diferentes, entonces este valor es la presión de poro máxima
excesiva).
El grado de consolidación es valido estrictamente para un material
lineal, sin embargo solo se usa como un estimado para la
consolidación secundaria, así que no es necesaria la precisión.

33. Asentamiento Secundario
El porcentaje de consolidación primaria en el cual se inicia la
consolidación secundaria.
No es realista que las capas de suelo sujetas a cambios de
esfuerzos a muy pequeños sufran de consolidación secundaria,
por lo tanto se debe obtener un esfuerzo mínimo para comenzar
la consolidación secundaria.
En Settle3 este es el 1% de un esfuerzo inicial debido a la
gravedad.

34. Referencias
La teoría detrás del cálculo de
Settle3 se tomo del PDF emitido por
Rocscience:
https://static.rocscience.cloud/assets/
verification-and-
theory/Settle3/Settle3-Theory-
Manual.pdf