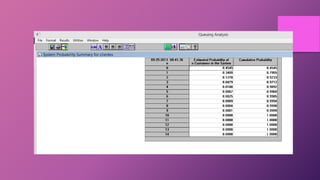
Este documento describe el sistema de colas M/M/C, donde las llegadas siguen un proceso de Poisson, los tiempos de servicio se distribuyen exponencialmente, y hay C servidores. Explica que la intensidad de tráfico debe ser menor que 1/C para alcanzar el estado estable, y presenta una aplicación numérica de un almacén con 2 cajeras.

1. Sistema de Colas M/M/C
Mendoza Heredia José Alfredo
ITIC
11121402
Investigación de Operaciones
Instituto Tecnológico
de Morelia
Morelia, Michoacán a 25 de septiembre de 2013

2. Sistema M/M/C (M/M/C)(DG/∞/∞)
(M/M/C)
• M = Descripción del proceso de llegada; Llegadas Markovianas.
• M = Distribución del tiempo de servicio; Servicio Markoviano.
• C = Número de servidores en el sistema.
(DG/∞/∞)
• DG = Disciplina General.
• ∞ = Capacidad del Sistema.
• ∞ = Tamaño de la población.

3. Con respecto a la notación de Kendall, para este
sistema se tienen las siguientes características:
 Se tiene un sistema de llegadas que se
producen según un proceso de Poisson de
razón λ, donde los tiempos entre llegadas
estarán distribuidos exponencialmente Exp(λ) o
Donde λ es el número medio de llegadas por
unidad de tiempo.
 Los tiempos entre servicios son distribuidos de
manera exponencial, Exp(µ) o Donde µ es el
número medio de paquetes que el servidor es
capaz de atender por unidad de tiempo.

4.  El número de servidores en el sistema de
denotará con la constante c .
 La capacidad del sistema es infinita, la
cual se puede omitir.
 La disciplina del sistema será FIFO, la
cual se puede omitir.
 Se tiene un estado de servicio igual a
uno, es decir una sola cola, el cual se
puede omitir también.
 Cuando c=1 medidas de rendimiento
igual a M/M/1

5. Intensidad de Tráfico/Estado Estable
Este sistema al igual que el sistema M/M/1 presenta
una capacidad del sistema infinita por lo cual se
establece una condición de no saturación para
alcanzar el estado estable, ya que de esta manera
se cuida que el número de paquetes no crezca
indefinidamente.
1
C

6. 1
0 !
)(
)1(!
1
0
c
n n
n
c
c
cc
c
P

7. cn
cn
P
n
n
c
n
P
,...,3,2,1
!
)(
0
cn
cccn
P
c
Pc
n
P
cc
,...3,2,1
)1(!
02
0
1

8. 2
0
)1(!
1
c
P
c
c
q
L
c
ss
WL
qs
LL
q
q
L
W
1
qs
WW

9. 0
)1(!
)(
)(
)1)(1(!
]1[)(1
)(
)1(0
)1(
0
t
ambas
para
c
Pc
tW
ccc
Pc
tW
tc
c
q
cctc
t




10. Aplicación
Un almacén tiene 2 cajeras que atienden a razón de 1.5 minutos por cliente
siguiendo una distribución exponencial. Los clientes llegan a este almacén
siguiendo una distribución de Poisson a razón de 30 por hora. Con esta
información calcular:
a) La intensidad del tráfico.
b) La probabilidad de que el sistema este sin ningún cliente.
c) El número promedio en la fila.
d) El tiempo promedio de espera en la cola.
e) El tiempo promedio de espera en el sistema.
f) Número promedio en el sistema.

11. Solución

12. Uso de Software WINQSB-Queuning Analysis