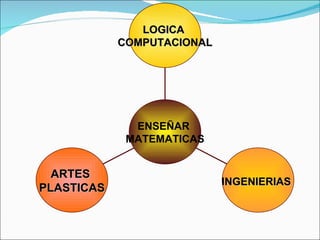
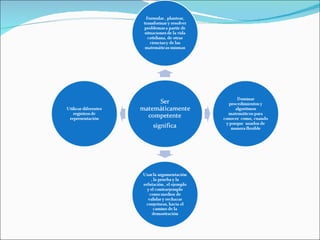
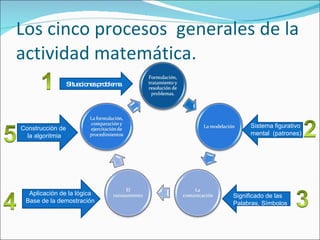
El documento describe los fundamentos de la enseñanza de las matemáticas, incluyendo tres paradigmas clave (medir, contar y ordenar) y el desarrollo de competencias matemáticas en los estudiantes. También discute métodos como utilizar contextos y problemas para generar conceptos matemáticos y desarrollar el pensamiento numérico, proporcional y de resolución de problemas en los estudiantes.

1. Desde el principio de los tiempos el hombre ha estado en busca de dar solución a tres paradigmas como son: Medir – Contar -Ordenar

2. Definamos Entonces Medir : comparar una cantidad con la unidad , para poder determinar cuantas veces aparece esta contenida en ella . Contar :Numerar las cosas como unidades. Ordenar :disponer de forma sistemática un conjunto de datos, a partir de un atributo determinado.

3. Por qué ? Enseñar Matemáticas . La Educación Matemática debe responder a nuevas demandas globales y nacionales, como la relacionada en educación para todos, la atención a la diversidad y a la interculturalidad y la formación de ciudadanos(nas) con las competencias necesarias para el ejercicio de sus derechos y deberes democráticos

4. ARTES PLASTICAS INGENIERIAS LOGICA COMPUTACIONAL ENSEÑAR MATEMATICAS

5. Desde inicios de la República hasta la década de los setenta la contribución de las matemáticas a fines de la educación y el desarrollo tecnológico del país . En principio de habló de un desarrollo netamente algorítmico y memorístico , principio que fué muy cuestionado ya que el desarrollo de un pensamiento lógico y preparación para la ciencia y la tecnología no son tareas de las matemáticas sino de todas las áreas de la educación básica y Media . La Búsqueda de la equidad hombre y mujer y resolver los problemas de su entorno (Cultural -Socio afectivo) Enseñando Matemáticas En Colombia

6. En competencias Se hace necesario pasar de una enseñanza orientada sólo hacia el logro de objetivos específicos relacionados con los contenidos del área y hacia la retención de dichos contenidos, a una enseñanza que se oriente a apoyar a los estudiantes en el desarrollo de competencias matemáticas, científicas, tecnológicas, lingüísticas y ciudadanas.

7. Competencias : conjunto de conocimientos, habilidades, actitudes, comprensiones y disposiciones cognitivas, socio afectivas y psicomotoras apropiadamente relacionadas entre sí para facilitar el desempeño flexible, eficaz y con sentido de una actividad en contextos relativamente nuevos y retadores .

8. Distingamos entonces.. Conocimiento Conceptual: Procedimiento teórico, producido por la actividad cognitiva.(se relaciona con la forma de saber y el saber por qué) Conocimiento Procedimental: Mas cercano a la acción y se relaciona con las técnicas y estrategias para representar conceptos y para transformar dichas representaciones con las habilidades y destrezas para elaborar, comparar y ejercitar algoritmos y para argumentar convincentemente.

10. Concluyamos Los dos tipos de conocimientos señalan derroteros para aproximarse a una interpretación enriquecida de la expresión ser matemáticamente competente. Algunos procesos generales presentes en la actividad matemática que explicitan lo que significa ser matemáticamente competente .

11. Los cinco procesos generales de la actividad matemática. Situaciones problema Sistema figurativo mental (patrones) Significado de las Palabras, Símbolos Aplicación de la lógica Base de la demostración Construcción de la algoritmia

12. Los cinco tipos de pensamiento matemático

14. Pensamiento numérico y sistemas numéricos Los procesos curriculares y orientar actividades en : Significado de los números y la numeración. Comprensión y significado de las operaciones y relaciones entre números y el desarrollo de diferentes técnicas de calculo y estimación.(magnitudes, cantidades discretas y continuas, medidas). Técnicas de conteo. (Evolución de los sistemas desde el indoarábigo ) en números Naturales-Enteros-Reales ...

15. Metodología de aplicación Ambientes Matemáticos Contextuales y Transversales

16. LA GENERACION DEL CONCEPTO En el proceso de Enseñanza aprendizaje de las matemáticas se debe tener en cuenta como principio fundamental la Construcción del concepto en nuestro Estudiante

17. Porque Interiorizar el Concepto? Cuando se aprende el concepto mediante la aplicación del conocimiento en el contexto , el estudiante reafirma su saber (conceptual) con la aplicación (Saber practico ), encontrando allí una coherencia clara sobre lo que piensa, procesa y lo que finalmente obtuvo

18. Vemos entonces que nuestro estudiante ya inicio la etapa de relacion entre el saber y saber hacer.

19. Aspectos Metodológicos La metodología de enseñanza de las matemáticas implementada en la enseñanza debe involucrar las siguientes concepciones : Desarrollar habilidades de tipo cognitivo en el estudiante Desarrollar habilidades de tipo Argumentativo y Propositivo en el estudiante.

20. Como se desarrolla dicha metodología El Docente debe tener claro los siguientes aspectos : Utilizar el modelo contextual del estudiante (es decir pensar, vivir e intentar sentir como el estudiante) Diseñar un currículo que se ajuste a el contexto del estudiante. Ajustar cada Eje temático a un Proyecto de manera transversal. Iniciar cada temática con preguntas problematizadoras-generadoras o Esenciales

21. Modelo Contextual El Docente debe desarrollar actividades que involucren directamente el sentir, el pensar y el quehacer de los estudiantes. (Ejemplo de ello ;preparar temas utilizando el tipo de música que la mayoría de los estudiantes les gusta)

22. Ejemplo de Aplicación (Utilizacion de algunos tipos de pensamientos) Los Estudiantes de Grado 6° de Determinada Institución inician sus labores académicas del año curricular. Su profesor plantea una pregunta : “ El mundo que nos Rodea?” Inicia preguntándole a cada uno de los estudiantes y que ellos vayan mencionando un componente relacionado a esta pregunta .

23. Las respuestas de los estudiantes Algunos estudiantes responden : Animales , casas, agua montañas,edificios,personas,automoviles, entre otros . La aplicación de las respuestas a el contexto inmediato y transversal . Observemos y analicemos cada una de sus respuestas

24. Análisis de las Respuestas Animales :Esta respuesta es transversal a el área de ciencias naturales. Casas Montañas- Edificios : Esta respuesta es transversal a el área de ciencias Sociales Personas : Transversal a todas la áreas. Automóviles :transversal a ciencias Naturales-Sociales

25. Digamos Que. Entonces el estudiante relaciona las respuestas de la pregunta esencial con varias áreas de su grado .

26. Resolución de Problemas a partir de preguntas La pregunta generadora –Esencial o Problemica conlleva a que se puedan formular diferentes tipos de problemas que el estudiante puede resolver desde su habilidad conceptual .

27. Un ejemplo para aportar en el desarrollo del pensamiento numérico es aquel donde el estudiante observa una operación .Luego el procede a resolverla sin hacer el cálculo en forma manual . EJEMPLO :Observa con detenimiento cada una de las siguientes operaciones y responde en cual de ellas se obtiene un mayor resultado , y en cual el resultado es menor , además ordene los resultados de mayor a menor.

28. Ejemplo1 10+20= 45-35 = 12*2 = Obtenga los resultados en forma mental ,luego ordena de mayor a menor

29. Resolviendo diversos tipos de problemas (composición) A una fiesta llegan 7 niños y 4 niñas, al iniciar el baile ,cada uno de los niños elige una niña para bailar, entonces : ¿Cuántos niños quedan sin pareja? ¿Cuánto es el total de niños y niñas que asisten a la fiesta? ¿Cuántas niñas quedan sin parejo?

30. Transformación El proceso de transformación contiene las etapas : (inicial –proceso –resultado transformado ). Un ejemplo clásico de ello podría ser : Carlitos juega con Andrés a las canicas (Al iniciar el juego Carlitos tenia 25 canicas y Andrés 18), al terminar de jugar Carlitos termina con 40 Canicas (Explique que pasó con las canicas de Andrés y Carlitos)

31. Proporcionalidad El concepto de proporción fundamenta en el estudiante la relación entre dos variables en forma de razón . Ejemplo :un niño en su juego de carritos de la formula 1, quiere medir los tiempos de Juan Pablo Montoya en su play, en la sesión de entrenamiento y los registra entonces en la siguiente atabla :

32. Según los tiempos de duración ,completa la siguiente tabla . Aclarando que los tiempos se mantienen. Numero de Giros a la pista 10 20 30 40 50 Tiempo (mins) 20 60 100

33. Ejemplificación (Cuarto –Quinto ) Es importante inculcar en el estudiante que un número se puede representar de diferentes maneras. La inclusión de este ejemplo se encuentra directamente relacionada con el pensamiento de tipo numérico.

34. Nota :el número es una representación por convención de una cantidad . Ejemplo 1 Relaciona con una línea los gráficos que corresponden al mismo número .

35. Resolviendo diferentes tipos de problemas (comparación e igualación) La idea es que el estudiante compare dos o más cantidades y que saque una conclusión de ello . Ejemplo 1: Carlitos tiene 10 años y Andrés tiene 5 años mas que Carlitos . ¿Cuántos años tiene Andrés ?

36. Ejemplo 2: Carolina tiene 10 cds de música moderna, mientras que Mariana tiene 4 mas que Carolina, pero Sofía tiene 2 mas que Carolina y 2menos que Mariana. ¿Cuántos cds tiene entonces Mariana ? ¿Cuantos cds tiene entonces Sofía?

37. Problemas de Igualdad La relación ser igual a otro ,debe despertar en el niño la capacidad de saber cuando un elemento presenta las mismas propiedades que otro y cuando no. Aparece una comparación intrínseca del lenguaje entre lo que se denomina sinónimo y antónimo. Ejemplo 1. Sofía tiene 12 muñecas de pelo rubio, Andrea tiene 5 de cabello rubio y 7 de con cabello de otro color, ¿la cantidad de muñecas que tiene Carolina es entonces igual diferente a la que tiene Sofía .?

38. BIBLIOGRAFIA MEN :Ministerio de Educación Nacional . Estándares Básicos de Competencias en Lenguaje, Matemáticas, Ciencias y Ciudadanas. Experiencias significativas.