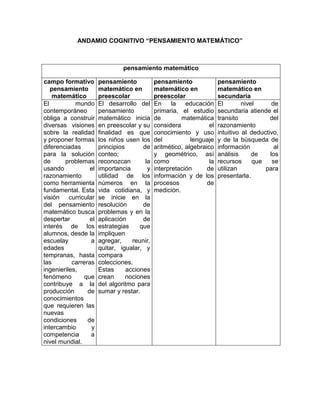
El documento describe cómo el pensamiento matemático se desarrolla a lo largo de las diferentes etapas educativas, desde preescolar hasta secundaria. En preescolar, el objetivo es que los niños usen principios de conteo y reconozcan números en la vida cotidiana. En primaria, se estudian conceptos como lenguaje aritmético, álgebra y geometría. En secundaria, el enfoque cambia del razonamiento intuitivo al deductivo, y de encontrar a analizar información. El documento también destaca la importancia de despertar

1. ANDAMIO COGNITIVO “PENSAMIENTO MATEMÁTICO”
pensamiento matemático
campo formativo pensamiento pensamiento pensamiento
pensamiento matemático en matemático en matemático en
matemático preescolar preescolar secundaria
El mundo El desarrollo del En la educación El nivel de
contemporáneo pensamiento primaria, el estudio secundaria atiende el
obliga a construir matemático inicia de matemática transito del
diversas visiones en preescolar y su considera el razonamiento
sobre la realidad finalidad es que conocimiento y uso intuitivo al deductivo,
y proponer formas los niños usen los del lenguaje y de la búsqueda de
diferenciadas principios de aritmético, algebraico información al
para la solución conteo; y geométrico, así análisis de los
de problemas reconozcan la como la recursos que se
usando el importancia y interpretación de utilizan para
razonamiento utilidad de los información y de los presentarla.
como herramienta números en la procesos de
fundamental. Esta vida cotidiana, y medición.
visión curricular se inicie en la
del pensamiento resolución de
matemático busca problemas y en la
despertar el aplicación de
interés de los estrategias que
alumnos, desde la impliquen
escuelay a agregar, reunir,
edades quitar, igualar, y
tempranas, hasta compara
las carreras colecciones.
ingenieriles, Estas acciones
fenómeno que crean nociones
contribuye a la del algoritmo para
producción de sumar y restar.
conocimientos
que requieren las
nuevas
condiciones de
intercambio y
competencia a
nivel mundial.

2. Elabore un texto, que permita dar cuenta de la funcionalidad de las matemáticas
en la vida ¿sirven para algo o habrá que replantear la importancia de esta ciencia
en la educación? Existe diferencias entre la habilidad para resolver problemas de
forma oral y de forma escrita. De manera similar reflexione acerca de si usted, en
sus clases, permite a sus alumnos resolver los problemas “como quieran” así
como de la importancia de considerar los saberes previos y las estrategias de
resolución de los alumnos en la clase.la funcionalidad de las matemáticas en la
vida.
LA FUNCIONALIDAD DE LAS MATEMÁTICAS EN LA VIDA
Las matemáticas empiezan a dar vida desde nuestros primeros años de vida; ya
que en nuestras actividades cotidianas las empleamos de forma espontánea.
El ambiente natural, cultural y social en que vivimos nos provee de experiencias
que, de manera espontánea nos lleva a realizar problemas de conteo, que son una
herramienta básica del pensamiento matemático.
Por muchos años los contenidos se han venido trabajado de manera aislada. Es
decir, fuera de un contexto que permita al alumno descubrir su significado, sentido
y funcionalidad.
Además, con frecuencia, se nos dificulta como plantear un problema, ya que no
permitimos que los alumnos se enfrenten realmente a ellos. Se les dice como
resolverlo o se les propone problemas de forma mecánica, pero no se estimula la
búsqueda personal y la creación de procedimientos propios.
Cuando los alumnos tienen libertad para buscar la manera de resolver un
problema, encuentran al menos una forma de aproximarse al resultado. Esto, a su
vez, puede generar en el grupo una valiosa diversidad de procedimientos.
Tiene un gran valor didáctico, que los alumnos conozcan las diferente formas de
solución que encuentran sus compañerospara un mismo problema, existen varias
formas, algunos más largos y complicados que otros, pero lo importante es
acercarse a la solución. Esto también permite percatarse de sus errores y favorece
que, por si mismos, valoren sus resultados.
Cuando los alumnos logran comprender el procedimiento que otros siguieron para
resolver algún problema, pueden probarlo en otras situaciones. Probar,
equivocarse, volver a probar hasta lograr una solución, propicia que los niños
avancen en su aprendizaje adquieran confianza en el manejo de sus

3. conocimientos, reconozcan su validez y los utilicen para resolver las diversas
situaciones a las que se enfrentan en la vida cotidiana y en la escuela.
Otro de los aspectos que se debe tomar en cuentas, son los conocimientos
previos y los procedimientos iniciales en la resolución de problemas deben ser, el
punto de partida para avanzar en la construcción de nuevos conocimientos.
La lectura de Rosbi y las matemáticas de cortina Morfín, JoséLuis es una
evidencia de que es posible cambiar algunos aspectos en la enseñanza de las
matemáticas, si nosotros les damos confianza y seguridad a los alumnos, tendrán
la capacidad de resolver los problemas matemáticos, estamos contribuyendo de
que los alumnos sean más analíticos, expresivos y finalmente hacerles ver de que
las matemáticas las usamos a diario y de que si sirven.
Se pretende que los niños de preescolar (y de todos los que cursan la educación
básica) es que el conocimiento que adquieran les sea significativo; lo cual quiere
decir que en una situación donde tenga sentido usar ese conocimiento lo
recuerden y lo empleen para resolver, que es equivalente a lograr el desarrollo de
competencias.