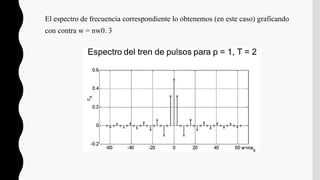
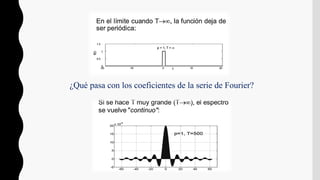
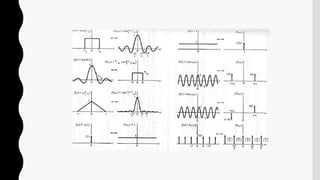
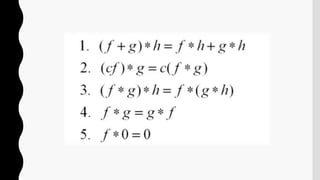La convolución es una operación matemática que combina dos funciones en una tercera función. Se define como la integral del producto de las funciones después de desplazar una de ellas. Tiene aplicaciones en estadística, teoría de probabilidad, óptica, acústica e ingeniería. La transformada de Fourier de una convolución es el producto punto a punto de las transformadas individuales.