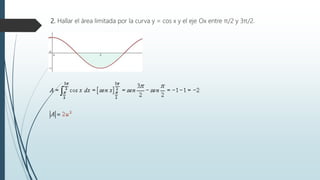
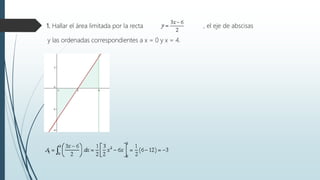
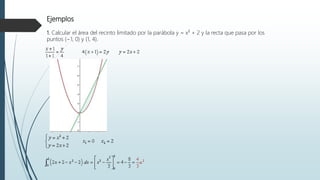
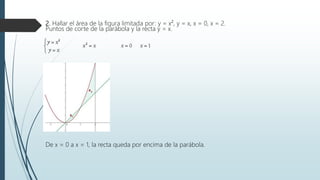
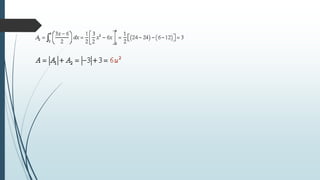Este documento explica el concepto de integral definida y sus propiedades. La integral definida representa el área limitada entre una función, el eje horizontal y los límites del intervalo. El documento también cubre cómo calcular áreas limitadas por funciones, entre dos funciones, y volúmenes de revolución utilizando integrales definidas.

1. INTEGRAL DEFINIDA
Garrido Miguel
C.I: 28.704.718
INSTITUTO UNIVERSITARIO POLITÉCNICO
SANTIAGO MARIÑO
SEDE BARCELONA – ESTADO ANZOÁTEGUI
BARCELONA, MARZO 2019

2. La integral definida es un concepto utilizado para determinar el valor de las áreas
limitadas por curvas y rectas. Dado el intervalo [a, b] en el que, para cada uno de sus
puntos x, se define una función f (x) que es mayor o igual que 0 en [a, b], se llama
integral definida de la función entre los puntos a y b al área de la porción del plano
que está limitada por la función, el eje horizontal OX y las rectas verticales de
ecuaciones x = a y x = b.
Introducción

3. Integral Definida
Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área
limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.

4. La integral definida se representa por:
∫ es el signo de integración.
a límite inferior de la integración.
b límite superior de la integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.

5. Propiedades de la Integral Definida
1. El valor de la integral definida cambia de signo si se permutan los límites de integración.
2. Si los límites que integración coinciden, la integral definida vale cero.

6. 3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone
como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].
4. La integral definida de una suma de funciones es igual a la suma de integrales·
5. La integral del producto de una constante por una función es igual a la
constante por la integral de la función.

7. Función Integral
Sea f(t) una función continua en el intervalo [a, b]. A partir de esta función se define la función
integral:
que depende del límite superior de integración.
Para evitar confusiones cuando se hace referencia a la variable de f, se la llama t, pero si la
referencia es a la variable de F, se la llama x.

8. Geométricamente la función integral, F(x), representa el área del recinto
limitado por la curva y = f(t), el eje de abscisas y las rectas t = a y t = x.
A la función integral, F(x), también se le llama función de áreas de f en el intervalo [a, b].

9. Área I
Caso 1
Área entre una función positiva y el eje de abscisas
Si la función es positiva en un intervalo [a, b] entonces la gráfica de la
función está por encima del eje de abscisas. El área de la función viene
dada por:
Para hallar el área seguiremos los siguientes pasos:
1º Se calculan los puntos de corte con con el eje OX, haciendo f(x) = 0 y
resolviendo la ecuación.
2º El área es igual a la integral definida de la función que tiene como límites de
integración los puntos de corte.

10. 1. Calcular el área del recinto limitado por la curva y = 9 − x² y el eje OX.
En primer lugar hallamos los puntos de corte con el eje OX para representar la
conocer los límites de integración.
Como la parábola es simétrica respecto al eje OY, el área será igual al doble del área
comprendida entre x = 0 y x = 3.

11. 2. Calcular el área limitada por la curva xy = 36, el eje OX y las rectas: x = 6, x = 12.
Ejemplo:

12. 3. Calcular el área del triángulo de vértices A(3, 0), B(6, 3), C(8, 0).
Ecuación de la recta que pasa por AB:
Ecuación de la recta que pasa por BC:

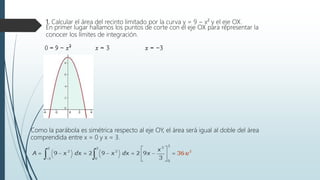
14. Caso 2: Área entre una función negativa y el eje de abscisas
Si la función es negativa en un intervalo [a, b] entonces la gráfica de la función está por debajo
del eje de abscisas. El área de la función viene dada por:
1. Calcular el área del recinto limitado por la curva y = x² − 4x y el eje OX

15. 2. Hallar el área limitada por la curva y = cos x y el eje Ox entre π/2 y 3π/2.

16. Caso 3: La función toma valores positivos y negativos
En ese caso el el recinto tiene zonas por encima y por debajo del eje de abscisas. Para calcular
el área de la función seguiremos los siguientes pasos:
1º Se calculan los puntos de corte con con el eje OX, haciendo f(x) = 0 y resolviendo la ecuación.
2º Se ordenan de menor a mayor las raíces, que serán los límites de integración.
3º El área es igual a la suma de las integrales definidas en valor absoluto de cada intervalo.

17. 1. Hallar el área limitada por la recta , el eje de abscisas
y las ordenadas correspondientes a x = 0 y x = 4.

19. 2. Calcular el área de la región del plano limitada por el círculo x² + y² = 9.
Ejemplos
El área del círculo es cuatro veces el área encerrada en el primer cuadrante y los ejes de
coordenadas.

20. Hallamos los nuevos límites de integración.

21. Área II
Área comprendida entre dos funciones
El área comprendida entre dos funciones es igual al área de la función que
está situada por encima menos el área de la función que está situada por
debajo.

22. Ejemplos
1. Calcular el área del recinto limitado por la parábola y = x² + 2 y la recta que pasa por los
puntos (−1, 0) y (1, 4).

23. 2. Hallar el área de la figura limitada por: y = x², y = x, x = 0, x = 2.
Puntos de corte de la parábola y la recta y = x.
De x = 0 a x = 1, la recta queda por encima de la parábola.

24. De x = 1 a x = 2, la recta queda por debajo de la parábola.

25. Volúmen de una función
El volumen del cuerpo de revolución engendrado al girar la curva f(x) alrededor del eje OX
y limitado por x = a y x = b, viene dado por:

26. Ejemplos:
1. Hallar el volumen del tronco de cono engendrado por la rotación alrededor OX del área
limitada por y = 6 − x, y = 0, x = 0, x = 4.

27. 2. Calcular el volumen engendrado por una semionda de la sinusoide y = sen x, al girar
alrededor del eje OX.

28. 3. Hallar el volumen del cuerpo revolución engendrado al girar alrededor del eje OX, la región
determinada por la función f(x) = 1/2 + cos x, el eje de abscisas y las rectas x = 0 y x = π.

29. 4. Hallar el volumen engendrado por el círculo x² + y² − 4x = −3 al girar alrededor del eje OX.
El centro de la circunferencia es C(2, 0) y el radio r = 1.
Puntos de corte con el eje OX:

31. Conclusión
El concepto de integral tuvo su origen histórico en la necesidad de resolver
problemas concretos como: cálculo de área limitada por dos
curvas, longitudes de arcos, volúmenes, trabajo, velocidad, momentos de
inercia, etc.; todos estos cálculos se pueden realizar mediante la integral
definida.

32. Bibliografía
https://es.slideshare.net/marcounmsm28/concepto-de-integral-definida-1
https://www.ecured.cu/Integral_definida#Ejemplo
https://www.vitutor.com/integrales/definidas/integral_definida.html
https://www.ecured.cu/Integral_definida#Aplicaciones