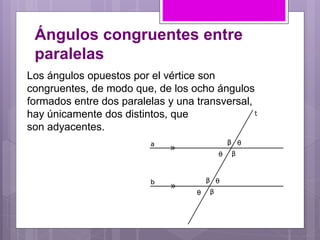
Este documento describe los diferentes tipos de ángulos que se forman entre dos rectas paralelas y una transversal, incluyendo ángulos correspondientes, alternos, externos e internos. También cubre teoremas relacionados como los de Desargues y Tales, así como la noción de triángulos semejantes.

1. Cristina Ramírez

2. Ángulos entre paralelas
 En geometría euclidiana, los ángulos entre
paralelas son los ocho ángulos formados por
dos rectas paralelas y una transversal a ellas.
Se clasifican según su congruencia.

3.  Ángulos Correspondientes:
Las parejas de ángulos: <1 y <5; <2 y <6; <4 y <8; <3 y
<7 se llaman ángulos correspondientes, y son
congruentes.
 Ángulos Alternos:
Son los que "fuera" de las paralelas fueran a distinto lado
de ellas y a distinto lado de la transversal. Son iguales
entre sí; es decir miden lo mismo.
 Ángulos Externos:
Las parejas de ángulos: <1 y <7; <2 y <8 se
llaman ángulos alternos externos, y son congruentes.
 Ángulos Internos:
Las parejas de ángulos: <4 y <6; <3 y <5 se
llaman ángulos alternos internos, y son congruentes.

4. Ángulos congruentes entre
paralelas
Los ángulos opuestos por el vértice son
congruentes, de modo que, de los ocho ángulos
formados entre dos paralelas y una transversal,
hay únicamente dos distintos, que
son adyacentes.

5. Teoremas y resultados
relacionados
 La noción de ángulos correspondientes es la base
de numerosos ejemplos y teoremas fundamentales de
la geometría, presente en los cursos de enseñanza
media de las matemáticas. Es un resultado geométrico
intuitivo conocido y manejado desde la antigüedad, de
manera tanto práctica como teórica, si bien es la
ciencia griega, y en particular Euclides,
en los Elementos (siglo III a.C.), quienes formalizan los
conceptos y las nociones de un modo que ha
permanecido casi sin variaciones hasta nuestros días.

6. Teorema de Desargues
 En geometría proyectiva, el teorema de Desargues, llamado así en honor
a Gérard Desargues, expone:

 Considere los triángulos ABC y DEF. El que los triángulos sean proyectivos
desde un punto significa que las rectas AD, BE y CF concurren en un mismo
punto O. De modo parecido, el que los triángulos sean proyectivos desde una
recta significa que los pares de lados (AB, DE), (BC, EF) y (AC, DF) se cortan
respectivamente sobre una misma recta r.
 Al punto O se le llama centro de perspectiva y a la recta r, eje de
perspectiva.
En el plano proyectivo, dos triángulos son proyectivos desde un
punto si y sólo si son proyectivos desde una recta.

7. Teorema de Tales
 Teorema primero
Si en un triángulo se traza una línea paralela a
cualquiera de sus lados, se obtiene un triángulo
que es semejante al triángulo dado.
 Teorema segundo
Sea B un punto de la circunferencia de
diámetro AC, distinto de A y de C. Entonces el
triángulo ABC, es un triángulo rectángulo.

8. Triángulos Semejantes
 Es la variación en tamaño entre dos objetos o
cuerpos pero sus formas son idénticas. Se
dice que dos figuras geométricas
son semejantes si tienen la misma forma pero
sus tamaños son diferentes. Por ejemplo, dos
mapas a escalas distintas son semejantes,
pues la forma del o los contenidos no cambia,
pero si el tamaño.