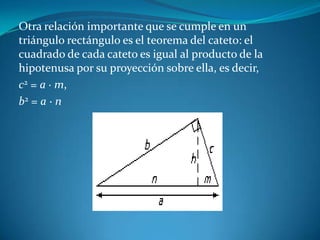
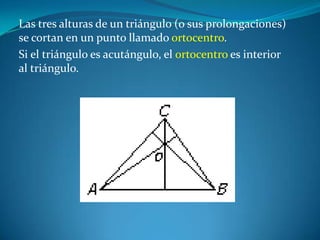
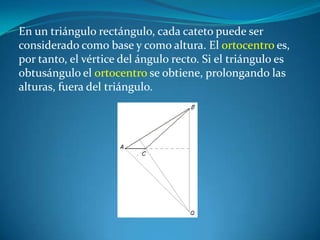
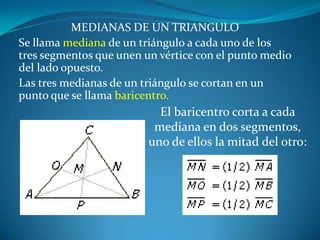
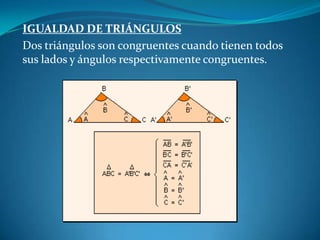
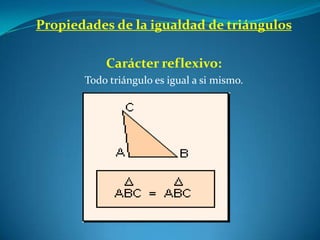
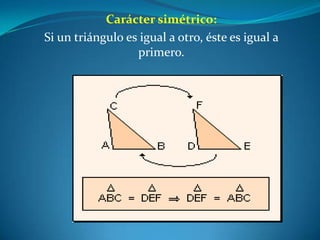
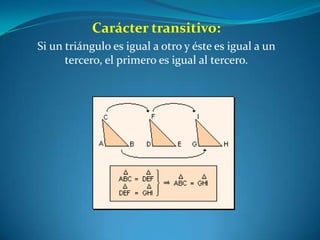
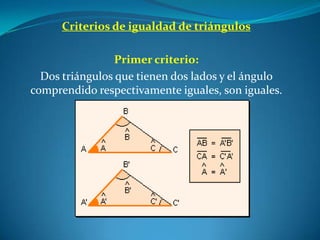
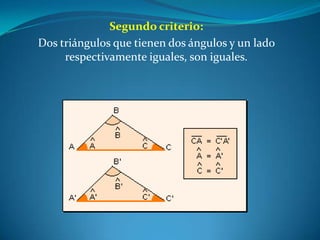
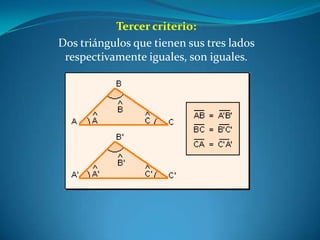
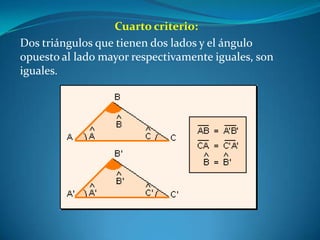
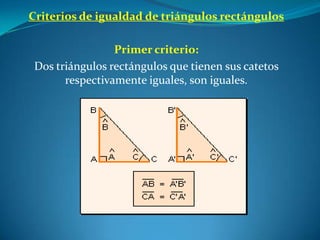
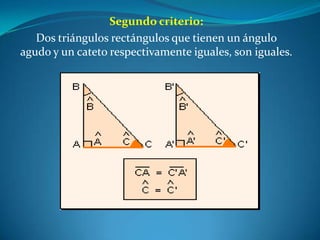
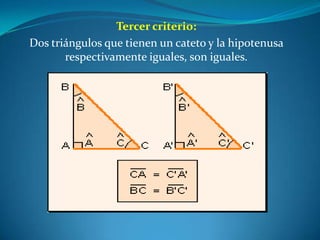
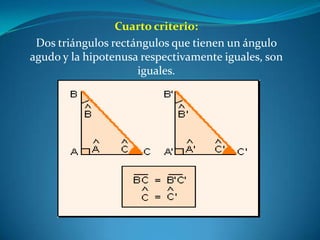
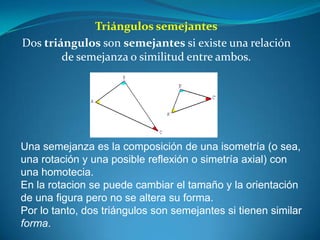
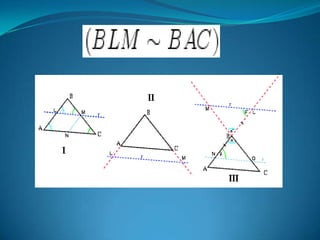
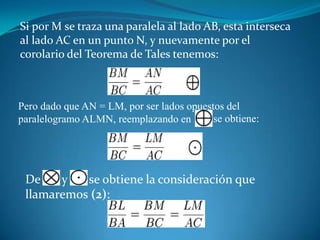
Este documento describe las propiedades de los triángulos, incluyendo definiciones de tipos de triángulos, teoremas sobre lados, ángulos y áreas, y criterios para determinar la igualdad y semejanza de triángulos. Explica conceptos como catetos, hipotenusa, alturas, medianas, circunferencias inscritas y circunscritas, y presenta fórmulas como la de Pitágoras y Herón.

1. OCTAVO GRADOUNIDAD No 3 MIDAMOS Y CONSTRUYAMOS CON TRIANGULOS. Por: Vidal Cruz

2. TRIÁNGULOS. DEFINICIÓN: El triángulo es un polígono de tres lados que se cortan entre sí. Según la longitud de sus lados, los triángulos se clasifican en equiláteros,si sus tres lados son iguales, isósceles, si tienen dos lados iguales, y escalenos, si los tres lados son distintos.

3. La suma de los tres ángulos de un triángulo es 180º. Dos de los ángulos son, necesariamente, agudos. El tercero puede ser también agudo, o bien recto u obtuso. Si los tres ángulos son agudos el triángulo se llama acutángulo, si tiene un ángulo recto, rectángulo y obtusángulo si el mayor de sus ángulos es obtuso.

4. TRIANGULOS RECTANGULOS. Los triángulos rectángulos cumplen una serie de relaciones métricas importantes entre sus lados. Los lados de un triángulo rectángulo que forman el ángulo recto, b y c, se llaman catetos y el tercer lado, a, (opuesto al ángulo recto) es la hipotenusa. El teorema de Pitágoras relaciona los dos catetos y la hipotenusa: en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos: a2 = b2 + c2

5. Otra relación importante que se cumple en un triángulo rectángulo es el teorema del cateto: el cuadrado de cada cateto es igual al producto de la hipotenusa por su proyección sobre ella, es decir, c2 = a ·m, b2 = a · n

6. ALTURAS DE UN TRIANGULO Se llama base de un triángulo a cualquiera de sus lados. El segmento perpendicular desde un vértice a la base opuesta o a su prolongación se llama altura. Un triángulo tiene, pues, tres bases a, b, c, y las tres alturas correspondientes, ha, hb y hc. En un triángulo rectángulo el cuadrado de la altura sobre la hipotenusa es igual al producto de los dos segmentos en que la divide: h2 = m ·n Esta relación se conoce como teorema de la altura.

7. Las tres alturas de un triángulo (o sus prolongaciones) se cortan en un punto llamado ortocentro. Si el triángulo es acutángulo, el ortocentro es interior al triángulo.

8. En un triángulo rectángulo, cada cateto puede ser considerado como base y como altura. El ortocentro es, por tanto, el vértice del ángulo recto. Si el triángulo es obtusángulo el ortocentro se obtiene, prolongando las alturas, fuera del triángulo.

9. MEDIANAS DE UN TRIANGULO Se llama mediana de un triángulo a cada uno de los tres segmentos que unen un vértice con el punto medio del lado opuesto. Las tres medianas de un triángulo se cortan en un punto que se llama baricentro. El baricentro corta a cada mediana en dos segmentos, uno de ellos la mitad del otro:

10. CIRCUNFERENCIA INSCRITA. Las bisectrices de los tres ángulos de un triángulo se cortan en un punto que se llama incentro porque es el centro de la circunferencia inscrita que es tangente a los tres lados del triángulo. Ésta es la mayor circunferencia contenida en el triángulo. Para dibujar las bisectrices, es necesario medir cuántos grados tiene cada uno de los ángulos del triángulo, luego a esta cantidad se le saca mitad y se dibuja una recta dividiendo el ángulo en dos partes iguales.

11. CIRCUNFERENCIAS EXINSCRITAS La bisectriz interior de un ángulo se corta con las dos bisectrices exteriores de los otros dos ángulos en un punto llamado exincentro, y que es centro de una circunferencia (exinscrita) tangente a un lado y a la prolongación de los otros dos. Un triángulo tiene, pues, tres circunferencias exinscritas.

12. CIRCUNFERENCIA CIRCUNSCRITA. Las mediatrices de los lados de un triángulo se cortan en un punto llamado circuncentro porque es centro de la circunferencia circunscrita que pasa por los tres vértices del triángulo. Esta es la menor circunferencia que contiene al triángulo. AREA DE UN TRIANGULO El área de un triángulo de lados a, b, c, y alturas correspondientes ha, hb y hc es: A = (1/2)a ·ha = (1/2)b · hb = (1/2)c · hc

13. Si se conocen las longitudes de los tres lados, a, b, c, el área se puede calcular mediante la siguente fórmula, llamada fórmula de Herón: en donde p = (a + b + c)/2 es el semiperímetro del triángulo.

14. IGUALDAD DE TRIÁNGULOS Dos triángulos son congruentes cuando tienen todos sus lados y ángulos respectivamente congruentes.

15. Sólo es necesario verificar que ciertos elementos sean congruentes para que dos triángulos sean iguales, por lo que se definen 4 criterios de igualdad de triángulos. A partir de los criterios de igualdad anteriores derivan los criterios de igualdad de triángulos rectángulos. La igualdad de triángulos cumple las propiedades reflexiva, simétrica y transitiva.

16. Propiedades de la igualdad de triángulos Carácter reflexivo: Todo triángulo es igual a si mismo.

17. Carácter simétrico: Si un triángulo es igual a otro, éste es igual a primero.

18. Carácter transitivo: Si un triángulo es igual a otro y éste es igual a un tercero, el primero es igual al tercero.

19. Criterios de igualdad de triángulos Primer criterio: Dos triángulos que tienen dos lados y el ángulo comprendido respectivamente iguales, son iguales.

20. Segundo criterio: Dos triángulos que tienen dos ángulos y un lado respectivamente iguales, son iguales.

21. Tercer criterio: Dos triángulos que tienen sus tres lados respectivamente iguales, son iguales.

22. Cuarto criterio: Dos triángulos que tienen dos lados y el ángulo opuesto al lado mayor respectivamente iguales, son iguales.

23. Criterios de igualdad de triángulos rectángulos Primer criterio: Dos triángulos rectángulos que tienen sus catetos respectivamente iguales, son iguales.

24. Segundo criterio: Dos triángulos rectángulos que tienen un ángulo agudo y un cateto respectivamente iguales, son iguales.

25. Tercer criterio: Dos triángulos que tienen un cateto y la hipotenusa respectivamente iguales, son iguales.

26. Cuarto criterio: Dos triángulos rectángulos que tienen un ángulo agudo y la hipotenusa respectivamente iguales, son iguales.

27. Triángulos semejantes Dos triángulos son semejantes si existe una relación de semejanza o similitud entre ambos. Una semejanza es la composición de una isometría (o sea, una rotación y una posible reflexión o simetría axial) con una homotecia. En la rotacion se puede cambiar el tamaño y la orientación de una figura pero no se altera su forma. Por lo tanto, dos triángulos son semejantes si tienen similar forma.

28. En el caso del triángulo, la forma sólo depende de sus ángulos (no así en el caso de un rectángulo, por ejemplo, donde uno de sus ángulos es recto pero cuya forma puede ser más o menos alargada, es decir que depende del cociente base / altura). Se puede simplificar así la definición: dos triángulos son semejantes si sus ángulos son iguales dos a dos. En la figura, los ángulos correspondientes son A = A', B = B' y C = C'. Para denotar que dos triángulos ABC y DEF son semejantes se escribe ABC ~ DEF, donde el orden indica la correspondencia entre los ángulos: A, B y C se corresponden con D, E y F, respectivamente.

29. Una similitud tiene la propiedad (que la caracteriza) de multiplicar todas las longitudes por un mismo factor. Por lo tanto las razones longitud imagen / longitud origen son todas iguales, lo que da una segunda caracterización de los triángulos semejantes: Dos triángulos son semejantes si las razones de los lados correspondientes son congruentes.

30. Ecuación Se reúnen estas dos propiedades equivalentes en la siguiente ecuación: Corolarios 1. Todos los triángulos equiláteros son semejantes. 2. Si dos triángulos tienen dos ángulos iguales, los terceros también son iguales.

31. Propiedades de la semejanza Propiedad reflexiva, refleja o idéntica Todo triángulo es semejante a sí mismo. Propiedad idéntica o simétrica Si un triángulo es semejante a otro, aquel es semejante al primero. Propiedad transitiva Si un triángulo es semejante a otro, y éste a su vez es semejante a un tercero, el primero es semejante al tercero. Estas tres propiedades implican que la relación de semejanza entre dos triángulos es una relación de equivalencia.

32. Teorema de Thales Un caso particular es el que se da en el teorema de Thales, donde los triángulos tienen dos lados (vistos como rectas) comunes: (CA) = (CA') y (CB) = (CB'), y los lados restantes son dos catetos paralelos: (AB) // (A'B'). Triángulos semejantes según el teorema de Thales Los lados son así paralelos dos a dos y, por lo tanto, definen ángulos iguales. Por ello, los triángulos CAB y CA'B' son semejantes (de hecho son homotéticos), lo que implica la igualdad de los cocientes:

33. Otro teorema famoso de la geometría, el teorema de Pitágoras, es también una consecuencia inmediata de la doble caracterización de los triángulos semejantes. Teorema fundamental de la semejanza de triángulos Toda paralela a un lado de un triángulo que no pase por el vértice opuesto, determina con las rectas a las que pertenecen los otros dos lados, un triángulo semejante al dado. H) ABC; r || AC r corta AB en L r corta BC en M

35. Podrán presentarse 3 casos: I - r corta a los lados AB y BC por puntos interiores a ellos. Haremos una primera consideración, referida a los ángulos, y la llamaremos (1): Por otra parte, en virtud del corolario del Teorema de Tales se tiene: por carácter reflejo por ser correspondientes entre r || BC, secante AB por ser correspondientes entre r || BC, secante AC

36. Si por M se traza una paralela al lado AB, esta interseca al lado AC en un punto N, y nuevamente por el corolario del Teorema de Tales tenemos: Pero dado que AN = LM, por ser lados opuestos del paralelogramo ALMN, reemplazando en se obtiene: De y se obtiene la consideración que llamaremos (2):

37. Luego de (1) y (2), resulta: por definición de semejanza. II - r corta a las rectas de los lados AB y BC por puntos exteriores a ellos, sobre las semirrectas de origen B que los contienen. Consideramos BLM como si fuera el triángulo dado, y BAC el triángulo nuevo, y por el caso I de la demostración, es: por carácter simétrico.

38. III - r corta a las rectas de los lados AB y BC en puntos que pertenecen a las semirrectas opuestas a las que sirven de sostén a dichos lados. Sobre la semirrecta de origen B que contiene al punto A, se construye BN=BL y por el extremo N del segmento construido, una paralela a AC (s) que corta la recta de BC por O. Quedan entonces por el caso I, semejanza que llamaremos

39. Teniendo en cuenta los triángulos BNO y BLM, se observa: BN=BM por construcción α=α' por ser opuestos por el vértice. β=β' por ser alternos internos entre r || s, secante MN Y siendo BNO=BLM es BNO ~ BLM por el primer corolario de la definición. De y , y por carácter transitivo: BAC ~ BLMBLM ~ BAC

40. TEOREMA DE PITÁGORAS Teorema de Pitágoras, teorema que relaciona los tres lados de un triángulo rectángulo, y que establece que el cuadrado del lado mayor (hipotenusa) es igual a la suma de los cuadrados de los otros dos lados (catetos). El teorema de Pitágoras permite calcular uno de los lados de un triángulo rectángulo si se conocen los otros dos. Así, permite calcular la hipotenusa a partir de los dos catetos: o bien, calcular un cateto conocidos la hipotenusa y el otro cateto:

41. Ejemplo 1: Un triángulo rectángulo miden 4 cm. de base y 3 cm. de alto. Encuentre el valor de la hipotenusa. SOLUCIÓN: Fórmula a utilizar: a2 = b2 + c2 b = base c = altura a = hipotenusa = ? a2 = (4) 2 + (3)2 a2 = 16 + 9 a2 = 25 a = √25 a = 5 Por lo tanto la hipotenusa será igual a 5 cm. a c b