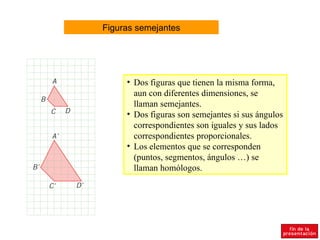
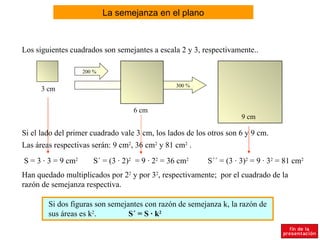
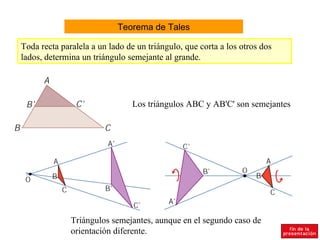
El documento resume conceptos básicos de geometría del plano como ángulos complementarios y suplementarios, igualdad de ángulos, suma de los ángulos interiores de triángulos y polígonos, mediatrices, bisectrices, teorema de Tales, circuncentro, incentro, baricentro, ortocentro, figuras semejantes, criterios de semejanza de triángulos y teorema de Pitágoras.

1. XEOMETRÍA DO PLANO

2. Recuerda (I) Dos ángulos son complementarios si suman un ángulo recto, es decir, 90º. Dos ángulos son suplementarios si suman dos ángulos rectos, es decir, 180º.

3. Recuerda: igualdad de ángulos Son iguales: Los ángulos de lados paralelos Los ángulos opuestos por el vértice Los ángulos de lados perpendiculares En todos estos casos

4. Suma de los ángulos interiores de un triángulo La suma de los ángulos interiores de un triángulo es 180º. Sea traza por A una paralela a la base.

5. Suma de los ángulos interiores de un polígono La suma S de los ángulos interiores de un polígono vale S = 180º . (n – 2) Si n es el número de lados, el n ú mero de triángulos que se forman al trazar las diagonales es n – 2, por lo que tendremos: Triángulos 6 – 2 = 4 5 – 2 = 3 4 – 2 = 2 Dibujo Polígono Cuadril á tero Pentágono Exágono Suma de los ángulos 2 . 180º = 360 3 . 180º = 360º 4 . 180º = 720º Lados 6 5 4

6. Recuerda (II) Dos ángulos son opuestos por el vértice si tienen el mismo vértice y los lados de uno de ellos son prolongación de los lados del otro. Dos ángulos opuestos por el vértice son iguales. Mediatriz de un segmeno es la recta perpendicular al segmento en su punto medio. Todos los puntos de la mediatriz equidistan de los extremos del segmento

7. Recuerda (III) Bisectriz de un ángulo es la semirecta que parte del vértice del ángulo y lo divide en dos ángulos i g uales. Todos los puntos de la bise c triz equidistan de cada lado del ángulo. Teorema de Tales. Toda paralela a un lado de un triángulo, que corta a los otros dos lados, forma un triá n gulo semejante al primero.

8. Mediatrices y circuncentro Mediatrices de un triángulo son la mediatrices de sus lados. La mediatriz m 1 está formada por los puntos que equidistan de A y B. La mediatriz m 2 está formada por los puntos que equidistan de B y C. La mediatriz m 3 está formada por los puntos que equidistan de A y C. Luego el punto O pertenece a las tres mediatrices y equidista de A, B y C El punto donde se encuentran las tres mediatrices se llama circuncentro . Es el centro de la circunferencia circunscrita que pasa por los tres vértices. m 1 m 2 m 3

9. Bisectrices e incentro Bisectrices de un triángulo son las bisectrices de sus ángulos. La bisectriz b 1 está formada por los puntos que equidistan de los lados AB yAC. La bisectriz b 2 está formada por los puntos que equidistan de los lados AB y AC. La bisectriz b 3 está formada por los puntos que equidistan de los lados CB y CA. Luego el punto I pertenece a las tres bisectrices y equidista de los tres lados del triángulo. El punto donde se encuentran las tres bisectrices se llama incentro . Es el centro de la circunferencia inscrita, tangente a los tres lados. b 1 b 2 b 3

10. Medianas y baricentro Medianas de un triángulo son las rectas que pasan por un vértice y el punto medio del lado opuesto. Las medianas de un triángulo se cortan en un punto B. El punto donde se encuentran las tres medianas se llama baricentro . Cada mediana divide al triángulo en dos de igual área. El baricentro dista el d o ble del vértice que del punto medio del lado. Para conseguir colocar un triángulo en equilibrio sobre la punta de un lápiz habría que colocarlo en el punto B.

11. Alturas y ortocentro Alturas de un triángulo son las rectas perpendiculares a los lados que pasan por los vértices opuestos. El punto donde se encuentran las tres alturas se llama ortocentro. A, B y C son los puntos medios de los lados del triángulo A'B'C'. Por tanto las alturas de ABC son mediatrices de A'B'C’. Por tanto se cortan en el punto O, que será el circuncentro de A'B'C'.

12. Figuras semejantes Dos figuras que tienen la misma forma, aun con diferentes dimensiones, se llaman semejantes. Dos figuras son semejantes si sus ángulos correspondientes son iguales y sus lados correspondientes proporcionales. Los elementos que se corresponden (puntos, segmentos, ángulos …) se llaman homólogos.

13. Semejanza de figuras en el plano Dos figuras del plano son semejantes si los cocientes de de los segmentos determinados por pares cualesquiera de puntos correspondientes son iguales. es la razón de semejanza

14. La semejanza en el plano Los siguientes cuadrados son semejantes a escala 2 y 3. Si el lado del primer cuadrado vale 3 cm, los lados de los otros son 6 y 9 cm. Los perímetros respectivos serán: 12 cm, 24 cm y 36 cm. Han quedado multiplicados por 2 y por 3, respectivamente, que es la razón de semejanza. Si dos figuras son semejantes con razón de semejanza k, la razón de sus perímetros es k. 200 % 300 % 3 cm 6 cm 9 cm p = 4 · 3 = 12 cm p = 4 · 3 · 2 = 24 cm p = 4 · 3 · 3 = 36 cm

15. La semejanza en el plano Los siguientes cuadrados son semejantes a escala 2 y 3, respectivamente.. Si el lado del primer cuadrado vale 3 cm, los lados de los otros son 6 y 9 cm. Las áreas respectivas serán: 9 cm 2 , 36 cm 2 y 81 cm 2 . Han quedado multiplicados por 2 2 y por 3 2 , respectivamente; por el cuadrado de la razón de semejanza respectiva. Si dos figuras son semejantes con razón de semejanza k, la razón de sus áreas es k 2 . S´ = S · k 2 200 % 300 % 3 cm 6 cm 9 cm S = 3 · 3 = 9 cm 2 S´ = (3 · 2) 2 = 9 · 2 2 = 36 cm 2 S´´ = (3 · 3) 2 = 9 · 3 2 = 81 cm 2

16. Triángulos semejantes Dos triángulos son semejantes si tienen: los lados proporcionales y los ángulos iguales La semejanza de triángulos se simboliza: El cociente se llama razón de semejanza

17. Criterios de semejanza de triángulos (I) Por aplicación del Teorema de Tales se demuestra que A'B"C" es semejante a A'B'C' y por tanto ABC y A'B'C' también lo son Dos triángulos son semejantes si tienen dos ángulos iguales Se construye A'B"C" sobre A'B'C’. Para ello: Se toma A'B" = AB Por B" se traza una paralela al lado B'C' Se puede demostrar ahora que ABC = A'B"C" Partimos de dos triángulos ABC y A'B'C' que tienen dos ángulos iguales y por lo tanto los tres.

18. Criterios de semejanza de triángulos (II) Por aplicación del Teorema de Tales se demuestra que A'B"C" es semejante a A'B'C' y por tanto ABC y A'B'C' también lo son Dos triángulos son semejantes si tienen los tres lados proporcionales Se construye A'B"C" sobre A'B'C’. Para ello: Se toma A'B" = AB Por B" se traza una paralela a lado B'C' Se puede demostrar ahora que ABC = A'B"C" Partimos de dos triángulos ABC y A'B'C' que tienen los lados proporcionales.

19. Criterios de semejanza de triángulos (III) Por aplicación del Teorema de Tales se demuestra que A'B"C" es semejante a A'B'C' y por tanto ABC y A'B'C' también lo son Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido igual. Se construye A'B"C" sobre A'B'C’. Para ello: Se toma A'B" = AB Por B" se traza una paralela a lado B'C' Se puede demostrar ahora que ABC = A'B"C" Partimos de dos triángulos ABC y A'B'C' que tienen dos lados propocionales y los ángulos A y A' iguales

20. Teorema de Tales Toda recta paralela a un lado de un triángulo, que corta a los otros dos lados, determina un triángulo semejante al grande. Los triángulos ABC y AB'C' son semejantes Triángulos semejantes, aunque en el segundo caso de orientación diferente.

21. Teorema de Tales b) Los ángulos son iguales: Construimos un triángulo ABC de lados 12 cm, 15 cm y 18 cm. C´ a) Si medimos los valores de los lados de cada uno de los triángulos se observa que son proporcionales: 4 Los triángulos AB´C´ y ABC son semejantes: Este resultado es válido para cualquier recta paralela a un lado y su enunciado constituye el teorema de Tales. Toda paralela a un lado de un triángulo, que corta a los otros dos lados, determina un triángulo semejante al grande. 12 18 15 B C A por tener los lados paralelos. B´ Sobre el lado AB elegimos un puntos B´de forma que AB´= 4 cm. Trazamos una paralela al lado BC por B´. Esta recta cortará al lado AC en C´.

22. Teorema de Pitágoras En un triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Si los lados de un triángulo verifican la relación de Pitágoras, el triángulo es rectángulo. 3 2 + 4 2 = 5 2