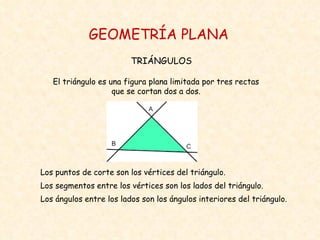
Este documento describe las características básicas de los triángulos en geometría plana. Explica que un triángulo está delimitado por tres segmentos que se cortan dos a dos y clasifica los triángulos según sus ángulos y lados. También describe puntos, segmentos y rectas notables como las medianas, alturas, bisectrices y mediatrices de cualquier triángulo, incluyendo el baricentro, ortocentro e incentro.

1. GEOMETRÍA PLANA EMAIL: [email_address] Juan Carlos Muñoz Villarroel TRIÁNGULOS

2. GEOMETRÍA Las pirámides de Egipto

3. GEOMETRÍA Figuras geométricas en Inglaterra de origen misterioso

4. GEOMETRÍA Estructuras

5. GEOMETRÍA PLANA TRIÁNGULOS El triángulo es una figura plana limitada por tres rectas que se cortan dos a dos. Los puntos de corte son los vértices del triángulo. Los segmentos entre los vértices son los lados del triángulo. Los ángulos entre los lados son los ángulos interiores del triángulo.

6. GEOMETRÍA PLANA CLASIFICACIÓN DE TRIÁNGULOS: A) Por sus ángulos: B) Por sus lados: Un ángulo igual a 90º. Un ángulo mayor que 90º. Los tres ángulos menores que 90º. Los tres lados iguales. Dos lados iguales. Los tres lados desiguales.

7. GEOMETRÍA PLANA PUNTOS, SEGMENTOS Y RECTAS NOTABLES DE UN TRIÁNGULO. Sea un triángulo cualquiera ABC y los puntos medios de cada lado D, E y F. Trazamos las medianas CD, BE y AF. El punto de intersección de las medianas es el Baricentro o centro de gravedad. El baricentro está a 2/3 desde cada vértice y el punto medio de su lado opuesto. 1. MEDIANAS.

8. GEOMETRÍA PLANA PUNTOS, SEGMENTOS Y RECTAS NOTABLES DE UN TRIÁNGULO. 2. ALTURAS. Sea un triángulo cualquiera ABC. Trazamos las alturas desde cada vértice hacia el lado opuesto. El punto de intersección de las alturas es el Ortocentro . Nota: En los triángulos obtusángulos, el ortocentro se halla en el exterior del mismo.

9. GEOMETRÍA PLANA PUNTOS, SEGMENTOS Y RECTAS NOTABLES DE UN TRIÁNGULO. 3. BISECTRICES. Sea un triángulo ABC. Trazamos las bisectrices de cada ángulo interior. La intersección de las tres bisectrices es el Incentro y es el centro de la circunferencia inscrita. (tangente a los tres lados del triángulo).

10. GEOMETRÍA PLANA PUNTOS, SEGMENTOS Y RECTAS NOTABLES DE UN TRIÁNGULO. 4. MEDIATRICES. Sea un triángulo ABC. Trazamos las mediatrices de cada lado. La intersección de las tres mediatrices es el Circuncentro y es el centro de la circunferencia circunscrita. (pasa por los tres vértices).

11. GEOMETRÍA PLANA PUNTOS, SEGMENTOS y RECTAS NOTABLES DE UN TRIÁNGULO. Sea un triángulo ABC. Medianas. Alturas. Bisectrices. Mediatrices. Para cualquier triángulo, existe una recta que pasa siempre por tres puntos notables. Es la recta de EULER.