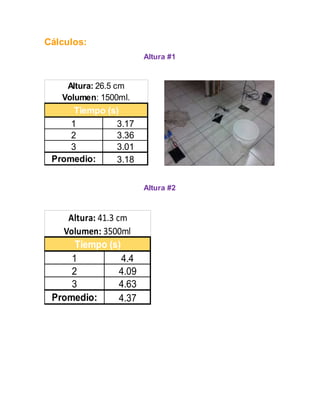
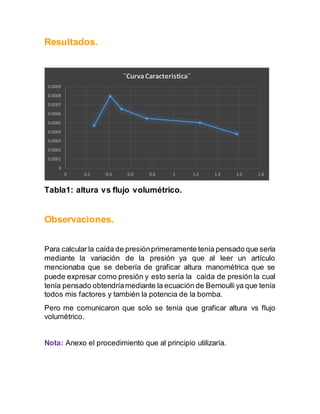
Este documento describe un experimento para medir el flujo volumétrico de una bomba a diferentes alturas. Se midió el tiempo que tomó llenar un volumen fijo de agua para varias alturas de la manguera conectada a la bomba. Luego, se calculó el flujo volumétrico en cada caso usando la ecuación de continuidad. Finalmente, se graficó la altura contra el flujo volumétrico para obtener la curva característica de la bomba.

1. Instituto Tecnológico
De Mexicali
Ing. Química
Laboratorio Integral I
Practica #3
Ramírez Miriam.
Curvas características.

2. Objetivo.
Es el poder observar cómo afecta la altura ala potencia al igual que la
fricción en el fluido.
Introducción.
La curva característica de una bomba describe la relación entre la altura
manométrica (caída de presión) y el caudal, datos que permiten escoger
la bomba más adecuada para cada instalación. La altura manométrica
de una bomba es una magnitud, expresable también como presión, que
permite valorar la energía suministrada al fluido, es decir, se trata de la
caída de presión que debe de vencer la bomba para que el fluido circule
según condiciones de diseño.
Marco Teórico.
Factor de fricción:
La fórmula de Darcy puede ser deducida por el análisis dimensional con
la excepción del factor de fricción f, que debe ser determinado
experimentalmente. El factor de ficción para condiciones de flujo laminar
es de (Re<2000) es función sola del número de Reynolds, mientras que
para flujo turbulento (Re>4000) es también función del tipo de pared de
tubería.
Curva característica:

3. Las curvas características de las bombas, representan el comportami
ento de los parámetros de las bombas para el rango de caudales que
estas manejen.
Material.
 3 soportes universales
 3 pinzas
 Vaso de prese pitado de 3,500 ml.
 Cubeta
 Cronometro
 Manguera
 Agua
 Bomba
Procedimiento.
1.- Se coloca la manguera a la misma altura de la bomba.
2.- Con ayuda de los soportes universales mantienes la manguera
rígida.
3.- Vierte en la cubeta lo suficiente para cubrir la altura de la bomba.
4.- Coloca el vaso al final de la manguera.
5.- Una vez que el equipo esté listo se acciona la bomba y se toma el
tiempo de llenado a un cierto volumen.
6.-una vez tomado el tiempo y que este sea el correcto seba a
aumentando la altura de la manguera.

4. Cálculos:
Altura #1
Altura #2
Altura: 26.5 cm
Volumen: 1500ml.
Tiempo (s)
1 3.17
2 3.36
3 3.01
Promedio: 3.18
Altura: 41.3 cm
Volumen: 3500ml
Tiempo (s)
1 4.4
2 4.09
3 4.63
Promedio: 4.37

5. Altura #3
Altura #4
Altura: 52 cm
Volumen: 3500ml
Tiempo (s)
1 5.46
2 5.29
3 5.23
Promedio: 5.33
Altura: 75 cm
Volumen: 3500ml
Tiempo (s)
1 6.38
2 6.43
3 6.28
Promedio: 6.36
Altura #5 Altura #6
Altura: 124 cm
Volumen: 3500ml
Tiempo (s)
1 6.92
2 6.86
3 7
Promedio: 6.93
Altura: 158 cm
Volumen: 3500ml
Tiempo (s)
1 9.24
2 8.82
3 9.64
Promedio: 9.23

6. Para la altura #1
Volumen= 1500ml/1000 = 1.5 lts. Convirtiendo el volumen a 풎ퟑ
ퟏ 풎ퟑ
ퟏퟎퟎퟎ 풍풕풔.
1.5lts.
= ퟏ. ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ ec. (1)
Calculo del flujo volumétrico:
푽̇
=
푽
풕
F (1)
Sustituyendo la ecuación 1 en F (1):
푽̇
ퟏ.ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ
=
ퟑ.ퟏퟖ 풔풆품.
푽̇
=4.71xퟏퟎ−ퟎퟒ 풎ퟑ
풔풆품.
Para la altura #2
Volumen= 3500ml/1000 = 3.5 lts. Convirtiendo el volumen a 풎ퟑ
ퟏ 풎ퟑ
ퟏퟎퟎퟎ 풍풕풔.
3.5lts.
= ퟑ. ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ ec. (1)
Calculo del flujo volumétrico:
푽̇
=
푽
풕
F (1)
Sustituyendo la ecuación 1 en F (1):
푽̇
ퟑ.ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ
=
ퟒ,ퟑퟕ 풔풆품.
푽̇=8xퟏퟎ−ퟎퟒ 풎ퟑ
풔풆품.

7. Para la altura #3
Volumen= 3500ml/1000 = 3.5 lts. Convirtiendo el volumen a 풎ퟑ
ퟏ 풎ퟑ
ퟏퟎퟎퟎ 풍풕풔.
3.5lts.
= ퟑ. ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ ec. (1)
Calculo del flujo volumétrico:
푽̇
=
푽
풕
F (1)
Sustituyendo la ecuación 1 en F (1):
푽̇
ퟑ.ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ
=
ퟓ.ퟑퟑ 풔풆품.
푽̇
=6.56xퟏퟎ−ퟎퟒ 풎ퟑ
풔풆품.
Para la altura #4
Volumen= 3500ml/1000 = 3.5 lts. Convirtiendo el volumen a 풎ퟑ
ퟏ 풎ퟑ
ퟏퟎퟎퟎ 풍풕풔.
3.5lts.
= ퟑ. ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ ec. (1)
Calculo del flujo volumétrico:
푽̇
=
푽
풕
F (1)
Sustituyendo la ecuación 1 en F (1):
푽̇
ퟑ.ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ
=
ퟔ.ퟑퟔ 풔풆품.
푽̇=5.5xퟏퟎ−ퟎퟒ 풎ퟑ
풔풆품.

8. Para la altura #5
Volumen= 3500ml/1000 = 3.5 lts. Convirtiendo el volumen a 풎ퟑ
ퟏ 풎ퟑ
ퟏퟎퟎퟎ 풍풕풔.
3.5lts.
= ퟑ. ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ ec. (1)
Calculo del flujo volumétrico:
푽̇
=
푽
풕
F (1)
Sustituyendo la ecuación 1 en F (1):
푽̇
ퟑ.ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ
=
ퟔ.ퟗퟑ 풔풆품.
푽̇
=5.05xퟏퟎ−ퟎퟒ 풎ퟑ
풔풆품.
Para la altura #6
Volumen= 3500ml/1000 = 3.5 lts. Convirtiendo el volumen a 풎ퟑ
ퟏ 풎ퟑ
ퟏퟎퟎퟎ 풍풕풔.
3.5lts.
= ퟑ. ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ ec. (1)
Calculo del flujo volumétrico:
푽̇
=
푽
풕
F (1)
Sustituyendo la ecuación 1 en F (1):
푽̇
ퟑ.ퟓ풙ퟏퟎ−ퟎퟑ풎ퟑ
=
ퟗ.ퟐퟑ 풔풆품.
푽̇
=3.79xퟏퟎ−ퟎퟒ 풎ퟑ
풔풆품.

9. Resultados.
0.0009
0.0008
0.0007
0.0006
0.0005
0.0004
0.0003
0.0002
0.0001
0
¨Curva Caracteristica¨
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8
Tabla1: altura vs flujo volumétrico.
Observaciones.
Para calcular la caída de presión primeramente tenía pensado que sería
mediante la variación de la presión ya que al leer un artículo
mencionaba que se debería de graficar altura manométrica que se
puede expresar como presión y esto sería la caída de presión la cual
tenía pensado obtendría mediante la ecuación de Bernoulli ya que tenía
todos mis factores y también la potencia de la bomba.
Pero me comunicaron que solo se tenía que graficar altura vs flujo
volumétrico.
Nota: Anexo el procedimiento que al principio utilizaría.

10. Conclusión.
Es importante siempre calcular la potencia de la bomba debido a que
con esto se puede determinar la eficiencia como así como si hay
cavitación o no industrialmente siempre se realizan este tipo de
pruebas.
Anexos:

11. Referencias.
 Mecánica de Fluidos. Sexta edición
Mott, Robert l.
 Institute, ASHRAE Liaoning. Fundamentals of Water System
Design, SI Versión. Atlanta: s.n., 1999.