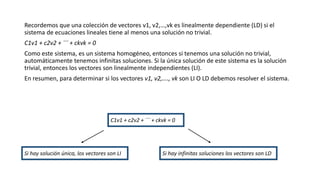
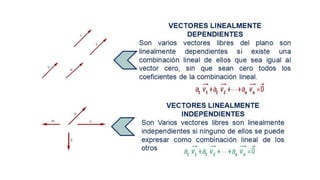
Este documento describe la dependencia e independencia lineal de vectores. Explica que un conjunto de vectores es linealmente dependiente si existe una combinación lineal no trivial de los vectores que es igual a cero, y de lo contrario es linealmente independiente. Presenta dos teoremas para determinar si un conjunto de vectores es dependiente o independiente calculando el determinante o rango de la matriz formada por los vectores.

1. EXPOSICIÓN
DEPENDENCIA E INDEPENDENCIA LINEAL
CESUN UNIVERSIDAD
CARRERA: INGENIERÍA INDUSTRIAL
DOCENTE: YASMANY JESÚS MARTÍNEZ REYES
10 DE ABRIL DE 2021
MATERIA Y UNIDAD DE LA TAREA:
ALGEBRA LINEAL
UNIDAD 3
INTEGRANTES:
DALIA ISELA SÁNCHEZ DÍAZ
ELMER EDUARDO DE LEÓN CALMO
MAXIMILIANO GUTIÉRREZ MATÍAS

2. ¿qué es dependencia e independencia lineal?
Dependencia lineal e independencia lineal
Se dice que el conjunto de vectores {v1, v2, . . . , vn} es linealmente dependiente
(LD) si existen n números ´ c1, c2, . . . , cn, no todos nulos, tales que:
c1v1 + c2v2 + · · · + cnvn = 0
Si el conjunto de vectores {v1, v2, . . . , vn} no es linealmente dependiente se dice
que es linealmente independiente (LI).

3. Recordemos que una colección de vectores v1, v2,…,vk es linealmente dependiente (LD) si el
sistema de ecuaciones lineales tiene al menos una solución no trivial.
C1v1 + c2v2 + ¨¨ + ckvk = 0
Como este sistema, es un sistema homogéneo, entonces si tenemos una solución no trivial,
automáticamente tenemos infinitas soluciones. Si la única solución de este sistema es la solución
trivial, entonces los vectores son linealmente independientes (LI).
En resumen, para determinar si los vectores v1, v2,…., vk son LI O LD debemos resolver el sistema.
C1v1 + c2v2 + ¨¨ + ckvk = 0
Si hay infinitas soluciones los vectores son LD
Si hay solución única, los vectores son LI

5. Determinar si el conjunto de vector dado es LI O
LD. Por el método de definición

8. Como comprobar si es linealmente independiente
o linealmente dependiente
Teorema 1
Si con los vectores v1, v2, . . . , vn se forman las columnas de una matriz
cuadrada A, y se calcula det(A), entonces
• 1 si det(A) ≠0 los vectores son LI
• 2 si det(A) = 0 los vectores son LD.
Ejemplo:

10. Teorema 2
Si con los vectores v1, v2, . . . , vn se forman las columnas de una matriz
A, y se calcula rango(A), entonces
• 1 si rango(A) = n los vectores son LI
• 2 si rango(A) < n los vectores son LD.
Ejemplo.

12. Conclusión
Como conclusión del trabajo podemos decir que podemos aplicar
diversos teoremas como comprobación de un conjunto de vectores si
es, LD o LI, ya que a todo esto nos dará el mismo resultado. Y podemos
deducir si un vector dado depende de otro vector o si ese vector es
linealmente independiente.

13. Fuentes consultadas
• file:///C:/Users/gutie/Downloads/Tema_Espacios%20vectoriales%20(
1).pdf
• https://www.youtube.com/watch?v=cvtCy3pbT-A
• https://www.youtube.com/watch?v=v_8cxaXIU7s&t=106s
• https://www.youtube.com/watch?v=smVGjdcMoYk&t=1s
• Dialnet-DependenciaEIndependenciaLineal-2875741 (1).pdf
• ma3002-dependencia-lineal.pdf