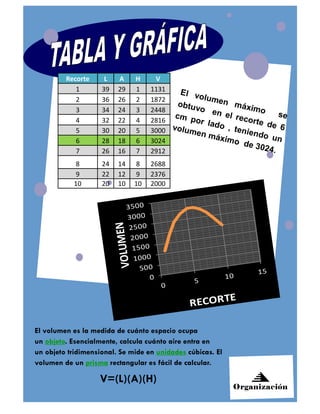
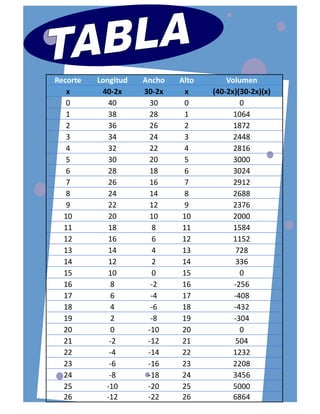
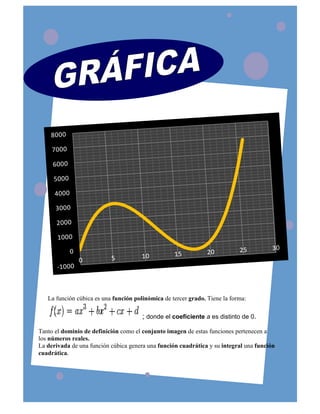
El documento describe cómo fabricar una caja sin tapa a partir de un rectángulo de cartón de 40x30 cm recortando cuadrados en cada esquina. Al recortar cuadrados de 6 cm de lado, se obtiene una caja de dimensión máxima 32x24x6 cm, con un volumen máximo de 3,024 cm3.

1. Se dispone de una pieza rectangular de cartón que mide 40x30 cm, con
este material se va a fabricar una caja sin tapa, para ellos se recortarán
cuatro cuadrados uno en cada esquina y se doblará la pieza resultante.
•
¿Cuánto deben medir los cuatro cuadrados que se recortarán par
•
que el volumen de la caja resultante sea el máximo posible?
•
¿Cuáles serán las dimensiones de la caja : largo, ancho y alto?
•
¿Cuánto es el volumen máximo?
IRMA LAURA GARCIA FAVELA
1A
PROCESOS INDUSTRIALES
Un rectángulo es un paralelogramo cuyos cuatro lados forman
ángulos rectos entre sí. Los lados opuestos tienen la misma longitud.
El perímetro de un rectángulo es igual a la suma de todos sus lados. El
área de un rectángulo es igual al producto de dos de sus lados
contiguos.
Organización

2. Recorte
1
2
3
4
5
6
7
L
39
36
34
32
30
28
26
A
29
26
24
22
20
18
16
H
1
2
3
4
5
6
7
V
1131
El v
o lu m
1872
en m
obtuv
áximo
o en
2448
se
el r ec
cm p
orte
2816
or la
de 6
do ,
t e n ie
3000 volumen
ndo
máxim
un
3024
o de
3 024 .
2912
8
9
10
24
22
20
14
12
10
8
9
10
2688
2376
2000
VOLUMEN
3500
3000
2500
2000
1500
1000
500
0
0
5
10
15
E
RECORT
El volumen es la medida de cuánto espacio ocupa
un objeto. Esencialmente, calcula cuánto aire entra en
un objeto tridimensional. Se mide en unidades cúbicas. El
volumen de un prisma rectangular es fácil de calcular.
V=(L)(A)(H)
Organización

3. Recorte
x
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Longitud
40-2x
40
38
36
34
32
30
28
26
24
22
20
18
16
14
12
10
8
6
4
2
0
-2
-4
-6
-8
-10
-12
Ancho
30-2x
30
28
26
24
22
20
18
16
14
12
10
8
6
4
2
0
-2
-4
-6
-8
-10
-12
-14
-16
-18
-20
-22
Alto
x
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
Volumen
(40-2x)(30-2x)(x)
0
1064
1872
2448
2816
3000
3024
2912
2688
2376
2000
1584
1152
728
336
0
-256
-408
-432
-304
0
504
1232
2208
3456
5000
6864

4. 80 00
70 00
60 00
50 00
40 00
30 00
20 00
10 00
0
0
5
10
15
20
25
30
-1 00 0
La función cúbica es una función polinómica de tercer grado. Tiene la forma:
; donde el coeficiente a es distinto de 0.
Tanto el dominio de definición como el conjunto imagen de estas funciones pertenecen a
los números reales.
La derivada de una función cúbica genera una función cuadrática y su integral una función
cuadrática.

5. FUNCIÓN
CÚBICA
1.
FUNCIÓN DERIVDA
Se sustituyen los valores y el resultado es el siguiente:
x1 = + 17,67591879
x2 = + 5,65741454