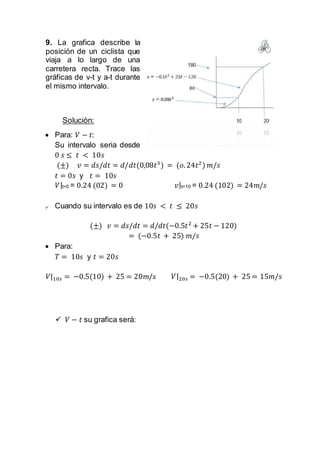
El documento describe gráficas de velocidad-tiempo (v-t) y aceleración-tiempo (a-t) para un ciclista que viaja a lo largo de una carretera recta durante 20 segundos. La gráfica de v-t muestra que la velocidad del ciclista aumenta de 0 a 24 m/s en los primeros 10 segundos y luego disminuye de 24 a 15 m/s en los siguientes 10 segundos. La gráfica de a-t muestra que la aceleración del ciclista es de 0.48 m/s2 en los primeros

1. 9. La grafica describe la
posición de un ciclista que
viaja a lo largo de una
carretera recta. Trace las
gráficas de v-t y a-t durante
el mismo intervalo.
Solución:
 Para: 𝑉 − 𝑡:
Su intervalo seria desde
0 𝑠 ≤ 𝑡 < 10𝑠
(±) 𝑣 = 𝑑𝑠/𝑑𝑡 = 𝑑/𝑑𝑡(0,08𝑡3
) = (𝑜. 24𝑡2
) 𝑚/𝑠
𝑡 = 0𝑠 y 𝑡 = 10𝑠
𝑉|t=0 = 0.24 (02) = 0 𝑣|t=10 = 0.24 (102) = 24𝑚/𝑠
 Cuando su intervalo es de 10𝑠 < 𝑡 ≤ 20𝑠
(±) 𝑣 = 𝑑𝑠/𝑑𝑡 = 𝑑/𝑑𝑡(−0.5𝑡2
+ 25𝑡 − 120)
= (−0.5𝑡 + 25) 𝑚/𝑠
 Para:
𝑇 = 10𝑠 y 𝑡 = 20𝑠
𝑉|10𝑠 = −0.5(10) + 25 = 20𝑚/𝑠 𝑉|20𝑠 = −0.5(20) + 25 = 15𝑚/𝑠
 𝑉 − 𝑡 su grafica será:

2. Para: (𝑎 − 𝑡) su
intervalo 0 ≤
𝑡 < 10𝑠
(±) 𝑎 = 𝑑𝑣/𝑑𝑡 + 𝑑/𝑑𝑡(0.24𝑡2
) = (0.48𝑡) 𝑚/𝑠
𝑡 = 0𝑠 y 𝑡 = 10𝑠
𝑎| 𝑡=0𝑠 = 0.48(10) = 0 𝑎| 𝑡=10𝑠 = 0.48(10) = (4.8) 𝑚/𝑠
 Cuando su intervalo es de: 10𝑠 < 𝑡 ≤ 20𝑠
(±) 𝑎 = 𝑑𝑣/𝑑𝑡 = 𝑑/𝑑𝑡(−0.5𝑡 + 25) = − (0.5) 𝑚/𝑠2
 a-t su grafica será:

3. 𝑉(𝑚/𝑠)
100
34
𝑣2
= 9𝑠 𝑉 = 0.25𝑠
15. La lancha navega a lo largo de una línea recta con una velocidad
descritaporla gráfica.Construya las gráficas 𝑠 − 𝑡 y 𝑎 − 𝑠. Así mismo
determine el tiempo requerido para que la lancha recorra una
distancia 𝑠 = 900𝑚 si 𝑠 = 0 cuando 𝑡 = 0.
Solución:
La gráfica “𝑠 − 𝑡”
seria desde: 0 ≤ 𝑆 < 169𝑚, 𝑠 = 0𝑚 y 𝑡 = 0𝑠.
𝑑𝑡 =
𝑑𝑠
𝑣
∫ 𝑑𝑡
𝑡
0
= ∫
𝑑𝑠
(9𝑠)
1
2
𝑠
0
𝑡 =
2√ 𝑠
3
Damos un valor ha 𝑠 = 169𝑚
𝑡 =
2√ 𝑠
3
=
2√169
3
= 8.67𝑠
La gráfica para 169 ≤ 𝑠 < 900, cuando 𝑠 = 169𝑚 y 𝑡 = 8.67𝑠.
𝑑𝑡 =
𝑑𝑠
𝑣
∫ 𝑑𝑡
𝑡
8.67
= ∫
𝑑𝑠
0.25𝑠
𝑠
169
𝑡 − 8.67 = ∫
𝑑𝑠
0.25𝑠
𝑠
169
𝑡 − 8.67 = 4[ln𝑠 − ln 169]
169 900 𝑆(𝑚)

4. 900
169
11.59𝑒 𝑡/4
= 𝑠𝑡 =
2√ 𝑠
3
𝑡
4
− 2.168 = ln(
𝑠
169
)
𝑒
𝑡
4
−2.68
=
𝑠
169
169𝑒 𝑡/4
𝑒2.68
= 𝑠
11.59𝑒 𝑡/4
= 𝑠
Cuando 𝑠 = 900𝑚
11.59𝑒 𝑡/4
= 900
𝑒 𝑡/4
= 77.65
𝑙𝑛(𝑒
𝑡
4) = 𝑙𝑛(77.65)
𝑡
4
= 4.35
𝑡 =17.40s
Hallando la gráfica de “𝑎 − 𝑠”; de 0𝑚 ≤ 𝑠 < 169𝑚,
𝑎 = 𝑣
𝑑𝑣
𝑑𝑠
= 3(𝑠1/2
)(
3
2
𝑠−1/2
)
𝑎 = 4.5𝑚/𝑠2
De 169𝑚 ≤ 𝑠 < 900𝑚,
𝑎 = 𝑣
𝑑𝑣
𝑑𝑠
= (0.25𝑠)(0.25) = 0.0625𝑠
8.67 17.4
0
𝑡(𝑠)
𝑆(𝑚)

5. 𝑎 = 4.5
𝑎 = 0.625𝑠
𝑠(𝑚)
𝑎(𝑚/𝑠2
)
10.56
56.25
169 900
Cuando 𝑠 = 169𝑚 y 𝑠 = 900𝑚,
𝑎| 𝑠=169𝑚 = 0.0625(169) = 10.56𝑚/𝑠2
𝑎| 𝑠=900𝑚 = 0.0625(900) = 56.25𝑚/𝑠2

6. 4𝑝𝑖𝑒𝑠/𝑠
36. El cable localizado en B es jalado hacia abajo a 4𝑝𝑖𝑒𝑠/𝑠 y está
desacelerando a 2𝑝𝑖𝑒𝑠/𝑠2
. Determine la velocidad y aceleración del
bloque A en este instante.
Solución:
A
4𝑝𝑖𝑒𝑠/𝑠 B
C
D
h
2𝑆𝐴
𝑆 𝐶
𝑆 𝐵
A
D
B
C

7. En el sistema se observan dos cuerdas o longitudes:
2𝑆𝐴 + (ℎ − 𝑆𝑐) = 𝑙
Derivando el espacio me da la velocidad, como 𝑙 se mantiene
contante junto con ℎ su derivada es cero:
2𝑉𝐴 − 𝑉𝐶 = 0
2𝑉𝐴 = 𝑉𝐶 ……(I)
Para la longitud siguiente aplicamos lo mismo:
Entonces: 𝑆 𝐶 + ( 𝑆 𝐶 − 𝑆 𝐵) = 𝑙
Derivando:
𝑉𝐶 + ( 𝑉𝐶 − 𝑉𝐵 ) = 0
2𝑉𝐶 = 𝑉𝐵 ……(II)
Igualando 𝑉𝐶
4𝑉𝐴 = 𝑉𝐵
Entonces:
4𝑎 𝐴 = 𝑎 𝐵
Hallando la velocidad,reemplazamos datos:
4𝑉𝐴 = −4
𝑉𝐴 = −1 = 1𝑝𝑖𝑒𝑠/𝑠 ↑
Hallando la aceleración, reemplazamos datos:
4𝑎 𝐴 = 𝑎 𝐵
4𝑎 𝐴 = 2
𝑎 𝐴 = 0.5𝑝𝑖𝑒𝑠/𝑠 ↓
39. un hombre camina a 4km/h en
la direcciónde un viento de 23km/h.
si las gotas de lluvia caen
verticalmente a 6km/h en aire
tranquilo, determine la dirección
en el cual las gotas parecen caer
con respecto al hombre. Suponga
que la rapidez horizontal de las
gotas de lluvia es igual a la del
viento.
Solución:
La velocidad de la lluvia es igual a la velocidad del viento más la
velocidad de la lluvia respectoal viento:
𝑉𝑣 = 23𝑘𝑚/ℎ
𝑉ℎ = 4𝑘𝑚/ℎ
𝜃

8. Velocidad delviento: 𝑉𝑣
⃗⃗⃗
Velocidad de la lluvia: 𝑉𝑙𝑙
⃗⃗⃗⃗
Velocidad de la lluvia
respecto al viento: 𝑉𝑙𝑙/𝑣
⃗⃗⃗⃗⃗⃗⃗⃗
“En aire tranquilo”
Velocidad delhombre: 𝑉ℎ
⃗⃗⃗⃗
Velocidad de la lluvia: 𝑉𝑙𝑙
⃗⃗⃗⃗
Velocidad de la lluvia
respecto al hombre: 𝑉𝑙𝑙/ℎ
⃗⃗⃗⃗⃗⃗⃗⃗
𝑉𝑙𝑙
⃗⃗⃗⃗ = 𝑉𝑣
⃗⃗⃗ + 𝑉𝑙𝑙/𝑣
⃗⃗⃗⃗⃗⃗⃗⃗ = −23𝑖 + (−6𝑗) = (−23𝑖 − 6𝑗)𝑘𝑚/ℎ...........(I)
La velocidad de la lluvia es igual a la velocidad del hombre más la
velocidad de la lluvia respecto al hombre:
𝑉𝑙𝑙
⃗⃗⃗⃗ = 𝑉ℎ
⃗⃗⃗⃗ + 𝑉𝑙𝑙/ℎ
⃗⃗⃗⃗⃗⃗⃗⃗ ……(II)
Remplazando la ecuación (I) en (II).
−23𝑖 − 6𝑗 = −4𝑖 + 𝑉𝑙𝑙/ℎ
⃗⃗⃗⃗⃗⃗⃗⃗
𝑉𝑙𝑙/ℎ
⃗⃗⃗⃗⃗⃗⃗⃗ = (−19𝑖 − 6𝑗) 𝑘𝑚/ℎ
|𝑉𝑙𝑙/ℎ
⃗⃗⃗⃗⃗⃗⃗⃗ | = √(−19)2 + (−6)2 = 19.92𝑝𝑖𝑒𝑠
Hallando la direcciónen la cual las gotas parecen caer con respecto
al hombre:
𝜃 = tan−1
(
6
19
) = 17.52°

9. 12.59. Un misil disparado
del reposo viaja a lo largo
de una pista recta durante
20 s con la aceleración
mostrada. Trace la gráfica
de v-t que describe el
movimiento y determine la
distancia recorrida en 20 𝑠.
Solución:
 Para el intervalo.𝑡 ≤
10𝑠.
𝑎= 12𝑡
𝑑𝑣= 𝑎𝑑𝑡
∫ 𝑑𝑣 =
𝑣
0
∫ (12𝑡)𝑑𝑡
𝑡
0
𝑣 = 6𝑡2
 Entonces cuando 𝑡 = 10𝑠. La velocidad será.
𝑣=6(10)2
𝑣 = 600 𝑚/𝑠
 Para el intervalo de 10𝑠 < 𝑡 ≤ 20𝑠.
𝑎= 4𝑡 + 40
𝑑𝑣= 𝑎𝑑𝑡
∫ 𝑑𝑣
𝑣
600
=∫ (4𝑡 + 40) 𝑑𝑡
𝑡
10
𝑣 − 600 = 2𝑡2
+ 40𝑡 − 600
𝑣 = 2𝑡2
+ 40𝑡
Entonces cuando 𝑡 = 20𝑠. La velocidad será.
𝑣 = 2(20)2
+ 40(20)
𝑣 = 1600 𝑚/𝑠
Encontramos la distancia cuando 𝑡 = 10𝑠.
𝑑𝑠 = 𝑣𝑑𝑡

10. ∫ 𝑑𝑠
𝑠
0
= ∫ (
10
0
6𝑡2
)𝑑𝑡
𝑠 = 6 ∫ ( 𝑡2) 𝑑𝑡
10
0
𝑠 = 6 [
𝑡3
3
]
10
0
𝑠 = 2𝑡3
𝑠 = 2(10)3
𝑠 = 2000𝑚
 Encontramos su distancia cuando 𝑡 = 20𝑠.
𝑑𝑠 = 𝑣𝑑𝑡
∫ 𝑑𝑠 = ∫ (2𝑡2
+ 40𝑡) 𝑑𝑡
20
10
𝑠
2000
𝑠 − 2000 = 2∫(𝑡2
)𝑑𝑡 + 40∫( 𝑡) 𝑑𝑡 /
20
10
𝑠 − 2000 =
2
3
𝑡3
+ 20𝑡2
/
20
10
𝑠 − 2000 =
2
3
(20)3
+ 20(20)2
− (
2
3
(10)3
+ 20(10)2
)
𝑆 − 2000 =
32000
3
𝑆 =
32000
3
+ 2000
𝑆 = 12667𝑚