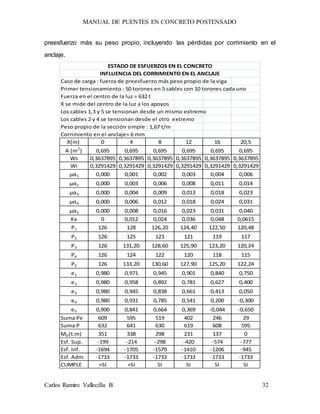
Este manual describe un puente de concreto postensado de 41 metros de longitud con 5 vanos. Presenta la planta y sección transversal del puente, describe los materiales y cargas consideradas en el diseño, y calcula la fuerza de tensionamiento requerida en dos etapas usando 50 cables en la primera etapa y 20 cables adicionales en la segunda. Finalmente, presenta las ecuaciones parabólicas que describen la trayectoria de los cables de tensionamiento a lo largo del puente.