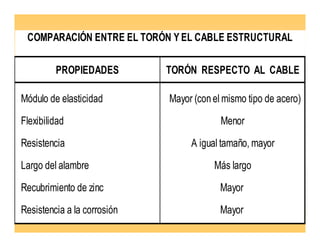
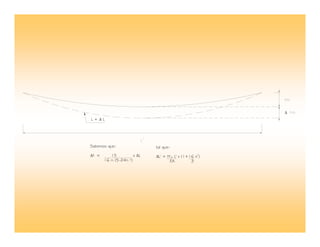
Este documento presenta aspectos estructurales relacionados al montaje de puentes colgantes. Explica la configuración típica de un puente colgante, la tecnología de cables de acero utilizados, incluyendo propiedades mecánicas y protección contra la corrosión. También describe el procedimiento constructivo, con énfasis en el análisis estático de los cables durante el lanzamiento de la superestructura del puente Nieva en Perú.

1. Ing. John Ampuero Alata
jampuero@proviasdes.gob.pe
Aspectos estructurales en elAspectos estructurales en el
montaje de puentes colgantesmontaje de puentes colgantes
III SEMINARIO DE GESTIÓN Y NORMATIVIDAD VIAL

2. INTRODUCCION
La elaboración de proyectos que involucre el empleo de
cables estructurales, sobre todo para puentes colgantes,
requiere tomar en cuenta los efectos no lineales
introducidos por los grandes desplazamientos que se
producen en este tipo de estructuras.
En este trabajo se presenta algunos aspectos a tener en
cuenta en el análisis de cables, así como de presentar una
breve descripción en lo que a tecnología de cables se
refiere.

3. TEMARIO
1.- Configuración estructural de los puentes colgantes
2.- Tecnología de cables
2.1 Definición de términos
2.2 Propiedades estructurales
2.2.1 Preestiramiento de cables
2.2.2 Módulo de elasticidad
2.3 Protección contra la corrosión
3.- Estática de cables
4.- Procedimiento constructivo
5.- Montaje de la estructura del puente colgante Nieva

4. 1.- CONFIGURACIÓN ESTRUCTURAL
TORRE
PENDOLAS
f
CABLE
PRINCIPAL
FIADOR
FIADOR
SILLASILLA
VIGA DE
RIGIDEZ
CAMARA DE
ANCLAJE
CAMARA DE
ANCLAJE
PARTES DEL PUENTE COLGANTE

5. 2.- TECNOLOGÍA DE CABLES
En aplicaciones estructurales, la palabra cable por lo
general se usa en sentido genérico para indicar un
miembro flexible solicitado a tensión. La forma o
configuración de un cable depende de su hechura;
puede componerse de barras paralelas, alambres
paralelos, cordones o torones paralelos, o torones
enrollados con trabas.

6. 2.1.- DEFINICIÓN DE TÉRMINOS
Cable. Cualquier miembro flexible a tensión que
consiste en uno o más grupos de alambres, torones,
cordeles o barras.
Alambre. Una sola longitud continua de metal
producida de una varilla mediante trefilado en frío.

7. Torón estructural (con excepción del torón de
alambres paralelos). Alambres enrollados
helicoidalmente alrededor de un alambre central
para producir una sección simétrica, producido en
los Estados Unidos de acuerdo con la norma ASTM
A586.

8. Torones de alambres paralelos. Alambres
individuales configurados en un arreglo paralelo sin
el torcimiento helicoidal.
Torones enrollados con trabas. Un arreglo de
alambres semejante al torón estructural excepto que
los alambres en algunas capas están configurados
para que queden trabados cuando se colocan
alrededor del núcleo.

10. Cable estructural. Varios torones enrollados
helicoidalmente alrededor de un núcleo formado por
un torón u otro cable, producido en los Estados
Unidos de acuerdo con la norma ASTM A603.

11. 2.2.- PROPIEDADES ESTRUCTURALES DE
LOS CABLES
Una comparación entre el esfuerzo nominal último y
admisible, a tensión, para varios tipos de cables se
presenta en la siguiente tabla:

14. Tipo Resistencia Resistencia
nominal a tensión, F pu admisible a tensión, F t
Barras ASTM A722 Tipo II 150 0.45 F pu = 67.5
(10568) (4756)
Torón enrollado con trabas 210 0.33 F pu = 70
(14795) (4882)
Torón estructural, ASTM A586 220 0.33 F pu = 73.3
(15500) (5115)
Cable estructural, ASTM A603* 220 0.33 F pu = 73.3
(15500) (5115)
Alambre paralelo 225 0.40 F pu = 90
(15852) (6341)
Alambre paralelo, ASTM A421 240 0.45 F pu = 108
(16909) (7609)
Torón paralelo ASTM A416 270 0.45 F pu = 121.5
(19023) (8560)
RESISTENCIAS NOMINALES Y ADMISIBLES DE CABLES
(1)
{klb/pulg
2
(kg/cm
2
)}

15. Diámetro Torón Cable Intervalo de diámetro Módulo máximo
nominal galvanizado galvanizado nominal, en pulg. en klb/pulg2
en pulg.
1
/2 30 (2,110) 23 (1,618) torón galvanizado
3
/4 68 (4,782) 52 (3,657) y preteestirado
1 122 (8,580) 91.4 (6,428) 1
/2 a 2 9
/16 24,000 (1'690,912)
1 1
/2 276 (19,410) 208 (14,628) 2 5
/8 y más 23,000 (1'620,458)
2 490 (34,460) 372 (26,162) cable galvanizado
3 1076 (75,672) 824 (57,950) y preestirado
4 1850 (130,105) 1460 (102,677) 3
/8 a 4 20,000 (1'409,094)
(*) Los valores corresponden a cables con revestimineto de zinc de clase A sobre todos los alambres .
Las clases B o C pueden especificarse cuando se requiere protección adicional contra la corrosión.
PROPIEDADES MECÁNICAS DE LOS CABLES DE ACERO
(1)
{klb/pulg2 (kg/cm2)}
Resistencia mínima a la ruptura (*),
de tamaños seleccionados de cables
Módulo mínimo de elasticidad,
para los intervalos indicados de diámetros

16. PROPIEDADES TORÓN RESPECTO AL CABLE
Módulo de elasticidad Mayor (con el mismo tipo de acero)
Flexibilidad Menor
Resistencia A igual tamaño, mayor
Largo del alambre Más largo
Recubrimiento de zinc Mayor
Resistencia a la corrosión Mayor
COMPARACIÓN ENTRE EL TORÓN Y EL CABLE ESTRUCTURAL

17. 2.2.1 El preestiramiento de los cables
El prealargamiento remueve el alargamiento de
construcción inherente al producto cuando sale de
las máquinas de enrollado y cerramiento..
El preestiramiento también permite, bajo cargas
prescritas, la medición precisa de longitudes y la
marcación de puntos especiales en el torón o cable
dentro de tolerancias estrechas.

18. Se lleva a cabo por el fabricante al someter sobre el
torón a una carga predeterminada durante un
intervalo de tiempo suficiente para permitir el ajuste
de las partes componentes a esa carga. La carga de
preestiramiento normalmente no excede 55% de la
resistencia última nominal del torón.

19. 2.2.4 Módulo de elasticidad
Se debe prestar atención a la correcta determinación
del módulo de elasticidad del cable, el cual varía
según el tipo de manufactura.
Dicho módulo se determina de una longitud de
probeta de al menos 100 pulg y con el área metálica
bruta del torón o cable, incluyendo el recubrimiento
de zinc, si es del caso. Las lecturas de la elongación
usadas para el cálculo del módulo de elasticidad se
toman cuando el torón o cable se estira a por lo
menos 10% del esfuerzo último establecido en la
norma o a más del 90% del esfuerzo de
preestiramiento.

20. 2.3.- PROTECCIÓN CONTRA LA CORROSIÓN
Los alambres pueden ser protegidos contra la
corrosión mediante galvanización, un recubrimiento
sacrificable de zinc que impide la corrosión del
acero mientras no se rompa dicho recubrimiento.
La efectividad del recubrimiento de zinc es
proporcional a su espesor, medido en onzas por pie
cuadrado del área superficial del alambre desnudo.
El recubrimiento de zinc clase A varía de 0.40 a 1.00
oz/pie2, dependiendo del diámetro nominal del
alambre recubierto. Un recubrimiento clase B, o
clase C es, respectivamente, 2 ó 3 veces más
pesado que el recubrimiento clase A.

21. 3.- ESTÁTICA DE LOS CABLES
TEORIA DE LOS CABLES FLEXIBLES:
La Ecuación diferencial de los cables flexibles es:
d2
y = p
dx2
To
Cuando es constante la intensidad de la carga p la descripción se aproxima a la de un
puente colgante, obteniéndose la forma parabólica del cable.
y = 4f (lx – x2
) H = wl2
l2
8f
S = L + 8/3 ( f2
/ L) ΔS = wL2 ( L + 4f )
2EA 4f 3L

22. Δ
L + Δ L
Sabemos que:
Δf1 = 15 x ΔL
16 n1 (5-24n1 )2
tal que:
ΔL' = H'pp L' x (1+16 n )
EA 3
2

23. Δ
Δ
Δ ΔΔ Δ
Δ
Δ
sabemos que:
Δf2 = 15-40n +288n x ΔL'
16n1(5-24n1 )
2 4
2
tal que:
ΔL' = Hpp(L1+L2) x Sec α
ΕΑ
3

24. Donde:
Δf1 = Aumento de flecha por alargamiento de cable entre torres
ΔL = Aumento de longitud de cable entre torres
E = Módulo de elasticidad del cable
A = Area transversal de la parte metálica del cable calculado
n1 = fm / L'
n = f / L'
Hpp = Tensión horizontal verdadera por peso propio total
H'pp = Hpp / 2 a cada lado del puente
L1 = Longitud del cable fiador izquierdo
L2 = Longitud del cable fiador derecho
Δf2 = Aumento de flecha por disminución de luz entre torres
ΔL' = Aumento de longitud de cable entre torres

25. 5.- MONTAJE DE LA SUPERESTRUCTURA DEL
PUENTE NIEVA
Tipo: Estructura metálica colgante con
fiadores descargados y con viga de
rigidez metálica base a paneles tipo
Mabey Compact 200 DSR
Longitud: 155.448 m
No de vías: 1
Ancho de vía: 4.20 m
Sup. Rodadura: Tablero metálico
Subestructura: Torres metálicas articuladas,
apoyadas sobre estribos de
concreto armado y cámaras de
anclaje de concreto.
S/C diseño: HS20 (32 t)

26. Evaluación de la posición del cable durante el lanzamiento
L1 = 47.325 L2 = 47.325 L3 = 0
ω1 = 26.4327° ω2 = 26.4327° ω3 = 26.4327°
Long. Cable 52.8501 52.8501 0 52.8501
área cable = 7.920 cm²
# cables 1 w = 23.630 kgf/m
A = 7.920 cm² (peso del cable)
E =
P = 3.100 t
S = 155.69 m α = atn(5/77.845)= 0.064142rad 3.6751°
x = 77.85 m β = atn(5/77.845)= 0.064142rad 3.6751°
Δ = 5.00 m
600,000.0 kgf/cm²
L1 X S-X L2 L3
S
ω1
αβ
ω2
ω3
Tf3
2Tf1Tf
T2 T1
P

27. Iteración N° 01 Δ = 5.00 m
24.182 t 78.005 m 39.69 cm
24.182 t 78.005 m 39.69 cm
Tensiones y deformaciones en los fiadores
Tf1 = 26.949 t δf 1 = 29.97 cm
Tf2 = 26.949 t δf 2 = 29.97 cm
Tf3 = 26.949 t δf 3 = 0.00 cm
λ1 = 69.67 cm (δf 1 +δ1) S1+ λ1 = 78.702 m
λ2 = 69.67 cm (δf 2 +δf 3+δ2) S2+ λ2 = 78.702 m
Desplazamiento horizontal del punto cargado
0.000 m
luego 11.583 m
Iteración N° 02 Δ = 11.583 m
Δ = 11.583 m α1 = 0.147712rad 8.4633°
β1 = 0.147712rad 8.4633°
=
α+βα
=
sentan.cos
P
1T
=
β
α
=
cos
cos.1T
2T
=Δ+−= 22
)xS(1S ==δ
E.A
1S.1T
1
=Δ+= 22
x2S ==δ
E.A
2S.2T
2
( ) ( ) =−
λ−−λ+
+=δ x
S.2
11S22S
2
S
22
h
( ) ( ) =δ+−λ+=Δ
2
h
2
x22S

28. luego 9.196 m
Iteración N° 12 Δ = 9.196 m
Δ = 9.196 m α1 = 0.117590rad 6.7374°
β1 = 0.117590rad 6.7374°
13.212 t 78.386 m δ1 = 21.79 cm
13.212 t 78.386 m δ2 = 21.79 cm
Tf1 = 14.652 t δf 1 = 16.30 cm
Tf2 = 14.652 t δf 2 = 16.30 cm
Tf3 = 14.652 t δf 3 = 0.00 cm
λ1 = 38.09 cm (δf 1 +δ1) S1+ λ1 = 78.386 m
λ2 = 38.09 cm (δf 2 +δf3+δ2) S2+ λ2 = 78.386 m
Desplazamiento horizontal del punto cargado
0.000 m
luego 9.196 m
( ) ( ) =δ+−λ+=Δ
2
h
2
x22S
=
α+βα
=
111 sentan.cos
P
1T
=
β
α
=
1
1
cos
cos.1T
2T
( ) ( ) =−
λ−−λ+
+=δ x
S.2
11S22S
2
S
22
h
( ) ( ) =δ+−λ+=Δ
2
h
2
x22S
=Δ+−= 22'
1 )xS(S
=Δ+= 22'
2 xS

39. GRACIAS POR SU ATENCIÓN