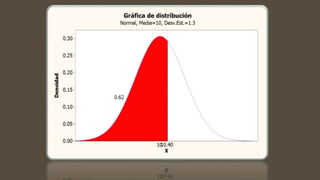
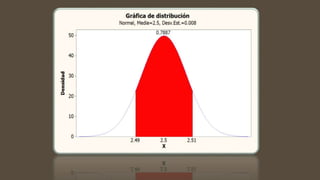
Este documento contiene varios problemas de estadística relacionados con la distribución normal. Los problemas involucran calcular puntajes z, probabilidades y percentiles asociados con variables aleatorias normales en diferentes contextos como espesor de láminas de aluminio, tiempo de vida de baterías y diámetro de cojinetes de bolas. Las soluciones a los problemas implican convertir valores a unidades estándar usando tablas z y calcular áreas bajo la curva de la distribución normal.

1. DISTRIBUCIÓN NORMAL
PROBLEMAS…
Cinthia Yamile Medina Morán
2º D
Lic. Gerardo Edgar Mata Ortiz

3. PROBLEMA 4.39
Las láminas de aluminio utilizadas para fabricar latas de bebida
tienen un espesor (en milésimas de pulgada) que se distribuye
normalmente con una media de 10 y desviación estándar de 1.3. Una
lámina particular tiene un espesor de 10.8 milésimas de pulgadas.
Determine el puntaje z.

5. PROBLEMA 4.45
Los tiempos de vida de las baterías en cierta aplicación se distribuyen
normalmente con media de 50 horas y desviación estándar de cinco
horas. Determine la probabilidad de que se elija aleatoriamente una
batería que dure entre 42 y 52 horas.
Solución:
Sea X el tiempo de vida de una batería elegida aleatoriamente.
Entonces X N. El área sombreada representa P(42 X 52), la
probabilidad de que una batería seleccionada de forma aleatoria
tenga una duración entre 42 y 52 horas. Para calcular esta área, se
hará uso de la tabla z. Primero se necesita convertir las cantidades 42
y 52 a unidades estándar. Se tiene:
De la tabla z, el área a la izquierda de z 1.60 es 0.0548, y el área a la
izquierda de z 0.40 es 0.6554. La probabilidad de que una batería
tenga tiempo de vida entre 42 y 52 horas es 0.6554 0.0548 0.6006.

7. PROBLEMA 4.46
Con referencia al ejemplo 4.45, determine el 40º percentil de los
tiempos de vida de las baterías.
De la tabla z, el área más cercana a 0.4000 es 0.4013,
correspondiente al puntaje z de 0.25. La población de los tiempos de
vida tiene una media de 50 y una desviación estándar de 5. El 40º
percentil es el punto 0.25 desviaciones estándar menor a la media.
Este valor se determina al convertir el puntaje z en uno nuevo.

9. PROBLEMA 4.47
Un proceso fabrica cojinetes de bolas cuyos diámetros se distribuye
normalmente con media de 2.505 cm y desviación estándar de 0.008
cm. Las especificaciones requieren que el diámetro esté dentro del
intervalo 2.5 0.01 cm. ¿Qué proporción de cojinetes de bolas cumple
con la especificación?
Solución

11. PROBLEMA 4.48
Con referencia al ejemplo 4.47, el proceso puede recalibrarse para
que la media sea igual a 2.5 cm, el centro del intervalo de la
especificación. La desviación estándar del proceso sigue siendo de
0.008 cm. ¿Qué proporción de los diámetros satisface la
especificación? Solución El método de solución es el mismo que en el
ejemplo 4.47. La media es de 2.500 en vez de 2.505. Los cálculos se
realizan de la siguiente manera:
El área a la izquierda de z= - 1.25 es 0.1056. El área a la izquierda
de z=1.25 es 0.8944. El área entre z=1.25 y z= -1.25 es 0.8944 -
0.1056 =0.7888. Véase la figura 4.12. El recalibrado aumenta a
78.88% la proporción de diámetros que satisface la especificación.

13. PROBLEMA 4.49
Con referencia a los ejemplos 4.47 y 4.48, suponga que se ha
recalibrado el proceso de tal forma que la media del diámetro mide
ahora 2.5 cm. ¿A qué valor debe reducirse la desviación estándar para
que 95% de los diámetros satisfaga la especificación?
Solución