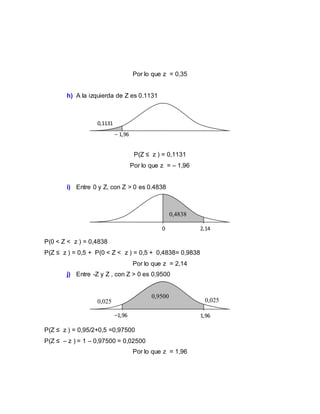
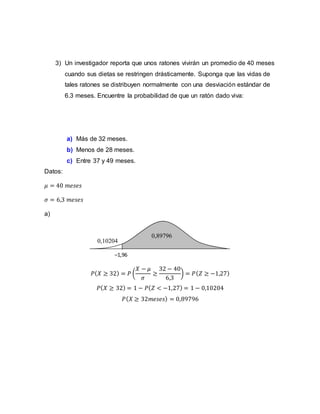
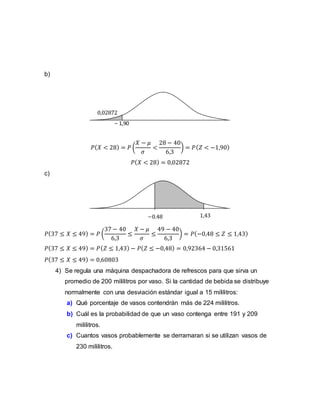
1) El documento presenta 5 ejercicios sobre distribuciones normales estándar. Resuelve áreas bajo la curva para diferentes valores de Z y encuentra valores de Z dados áreas bajo la curva. 2) Analiza la vida esperada de ratones con dietas restringidas y calcula probabilidades asociadas a diferentes rangos de meses de vida. 3) Estudia una máquina dispensadora de refrescos y calcula probabilidades de cantidades de mililitros servidos.

1. República Bolivariana De Venezuela
Ministerio Del Poder Popular Para La Educación Superior
Instituto Universitario De Tecnología
Antonio José De Sucre
Barquisimeto-Lara
EJERCICIOS 2
Integrante:
María Verónica Rojas Blanco
C.I: 22315701

2. Resuelve los siguientes ejercicios y realiza la gráfica en cada caso.
Empleando una tabla de distribución normal, acumulada a la izquierda para
resolver estos ejercicios:
1) Dada una distribución normal estándar, grafique y encuentre el área bajo
la curva que está :
a) A la izquierda de Z = 1.43
P (Z < 1,43) = 0,92364
b) A la derecha de Z = -0.89
P( Z > – 0,89 ) =1 – P (Z < – 0,89) = 1 – 0,18673 = 0,81327
c) Entre Z = -2.16 y Z = - 0,65
P(– 2,16 <Z < – 0,65 ) = P (Z ≤ – 0,65) – P (Z ≤– 2,16) = 0,25785 – 0,01539=
0,24246
1,43
0,9236
4
– 0,89
0,18673
– 2,16 – 0,65
0,81327

3. d) A la izquierda de Z = -1.39
P( Z < – 1,39 ) = 0,08226
e) A la derecha de Z =1.96
P( Z > 1,96 ) =1 – P (Z ≤ 1,96) = 1 – 0,97500 = 0,02500
f) Entre Z =-0.48 y Z = 1.74
P( – 0,48 < Z < 1,74 ) = P (Z ≤ 1,74) – P (Z ≤ – 0,48) = 0,95907 – 0,31561=
0,64346
2) Encuentre el valor de Z si el área bajo una curva normal estándar y graficar:
g) A la derecha de Z es 0.3622
P(Z ≤ z ) = 1 – P(Z > z ) = 1 – 0,3622 = 0,6378
– 1,39
0,08226
0,02500
1,96
0,97500
– 0,48 1,74
0,64346
0,35
0,36220,6378

4. Por lo que z = 0,35
h) A la izquierda de Z es 0.1131
P(Z ≤ z ) = 0,1131
Por lo que z = – 1,96
i) Entre 0 y Z, con Z > 0 es 0.4838
P(0 < Z < z ) = 0,4838
P(Z ≤ z ) = 0,5 + P(0 < Z < z ) = 0,5 + 0,4838= 0,9838
Por lo que z = 2,14
j) Entre -Z y Z , con Z > 0 es 0,9500
P(Z ≤ z ) = 0,95/2+0,5 =0,97500
P(Z ≤ – z ) = 1 – 0,97500 = 0,02500
Por lo que z = 1,96
– 1,96
0,1131
0 2,14
0,4838
–1,96 1,96
0,9500
0,025 0,025

5. 3) Un investigador reporta que unos ratones vivirán un promedio de 40 meses
cuando sus dietas se restringen drásticamente. Suponga que las vidas de
tales ratones se distribuyen normalmente con una desviación estándar de
6.3 meses. Encuentre la probabilidad de que un ratón dado viva:
a) Más de 32 meses.
b) Menos de 28 meses.
c) Entre 37 y 49 meses.
Datos:
𝜇 = 40 𝑚𝑒𝑠𝑒𝑠
𝜎 = 6,3 𝑚𝑒𝑠𝑒𝑠
a)
𝑃( 𝑋 ≥ 32) = 𝑃 (
𝑋 − 𝜇
𝜎
≥
32 − 40
6,3
) = 𝑃( 𝑍 ≥ −1,27)
𝑃( 𝑋 ≥ 32) = 1 − 𝑃( 𝑍 < −1,27) = 1 − 0,10204
𝑃( 𝑋 ≥ 32𝑚𝑒𝑠𝑒𝑠) = 0,89796
–1,96
0,89796
0,10204

6. b)
𝑃( 𝑋 < 28) = 𝑃 (
𝑋 − 𝜇
𝜎
<
28 − 40
6,3
) = 𝑃( 𝑍 < −1,90)
𝑃( 𝑋 < 28) = 0,02872
c)
𝑃(37 ≤ 𝑋 ≤ 49) = 𝑃 (
37 − 40
6,3
≤
𝑋 − 𝜇
𝜎
≤
49 − 40
6,3
) = 𝑃(−0,48 ≤ 𝑍 ≤ 1,43)
𝑃(37 ≤ 𝑋 ≤ 49) = 𝑃( 𝑍 ≤ 1,43) − 𝑃( 𝑍 ≤ −0,48) = 0,92364 − 0,31561
𝑃(37 ≤ 𝑋 ≤ 49) = 0,60803
4) Se regula una máquina despachadora de refrescos para que sirva un
promedio de 200 mililitros por vaso. Si la cantidad de bebida se distribuye
normalmente con una desviación estándar igual a 15 mililitros:
a) Qué porcentaje de vasos contendrán más de 224 mililitros.
b) Cuál es la probabilidad de que un vaso contenga entre 191 y 209
mililitros.
c) Cuantos vasos probablemente se derramaran si se utilizan vasos de
230 mililitros.
– 1,90
0,02872
−0,48 1,43

7. d) Por debajo de que valor obtendremos 25 % de las bebidas más
pequeñas.
Datos:
𝜇 = 200 𝑚𝑙
𝜎 = 15 𝑚𝑙
a)
𝑃( 𝑋 ≥ 224) = 𝑃 (
𝑋 − 𝜇
𝜎
≥
224 − 200
15
) = 𝑃( 𝑍 ≥ 1,6)
𝑃( 𝑋 ≥ 224) = 1 − 𝑃( 𝑍 < 1,6) = 1 − 0,94520
𝑃( 𝑋 ≥ 224𝑚𝑙) = 0,05480
b)
𝑃(191 ≤ 𝑋 ≤ 209) = 𝑃 (
191 − 200
15
≤
𝑋 − 𝜇
𝜎
≤
209 − 200
15
) = 𝑃(−0,6 ≤ 𝑍 ≤ 0,6)
𝑃(191 ≤ 𝑋 ≤ 209) = 𝑃( 𝑍 ≤ 0,6) − 𝑃( 𝑍 ≤ −0,6) = 0,72575 − 0,27425
𝑃(191 ≤ 𝑋 ≤ 209) = 0,45149
1,6
−0,6 0,6

8. c)
𝑃( 𝑋 ≥ 230) = 𝑃 (
𝑋 − 𝜇
𝜎
≥
230 − 200
15
) = 𝑃( 𝑍 ≥ 2)
𝑃( 𝑋 ≥ 230) = 1 − 𝑃( 𝑍 < 2) = 1 − 0,97725
𝑃( 𝑋 ≥ 230𝑚𝑙) = 0,02275
Conclusión:
Se derrama el 2,275% de los vasos.
d)
𝑧 =
𝑋 − 𝜇
𝜎
⇒ 𝜇 + 𝑧𝜎 = 𝑋 ⇒ 𝑋 = 200 − 0,67 ∙ 15 = 189,88265
Conclusión:
Por debajo de 189,9ml obtendremos 25 % de las bebidas más pequeñas.
5) Los valores de coeficiente de inteligencia (CI) en seres humanos están
distribuidos normalmente, con media igual a 100 y desviación estándar
igual a 10. Si una persona es elegida al azar, cual es la probabilidad de
que su CI esté entre 100 y 115.
2
0,25
- 0,67

9. Datos:
𝜇 = 100
𝜎 = 10
𝑃(100 ≤ 𝑋 ≤ 115) = 𝑃 (
100 − 100
10
≤
𝑋 − 𝜇
𝜎
≤
115 − 100
10
) = 𝑃(0 ≤ 𝑍 ≤ 1,5)
𝑃(100 ≤ 𝑋 ≤ 115) = 𝑃( 𝑍 ≤ 1,5) − 𝑃( 𝑍 ≤ 0) = 0,93319− 0,5
𝑃(100 ≤ 𝑋 ≤ 115) = 0,43319
Conclusión:
La probabilidad de que su CI esté entre 100 y 115 es 0,43319.
0 1,5