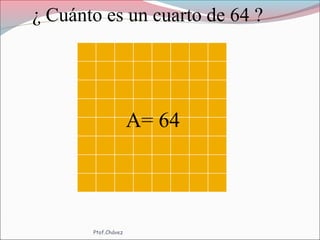
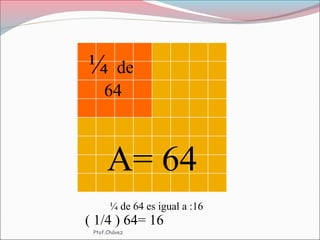
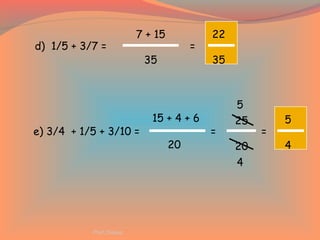
El documento presenta una metodología para la enseñanza de los números fraccionarios, que incluye definiciones, operaciones con fracciones y ejercicios prácticos. Se discuten fracciones equivalentes, orden de las fracciones y cómo realizar sumas y restas tanto de fracciones homogéneas como heterogéneas. Se incluyen ejemplos y ejercicios para facilitar el aprendizaje de los estudiantes.

1. Metodología para la
enseñanza de los
números Fraccionarios
Ptof.Chávez

2. Definición de fracciones.
Fracciones como operadores.
Fracciones equivalentes.
Orden de las fracciones.
Suma de fracciones.
Resta de fracciones.
Multiplicación de fracciones.
División de fracciones.Ptof.Chávez

3. Números Fraccionarios
Ptof.Chávez

4. Ptof.Chávez

5. Ptof.Chávez

6. 1/2
1/2
La unidad
dividida en
dos partes
iguales, le
llamamos a
cada una un
medio.
Ptof.Chávez

7. 1/4
1/41/4
1/4
La unidad dividida en cuatro partes
iguales, le llamaremos a cada una de
estas un cuarto.
Ptof.Chávez

8. ¡ Regresamos a la Unidad , bueno a la
manzana !
¿ Deseas conocer más ?
Ptof.Chávez

9. Ptof.Chávez

10. Para numerar cada una de las partes
en que se divide la unidad, utilizamos
los números Fraccionarios, que tiene
la forma
a
b
NUMERADORNUMERADOR
DENOMINADORDENOMINADOR
Donde “a” representa las partes que se han tomado de la
unidad y “b”, las partes en que se divide la unidad.
Ptof.Chávez

11. 1/4
Un cuarto, uno de cuatro partes iguales
en que se dividió la unidad.
Ptof.Chávez

12. 2/4
Dos Cuartos, dos de cuatro partes igualesDos Cuartos, dos de cuatro partes iguales
en que se dividió la unidaden que se dividió la unidad
Ptof.Chávez

13. 3/4
Tres Cuartos, tres de cuatro partes igualesTres Cuartos, tres de cuatro partes iguales
en que se dividió la unidaden que se dividió la unidad
Ptof.Chávez

14. 4/4Cuatro Cuartos, cuatro de cuatro partesCuatro Cuartos, cuatro de cuatro partes
iguales en que se dividió la unidadiguales en que se dividió la unidad
Ptof.Chávez

15. Definición deDefinición de
FracciónFracción
. . . . . . . . . . .
.......
Ptof.Chávez

16. 55
66
De la unidad dividida en seis partes,De la unidad dividida en seis partes,
se han tomado cinco.se han tomado cinco.
Ejemplo:Ejemplo:
Ptof.Chávez

17. FRACCIONES
COMO OPERADORES
Ptof.Chávez

18. A= 64
¿ Cuánto es un cuarto de 64 ?
Ptof.Chávez

19. A= 64
¼ de
64
¼ de 64 es igual a :16
( 1/4 ) 64= 16
Ptof.Chávez

20. Equivalencia
de fracciones
Ptof.Chávez

21. 1/2
4/8
8/16
16/32
½ = 4/8= 8/16= 16/32
Estas fracciones son equivalentes , ya que representan la misma porción de la unidad
Ptof.Chávez

22. Definición de fracciones
Equivalentes.
Ptof.Chávez

23. Dos fracciones a/b y c/d, son equivalentes
Si y solamente Si, ad = bc.
Así :
1/2 es equivalente a 2/4, ya que 1x4 = 2x2
1/2 es equivalente a 4/8, ya que 1x8=2x4
1/2 es equivalente a 8/16, ya que 1x16=2x8
1/2 es equivalente a 16/32, ya que 1x32=2x16
Ptof.Chávez

24. ORDEN EN LA
FRACCIONES
Ptof.Chávez

25. ¿ Qué es mayor 2/4 ó 3/4 ?
2/4
3/4
Puede observarse que 3/4 es mayor que 2/4
Ptof.Chávez

26. Orden de la fracción.
a/b es menor que c/d sí y solamente sí a x d es
menor que b x c.
Simbólicamente :
a/b < c/d ad < bc
Ptof.Chávez

27. Suma de FraccionesSuma de Fracciones
Metodología para la enseñanza de los números fraccionarios
HOMOGENEASHOMOGENEAS
Ptof.Chávez

28. Dibuja una cuadrícula de 4x4
• Colorea de naranja 1/4 de tu cuadrícula.
• Colorea 1/4 más de tu cuadrícula.
• ¿Qué parte de tu cuadrícula es toda la parte
coloreada? R/________
Entonces :1/4 + 1/4= _________?
Ptof.Chávez

29. •Colorea de naranja 1/8 de tu cuadrícula.
Colorea 1/8 más de tu cuadrícula.
¿Qué parte de tu cuadrícula es toda la parte
coloreada? R/________
Entonces :1/8 + 1/8= _________?
Dibuja otra cuadrícula de 4x4
Ptof.Chávez

30. • Colorea de naranja 1/16 de tu cuadrícula.
Colorea 3/16 más de tu cuadrícula.
¿Qué parte de tu cuadrícula es toda la parte
coloreada? R/________
Entonces :1/16 + 3/16= _________?
Dibuja otra cuadrícula de 4x4
Ptof.Chávez

31. ¿ Qué hacemos para sumar fracciones
de igual denominador ?
Ejemplo : 1/16 + 3/16 = 4/16
Ptof.Chávez

32. Para sumar fracciones de igual
denominador,solamente sumamos
los numeradores y dejamos el
mismo denominador.
Regla
Ptof.Chávez

33. 3/5 + 2/5 =
5
5
1
1
=
Ejemplo 1
Ejemplo 2
3/7 + 2/7 =
Ejemplo 3
2/8 + 4/8 =
6
8
3
4
=
1
5/7
3/4
Ptof.Chávez

34. Ejercicios.
Resolver:
7/9
7/11
10/15
a) 2/9 + 5/9 =
b) 2/11 + 5/11 =
c) 8/15 + 2/15 =
Ptof.Chávez

35. Suma de FraccionesSuma de Fracciones
Metodología para la enseñanza de los números fraccionarios
HETEROGENEASHETEROGENEAS
Ptof.Chávez

36. Miguel barrerá 1/2 de la cancha de baloncesto y
Carlos 2/6 .
¿ Qué cantidad de la cancha barrerán entre los
dos niños ?
PROBLEMA 1.PROBLEMA 1.
Ptof.Chávez

37. 1/2, Parte que barrerá
Miguel.
2/6, parte que
Barrerá Carlos.
1/2 + 2/6
= 3/6 + 2/6
= 5/6
Desarrollo
Ptof.Chávez

38. Problema 2
Para pintar un mueble se necesita 1/2 galón de
pintura verde, 1/4 de galón de pintura amarilla y
1/8 de galón de pintura color naranja.
¿ Qué cantidad de pintura se utilizará para pintar
el mueble ?
Ptof.Chávez

39. 8
DatosDatos
1/21/2 galón de pintura verde.
1/4 galón de pintura amarilla.
1/8 galón de pintura naranja.
Encontremos el m.c.m. de 2,4 y 8.
M . C . M. ( 2,4,8 ) =
Transformemos las fracciones a octavos
1/2 = 1/4 =
8
4
.
8
2
Ptof.Chávez

40. Ahora sumemos:
= 1/2 + 1/4 + 1/8 (Suma de heterogéneas )
=4/8 + 2/8 + 1/8 (suma de
homogéneas )
= 4 + 2 + 1 / 8
=7/8
De acuerdo a lo anterior para sumar fracciones
heterogéneas ,basta con transformarlas a fracciones
equivalentes y luego sumarlas como homogéneas.
Ptof.Chávez

41. Regla
Para sumar fracciones heterogéneas, encontramos el
mínimo común múltiplo de los denominadores ,que
será el denominador de la fracción resultante .El
m.c.m. Se divide entre cada uno de los denominadores
,este resultado se multiplica por el numerador y
luego se suman ,el total será el numerador de la
fracción resultante.
Ptof.Chávez

42. EjerciciosEjercicios
a) 1/2 + 1/4 =
2+ 1
4
=
3
4
b) 3/5 + 1/10 =
6 + 1
10
c) 4/9 + 2/3 =
4 + 6
9
7
10
=
=
10
9
Ptof.Chávez

43. d) 1/5 + 3/7 =
7 + 15
35
=
22
35
e) 3/4 + 1/5 + 3/10 =
15 + 4 + 6
20
=
25
20
=
5
4
5
4
Ptof.Chávez

44. Ptof.Chávez

45. Ptof.Chávez

46. ProblemaManuel tiene que barrer 4/6 de la cancha.
Si ya barrió 3/6 de la misma, ¿ Cuánto le falta
por barrer ?
4 sextos – 3 sextos = ( 4 – 3 ) sextos
= 1 sexto
Así ,
4/6 – 3/6 = 1/6
A Manuel le queda por barrer 1/6
Parte que tiene que barrer.
Ptof.Chávez

47. Otro ejemplo.
•Realizar : 2/3 –1/3
2 tercios – 1 tercio = ( 2 – 1 ) tercios.
= 1 tercio.
Así; 2/3 – 1/3 =
• Realizar: 3/9 – 2/9
3 novenos – 2 novenos = 1 noveno.
Así,
3/9 – 2/9 = 1/9
•Realizar : 7/10 – 2/10
7 décimos – 2 décimos = 5 décimos.
Así , 7/10 – 2/10 = 5/10
1/3
Ptof.Chávez

48. 1/5
Ejercicios
2/8
2/4
a) 2/5 – 1/5 =
c) 7/8 – 5/8 =
b) 3/4 – 1/4 =
d) 4 - 3/2 = 5/2
e) 7/10 – 5/10 = 1/5
f) 6/13 – 5/13 = 1/13
Ptof.Chávez

49. Ptof.Chávez