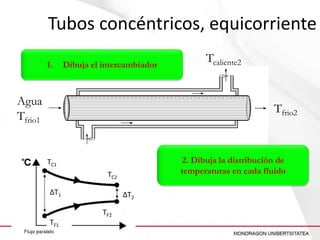
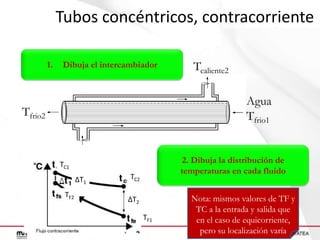
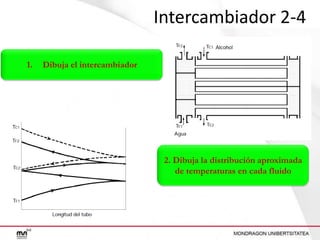
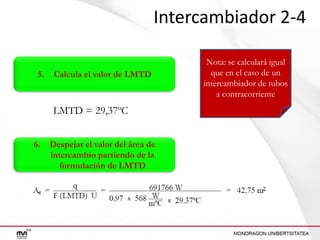
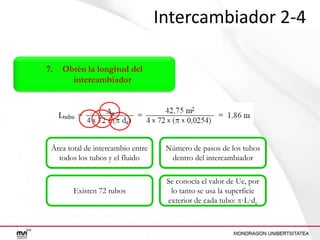
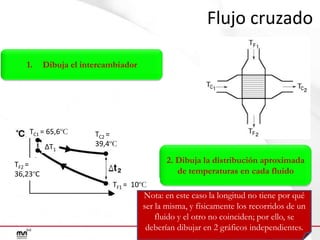
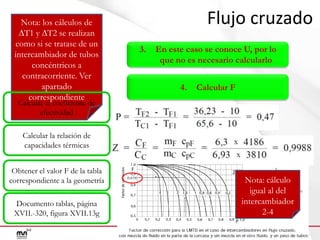
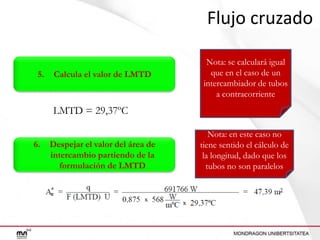
Este documento presenta un ejercicio para determinar el área de intercambio térmico necesaria para enfriar una solución de alcohol etílico utilizando agua en un intercambiador de calor. Se proporcionan cuatro configuraciones posibles para el intercambiador y se guía al lector a través de los cálculos necesarios para cada configuración, incluido el cálculo de temperaturas, calor transferido, LMTD y área de intercambio.

1. Diseño de intercambiadores mediante el
método LMTD
Ejercicio Guiado

2. Enunciado
Determinar el área de intercambio térmico que se necesita para
que un intercambiador de calor construido con un tubo de
25,4 mm de diámetro exterior, enfríe 6,93 kg/seg de una
solución de alcohol etílico al 95 % , cp=3.810 J/kg·K, desde
65,6°C hasta 39,4°C, utilizando 6,3 kg de agua por segundo a
10°C.
Se supondrá que el coeficiente global de transferencia térmica
basado en el área exterior del tubo es de 568 W/m·°C. El
problema se realizará en los siguientes supuestos
a) Carcasa y tubo con flujos en equicorriente
b) Carcasa y tubo con flujos en contracorriente
c) Intercambiador en contracorriente con dos pasos en carcasa y 4
pasos de tubos de 72 tubos en cada paso, circulando el alcohol
por la carcasa y el agua por los tubos
d) Flujo cruzado, con un paso de tubos y otro de carcasa, siendo
con mezcla de fluido en la carcasa.

3. metodología
Primeramente se debe identificar si se trata de un
ejercicio a resolver mediante el uso de la
metodología LMTD o mediante NTU
En el caso actual, dado que nos piden la longitud
del intercambiador, es decir, la geometría del
mismo, debemos usar la metodología LMTD

4. metodología
1. Obtener todas las temperaturas de entrada y salida,
caudales, etc. y el calor intercambiado
2. Obtener el valor del coeficiente global de
transmisión U
Cálculo de coeficientes de convección si fuesen necesarios
3. Calcular el factor corrector F, si fuese necesario (no
lo es en el caso de tubos simples a contracorriente o
equicorriente)
4. Obtener el valor de LMTD
5. Despejar el valor del área, y a partir del mismo la
longitud del intercambiador

5. Carcasa y tubo con flujos en
equicorriente
Carcasa y tubo con flujos en
contracorriente
Selecciona el apartado a resolver
Intercambiador en
contracorriente con 2 pasos en
carcasa y 4 pasos de tubos de
72 tubos en cada paso, (alcohol
por la carcasa, agua por los
tubos
Flujo cruzado, con un paso de
tubos y otro de carcasa,
siendo con mezcla de fluido
en la carcasa.

6. Tubos concéntricos, equicorriente
1.
Dibuja el intercambiador
Agua
Tfrio1
Tcaliente2
Tfrio2
TC1
Alcohol
Tcaliente1 TC2
∆T1
TF1
2. Dibuja la distribución de
temperaturas en cada fluido
∆T2
TF1
TF2

7. Tubos concéntricos, equicorriente
3.
Calcula ∆T1 y ∆T2
∆T2 = ∆TC1 – TF1 = 65,6 – 10 = 55,6ºC
∆T1 = ∆TC2 – TF2 = 39,4 – TF2
4.
Calcula el calor intercambiado
Transferencia de calor (no hay pérdidas),
Q = QC = QF = mC cpC (TC1 – TC2) = mF cpF (TF2 – TF1)
Q = 6,93 (kg/seg) x 3810 (J/kg.ºC) x (65,6 – 39,4)ºC =
= 6,3 (kg/seg) x 4186 (J/kg.ºC) x (TF2 – 10)ºC = 691.766 J/seg =
691,766 kW
5.
Obtén el valor de la temperatura
que falte; en este caso, TF2

8. Tubos concéntricos, equicorriente
6.
En este caso se conoce U, por lo
que no es necesario calcularlo
7. Al tratarse de 2 tubos simples
concéntricos, no es necesario calcular F
8.
Calcula el valor de LMTD
Nota: el valor de
LMTD ha de ser
un valor entre ∆T1
y ∆T2, ya que se
trata de una media
entre ambos valores

9. Tubos concéntricos, equicorriente
9.
Despejar el valor de la superficie de
intercambio de calor partiendo de
la fórmula de calor intercambiado
Nota: empleamos la superficie
exterior de los tubos, por ser el dato
conocido. Notar que se trata de la
superficie del tubo, no de su sección
Q  UA  F  LMTD
10. Obtener la longitud del intercambiador

10. fin del
ejercici
o
Regresar al resto de configuraciones

11. Tubos concéntricos, contracorriente
1.
Dibuja el intercambiador
Tcaliente2
Agua
Tfrio1
Tfrio2
Alcohol
TC1
Tcaliente1
∆T1
TF2
2. Dibuja la distribución de
temperaturas en cada fluido
TC2
∆T2
TF1
Nota: mismos valores de TF y
TC a la entrada y salida que
en el caso de equicorriente,
pero su localización varía

12. Tubos concéntricos, contracorriente
3.
Calcula ∆T1 y ∆T2
∆T2 = ∆TC1 – TF1 = 65,6 – 36,23 = 29,37ºC
∆T1 = ∆TC2 – TF2 = 39,4 – 10 = 29,4ºC
Nota: en esta ocasión hemos
Nota: de no haberlo hecho
4. Calcula el calor intercambiado
obtenido el valor de ∆T1 y ∆T2
así, desconoceríamos el valor de TF2
directamente, de que (no hay
por
Transferenciadadocalorlos valores pérdidas), lo que deberíamos de proceder a
de todas = temperaturas los hemos
pasos
Q = QC las QF = mC cpC (TC1 – TC2) = mF cpF (Tlos – TF1)4 y 5
F2
calculado en el caso de tubos
concéntricos equicorrientes
Q = 6,93 (kg/seg) x 3810 (J/kg.ºC) x (65,6 – 39,4)ºC =
= 6,3 (kg/seg) x 4186 (J/kg.ºC) x (TF2 – 10)ºC = 691.766 J/seg =
691,766 kW
5.
Obtén el valor de la temperatura
que falte; en este caso, TF2

13. Tubos concéntricos, contracorriente
6.
En este caso se conoce U, por lo
que no es necesario calcularlo
7. Al tratarse de 2 tubos simples
concéntricos, no es necesario calcular F
8.
Nota: el valor de
LMTD ha de ser
un valor entre ∆T1
y ∆T2, ya que se
trata de una media
entre ambos valores
Calcula el valor de LMTD
Nota: en este
caso, ∆T1 ≈ ∆T2;
por ello, LMTD =
∆T1 ≈ ∆T2, ya que
se trata de una
media entre ambos
valores

14. Tubos concéntricos, contracorriente
9.
Despejar el valor de la superficie de
intercambio de calor partiendo de
la fórmula de calor intercambiado
Nota: empleamos la superficie
exterior de los tubos, por ser el dato
conocido. Notar que se trata de la
superficie del tubo, no de su sección
Q  UA  F  LMTD
10. Obtener la longitud del intercambiador
519 m

15. fin del
ejercici
o
Regresar al resto de configuraciones

16. Intercambiador 2-4
1.
Dibuja el intercambiador
2. Dibuja la distribución aproximada
de temperaturas en cada fluido

17. Nota: los cálculos de
∆T1 y ∆T2 se realizan
como si se tratase de un
intercambiador de tubos
concéntricos a
contracorriente. Ver
apartado
correspondiente
Calcular el coeficiente de
efectividad
Calcular la relación de
capacidades térmicas
Obtener el valor F de la tabla
correspondiente a la geometría
Documento tablas, página
XVII.-319, figura XVII.13c
Intercambiador 2-4
3.
En este caso se conoce U, por lo
que no es necesario calcularlo
4.
Calcular F

18. Intercambiador 2-4
5.
Calcula el valor de LMTD
LMTD = 29,37ºC
6.
Despejar el valor del área de
intercambio partiendo de la
formulación de LMTD
Nota: se calculará igual
que en el caso de un
intercambiador de tubos
a contracorriente

19. Intercambiador 2-4
7.
Obtén la longitud del
intercambiador
Área total de intercambio entre
todos los tubos y el fluido
Número de pasos de los tubos
dentro del intercambiador
Existen 72 tubos
Se conocía el valor de Ue, por
lo tanto se usa la superficie
exterior de cada tubo: π·L·de

20. fin del
ejercici
o
Regresar al resto de configuraciones

21. Flujo cruzado
1.
Dibuja el intercambiador
TC1 = 65,6ºC
∆T1
TC2 =
39,4ºC
2. Dibuja la distribución aproximada
de temperaturas en cada fluido
TF2 =
36,23ºC
TF1 = 10ºC
Nota: en este caso la longitud no tiene por qué
ser la misma, y físicamente los recorridos de un
fluido y el otro no coinciden; por ello, se
deberían dibujar en 2 gráficos independientes.

22. Nota: los cálculos de
∆T1 y ∆T2 se realizan
como si se tratase de un
intercambiador de tubos
concéntricos a
contracorriente. Ver
apartado
correspondiente
Flujo cruzado
3.
En este caso se conoce U, por lo
que no es necesario calcularlo
4.
Calcular F
Calcular el coeficiente de
efectividad
Calcular la relación de
capacidades térmicas
Obtener el valor F de la tabla
correspondiente a la geometría
Documento tablas, página
XVII.-320, figura XVII.13g
Nota: cálculo
igual al del
intercambiador
2-4

23. Flujo cruzado
5.
Calcula el valor de LMTD
Nota: se calculará igual
que en el caso de un
intercambiador de tubos
a contracorriente
LMTD = 29,37ºC
6.
Despejar el valor del área de
intercambio partiendo de la
formulación de LMTD
Nota: en este caso no
tiene sentido el cálculo de
la longitud, dado que los
tubos no son paralelos

24. fin del
ejercici
o
Regresar al resto de configuraciones

25. gracias
www.mondragon.edu/muplus