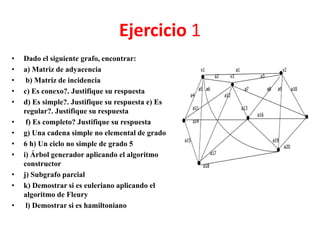
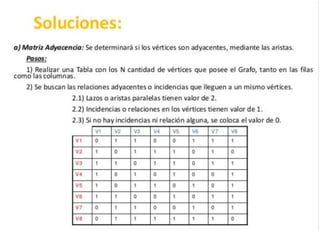
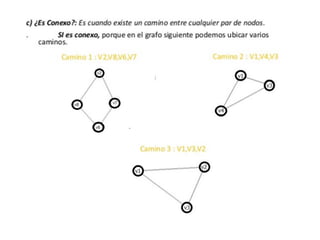
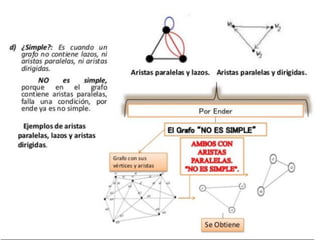
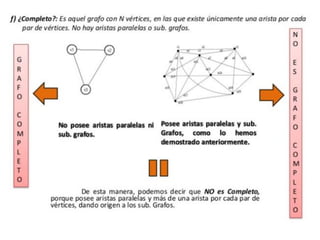
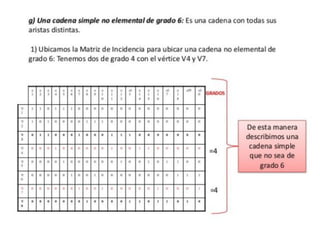
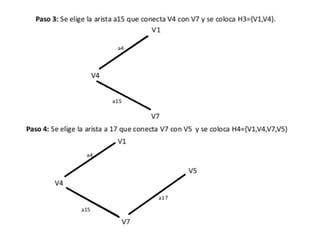
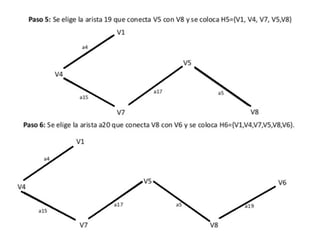
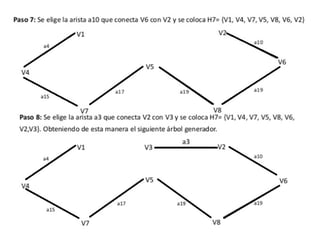
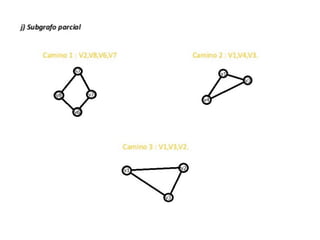
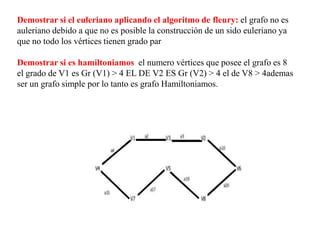
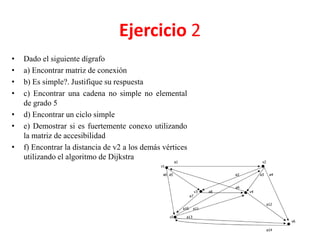
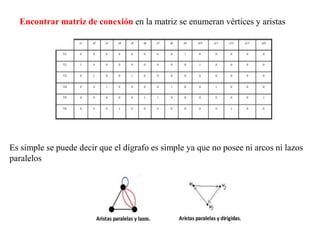
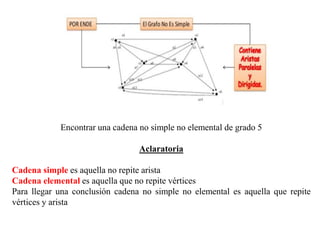
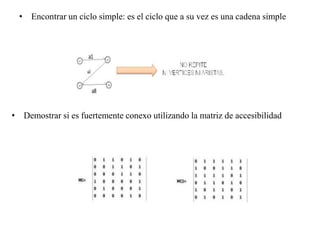
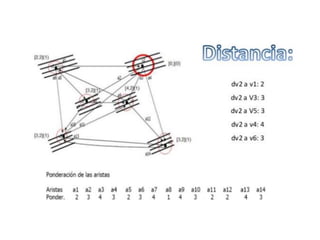
El documento presenta un ejercicio sobre grafos que incluye encontrar la matriz de adyacencia y de incidencia de un grafo, determinar si es conexo, simple, regular, completo, euleriano o hamiltoniano, encontrar una cadena y un ciclo, construir un árbol generador y un subgrafo parcial, y calcular distancias utilizando el algoritmo de Dijkstra. Se proveen detalles sobre cómo aplicar los algoritmos de Fleury y Dijkstra al grafo dado para resolver las preguntas planteadas.

1. Republica Bolivariana de Venezuela
Universidad “Fermín Toro”
Escuela de Ingeniería
Alumno
Jesús Sánchez CI: 21506130
Asignatura: Estructura Discreta
Sección: SAIA “B”
Prof. Edecio Freitez
Barquisimeto 03 de Agosto del 2017

2. Ejercicio 1
• Dado el siguiente grafo, encontrar:
• a) Matriz de adyacencia
• b) Matriz de incidencia
• c) Es conexo?. Justifique su respuesta
• d) Es simple?. Justifique su respuesta e) Es
regular?. Justifique su respuesta
• f) Es completo? Justifique su respuesta
• g) Una cadena simple no elemental de grado
• 6 h) Un ciclo no simple de grado 5
• i) Árbol generador aplicando el algoritmo
constructor
• j) Subgrafo parcial
• k) Demostrar si es euleriano aplicando el
algoritmo de Fleury
• l) Demostrar si es hamiltoniano

15. Demostrar si el euleriano aplicando el algoritmo de fleury: el grafo no es
auleriano debido a que no es posible la construcción de un sido euleriano ya
que no todo los vértices tienen grado par
Demostrar si es hamiltoniamos el numero vértices que posee el grafo es 8
el grado de V1 es Gr (V1) > 4 EL DE V2 ES Gr (V2) > 4 el de V8 > 4ademas
ser un grafo simple por lo tanto es grafo Hamiltoniamos.

16. Ejercicio 2
• Dado el siguiente dígrafo
• a) Encontrar matriz de conexión
• b) Es simple?. Justifique su respuesta
• c) Encontrar una cadena no simple no elemental
de grado 5
• d) Encontrar un ciclo simple
• e) Demostrar si es fuertemente conexo utilizando
la matriz de accesibilidad
• f) Encontrar la distancia de v2 a los demás vértices
utilizando el algoritmo de Dijkstra

17. Encontrar matriz de conexión en la matriz se enumeran vértices y aristas
Es simple se puede decir que el dígrafo es simple ya que no posee ni arcos ni lazos
paralelos

18. Encontrar una cadena no simple no elemental de grado 5
Aclaratoria
Cadena simple es aquella no repite arista
Cadena elemental es aquella que no repite vértices
Para llegar una conclusión cadena no simple no elemental es aquella que repite
vértices y arista

19. • Encontrar un ciclo simple: es el ciclo que a su vez es una cadena simple
• Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad

20. • Encontrar la distancia de V2 a los demás vértices utilizando el algoritmo de
dijkstra
Pasos
• Ubicar el vértice de inicio
• Luego ubicar los vértices mas cercanos al v2 para estudiarlos, lo que este
directamente a el
• Agregar etiquetas a cada vértice estudiado, la misma se realiza así.

21. • Luego de colocar la ponderación de la arista + la ponderación de la etiqueta
anterior que está directamente al vértice estudiado.
• Colocará al lado de la etiqueta el número de iteración que se está realizando
• Luego se estudian las distancia y se escoge la menor, si hay 2 iguales se escoge
cualquier
Pasos aplicados al grafo

23. Gracias por su atención