El documento presenta las soluciones a varios problemas sobre grafos planteados para un grafo dado. Incluye encontrar la matriz de adyacencia y de incidencia, determinar si el grafo es conexo, simple, regular, completo, y encontrar una cadena no elemental de grado 6, un ciclo no simple de grado 5, un árbol generador y demostrar si es euleriano o hamiltoniano. También plantea los mismos problemas pero para un dígrafo dado.

1. Universidad Fermín Toro
Vice-rectorado Académico
Faculta de Ingeniería
Escuela de Computacion
Cabudare, Estado Lara
Angel Nava C.I: 24.183.428
7/12/18

2. Dado el siguiente grafo, encontrar:
a)Matriz de adyacencia
b) Matriz de incidencia
c) Es conexo?. Justifique su respuesta
d) Es simple?. Justifique su respuesta
e) Es regular?. Justifique su respuesta
f) Es completo? Justifique su respuesta
g) Una cadena simple no elemental de grado 6
h) Un ciclo no simple de grado 5
i) Árbol generador aplicando el algoritmo constructor
j) Subgrafo parcial
k) Demostrar si es euleriano aplicando el algoritmo de fleury
l) Demostrar si es hamiltoniano

3. Solución
a) Matriz de Adyacencia
Ma (G)=
b) Matriz de Incidencia
Mi (G) =
V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 0 6 1 1
V2 1 0 1 0 1 1 0 1
V3 1 1 0 1 1 1 1 0
V4 1 0 1 0 1 0 1 0
V5 0 1 1 1 0 1 1 1
V6 0 1 1 0 1 0 0 1
V7 1 0 1 1 1 0 0 1
V8 1 1 0 0 1 1 1 0
V1 V2 V3 V4 V5 V6 V7 V8
A1 1 1 0 0 0 0 0 0
A2 1 0 1 0 0 0 0 0
A3 0 1 1 0 0 0 0 0
A4 1 0 0 1 0 0 0 0
A5 1 0 0 0 1 0 0 0
A6 1 0 0 0 0 0 1 0
A7 0 0 1 0 0 0 0 1
A8 0 1 0 0 0 1 0 0
A9 0 1 0 0 0 0 1 0
A10 0 1 0 0 0 0 0 1
A11 0 0 1 1 0 0 0 0
A12 0 0 1 0 1 0 0 0
A13 0 0 1 0 0 1 0 0
A14 0 0 0 1 0 1 0 0
A15 0 0 0 1 1 0 0 0
A16 0 0 0 0 0 1 0 1
A17 0 0 0 0 1 1 0 0
A18 0 0 0 0 1 0 1 0
A19 0 0 0 0 0 1 1 0
A20 0 0 0 0 0 0 1 1

4. Es conexo?
Si es Conexo, ya que según la definición, nos dice que para cualquier par de
vértices a y b en (G) existe al menos una trayectoria de (a) a (b) donde tienen un
camino que los une.
Es Simple?
Si es simple, ya que no posee lazos en ninguno de sus vértices.
Es Regular?
Para que sea regular deben poseer los mismos grados y en este caso, No es
regular, ya que no todos sus vértices tienen los mismos grados, como:
V1= 5, V2= 5, V3= 6, V4= 4, V5= 6, V6= 4, V7= 5, V8= 5
Es Completo?
No es completo, ya que no cumple con la definición de una arista pues, no existen
vértices, digamos (V1 y V6) no posee ninguna arista que los conecte.
Una cadena simple no elemental de grado 6
C=[v1 a1 v2 a10 v6 a16 v5 a14 v4 a11 v3 a3 v2] Nos indica que no es elemental,
ya que repite el vértice [v2]
Un ciclo no simple de grado 5
C= [v5 a19 v8 a18 v7 a17 v5 a19 v7 a9 v2] Nos indica que no es simple, porque
repite la arista [a19].
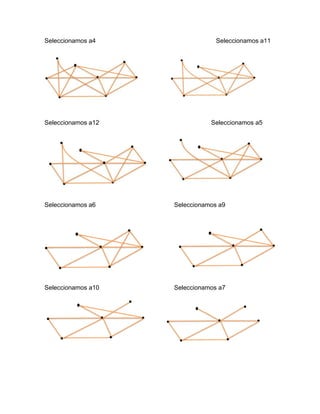
Árbol generador aplicando el algoritmo constructor
• Elegimos S1=V1 Haciendo H1=[V1]
• Elegimos la arista A4 que conecta a V1 con V4 haciendo H2=[v1,v4]

5. Elegimos la arista a15 que conecta a V4 con V7 haciendo H3=[v1 v4 v7]
Eligimos la arista a17 que coneta a V7 con V5 haciendo H4[v1 v4 v5]
Elegiremos la arista A19 que conecta a V5 con V8 haciendo
H5=[v1 v4 v8]
Elegiremos la arista A20 que conecta V8 con V6 haciendo H6=[V1
v4 v7 v5 v8 v6]

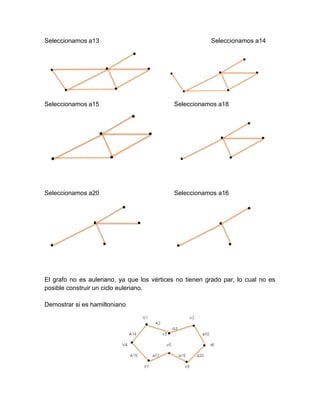
6. Elegiremos la arista A10 que conecta a V6 con V2 haciendo
H7=[v1 v4 v7 v5 v8 v6 v2]
Elegiremos la arista A3 que conecta a v2 con v3 haciendo H8=[v1 v4 v7 v5 v8 v6
v2 v3]
Árbol Generador
Subgrafo parcial

7. Demostrar si es euleriano aplicando el algoritmo de Fleury
Seleccionamos a1
Seleccionamos a3 Seleccionamos a2

8. Seleccionamos a4 Seleccionamos a11
Seleccionamos a12 Seleccionamos a5
Seleccionamos a6 Seleccionamos a9
Seleccionamos a10 Seleccionamos a7

9. Seleccionamos a13 Seleccionamos a14
Seleccionamos a15 Seleccionamos a18
Seleccionamos a20 Seleccionamos a16
El grafo no es auleriano, ya que los vértices no tienen grado par, lo cual no es
posible construir un ciclo euleriano.
Demostrar si es hamiltoniano

10. Es Hamiltoniano ya que el número de vértices de G en 8, Gr (v1) ≥ 8/2=4 (i=1,2,8)
Dado el siguiente dígrafo
a)Encontrar matriz de conexión
b)Es simple? Justifique su respuesta
c)Encontrar una cadena no simple no elemental de grado 5
d)Encontrar un ciclo simple
e)Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad
f)Encontrar la distancia de v2 a los demás vértices utilizando el algoritmo de
Dijkstra
a) Encontrar matriz de conexión
b) Es simple? Justifique su respuesta
El dígrafo si es simple, porque no tiene ningún lazo y tampoco

11. existen arcos paralelos que puedan partir de un mismo vértice a
otro.
c) Encontrar una cadena no simple no elemental de grado 5
d) Encontrar un ciclo simple
e) Demostrar si es fuertemente conexo utilizando la matriz de
accesibilidad

13.  Componentes iguales a cero (0) permanecerá como cero (0)
 Componentes diferentes de cero (0) se convertirá en uno (1)
Dígrafo Fuertemente Conexo

14. f)Encontrar la distancia de v2 a los demás vértices utilizando el
algoritmo de Dijkstra
Ponderación de las aristas
Aristas a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12
a13 a14
Ponder. 2 3 4 3 2 3 4 1 4 3 2 2 4 3