El documento presenta un análisis de grafos y dígrafos realizado por un estudiante. Contiene la resolución de varios ejercicios sobre un grafo dado, incluyendo encontrar su matriz de adyacencia y de incidencia, determinar si es conexo, simple, regular o completo, y encontrar cadenas, ciclos y un árbol generador. También analiza un dígrafo dado y resuelve ejercicios similares sobre él.

1. Universidad Fermín toro
Decanato de ingeniería.
Ejercicios de grafos y dígrafos
Alumno: Aron Boza
C.I:23.537.620
Prof. Edecio Freites
Asignatura: Estructura discreta 2

2. Dado el siguiente grafo, encontrar:
a) Matriz de adyacencia.
V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 0 0 1 1
V2 1 0 1 0 1 1 0 1
V3 1 1 0 1 1 1 1 0
V4 1 0 1 0 1 0 1 0
V5 0 1 1 1 0 1 1 1
V6 0 1 1 0 1 0 0 1
V7 1 0 1 1 1 0 0 1
V8 1 1 0 0 1 1 1 0
b) Matriz de incidencia
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15 a16 a17 a18 a19 A20
V1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
V2 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
V3 0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0
V4 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
V5 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0
V6 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
V7 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 1 0 0
V8 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
c) ¿Es conexo? Justifique su respuesta
Si es conexo, ya que todos los vértices están conectados por una arista.
d) ¿Es simple? Justifique su respuesta
V4
V6
V5
V8
V7

3. Si es simple, ya que no contiene lazos en los vértices.
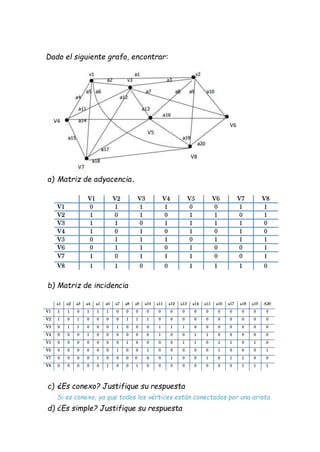
e) ¿Es regular? Justifique su respuesta
No es regular, ya que los vértices poseen distintos grados.
Ejemplo: el vértice V1 es de grado 5, y el vértice V3 es de grado
6.
f) ¿Es completo? Justifique su respuesta
No es completo, ya que existen un par de vértices distintos que no son
unidos por una misma arista, como por ejemplo, v3,v7…v1,v6…v3,v8.
g) Una cadena simple no elemental de grado 6
Una cadena simple es una secuencia finita alternada de vértices y
aristas, sin repetir aristas, no elemental indica que puede repetirse los
vértices. El grado nos indica la cantidad de aristas que debe contener la
cadena, e esta oportunidad son seis (6).
C: [V7,a15,V4, a11,V3,a7,V6,a16,V5,a19,V8,a18,V7]
h) Un ciclo no simple de grado 5
Un ciclo no simple es aquel donde las aristas pueden repetirse. El grado
nos indica el número de aristas que debe tener el ciclo, e esta
oportunidad son cinco (5)
C: [V2, a10 V6, a20,V8, a19,V5, a16,V6, a10,V2]
i) Árbol generador aplicando el algoritmo
constructor 1 er Paso: seleccione un vértice S1,
hacer H1= { S1}
2do Paso: Seleccione una arista a1 que tenga un extremo en H1 y el otro
extremo en un vértice S2 H1 hacer H1 {S2}
3er Paso: seleccionamos una arista a2 que tenga un extremo en H2 y el
otro extremo en un vértice S3 H2 hacer H2 {S3}
V1
Seleccionamos el vértice v1 H1= { S1}
Seleccionamos la arista a4 H2= { v1, v4}
a4
V4

4. V1
V3
V4
V7
A H3 = {v1, v4, v7}
A H4 = {v1, v4, v7, v3}
A H5 = {v1, v4, v7, v3, v5} V5
A H6 = {v1, v4, v7, v3, v5, v2}
A H7 = { v1, v4, v7, v3, v5, v2, v6}
V4
A H8 = { v1, v4, v7, v3, v5, v2, v6,
v8}
V1
V3 V2
V5
V7
V6
V8
Por lo tanto, se comprueba que en un árbol, dos vértices cualquiera están
unidos por un único camino, se demuestra con al poseer árbol generador que
es un grafo conexo y que G es un árbol, entonces el número de aristas de es
igual al número de vértices menos 1.
A = {a4, a15, a12, a3, a8, a10, a20}
V = {v1, v4, v7, v3, v5, v2, v6, v8}
Numero de vértices = 8 - 1 = 7
Numero de aristas = 7
V1
V3 V2
V4 V5
V7
V6

5. j) Subgrafo parcial
Un subgrafo parcial se obtiene al conservar todos los nodos o vértices
de G y se suprimen algunas aristas.
Tenemos:
V1
V2
V7 V8
k) Demostrar si es Euleriano aplicando el algoritmo de Fleury
Si el grafo es euleriano a partir de un vértice cualquiera de G se puede
construir una cadena simple de manera que no se repitan las aristas y no
se elijan aristas de corte a no ser que no se encuentre otra alternativa,
al haber agotado las aristas decimos que tenemos un tour euleriano.
Luego de experimentar en repetidas ocasiones el recorrido del grafo sin
repetir aristas, no ha sido posible encontrar un camino euleriano donde
no se repitan aristas, por lo tanto no se cumple que el Grafo sea
Euleriano.
V3
a2 A3
V4
V5
V6
a19
a15 a20
a17

6. l) Demostrar si es Hamiltoniano
Un grafo es hamiltoniano si contiene un ciclo hamiltoniano, en el cual
se debe cumplir que atraviese cada vértice del grafo exactamente
una vez.
el ciclo C=
Notamos que Vo = Vk
V1
V7 V8
Dado el siguiente dígrafo
a3 V2
a2
V3 a10
a11
V5
V4
V6
a19
a15 a20
a17

7. a) Encontrar matriz de conexión
Mc(G)=
b) ¿Es simple? Justifique su repuesta.
Se cumple que el Dígrafo es simple, tal que no tiene lazos y no
existen arcos paralelos que partan de un mismo vértice a otro.
c) Encontrar una cadena no simple no elemental de grado 5.
En las cadenas no simples se pueden repetir los arcos durante
el recorrido y que sea no elemental, también nos permite
repetir vértices. El grado 5 nos indica el número de arcos que
tendrá nuestra cadena.
T =
d) Encontrar un ciclo simple
El ciclo simple inicia y termina con el mismo vértice y en ella no se
pueden repetir arcos.
C =
e)Demostrar si es fuertemente conexo utilizando la matriz de
accesibilidad.
Para comprobar que un grafo es conexo podemos realizar los siguientes pasos:
1) Hallar la matriz de adyacencia y se eleva a la enésima potencia.
2) Se calcula la suma de las potencias de A hasta An.
3) Si todos sus elementos son distintos de cero, el grafo es conexo.
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0

8. Matriz de Adyacencia
Ma(D)=
Elevamos la matriz al cuadrado para encontrar los caminos de
tamaño dos (02)
(D)=
Elevamos la matriz al cubo para encontrar los caminos de tamaño tres (03)
(D)=
Elevamos la matriz a cuatro para encontrar los caminos de tamaño
cuatro (04)
(D)=
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
V1 V2 V3 V4 V5 V6
V1 0 0 1 1 1 1
V2 1 0 0 1 1 1
V3 1 1 0 1 0 1
V4 0 1 1 0 1 0
V5 1 0 1 1 1 1
V6 0 1 0 1 0 1
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 0 1 1
V4 0 1 1 1 1 1
V5 0 1 1 1 1 1
V6 1 0 1 1 0 1
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 0 1 1 1 1
V3 0 1 1 1 1 1
V4 1 1 0 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1

9. Elevamos la matriz a cinco para encontrar los caminos de tamaño
cinco (05)
(D)=
Ahora calculamos la matriz de accesibilidad
Acc(D) = bin
Acc (D)=bin
Luego transformamos la matriz de la manera siguiente:
a) Componente que sea igual a cero (0), permanece como (0)
b) Componente diferente de cero (0), convertirla a 1.
Acc (D)=bin
Como la matriz Acc(D) no tiene componentes nulas se dice entonces según
el colorido 1.2 que el dialogo es fuertemente conexo.
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 1 1 1
V4 1 1 1 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1
V1 V2 V3 V4 V5 V6
V1 3 4 5 4 5 4
V2 4 2 5 5 5 5
V3 3 4 3 4 4 4
V4 4 4 3 5 4 4
V5 3 4 4 5 4 5
V6 3 3 3 4 1 4
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 1 1 1
V4 1 1 1 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 1 1

10. f) Encontrar la distancia de v2 a los demás vértices
utilizando el algoritmo de Dijkastra
Ponderación de las aristas
Aristas a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
Ponder. 2 3 4 3 2 3 4 1 4 3 2 2 4 3
dv 2 a v1= 2
dv 2 a v1= 3
dv 2 a v4= 4
dv 2 a v5= 3
dv 2 a v6= 3