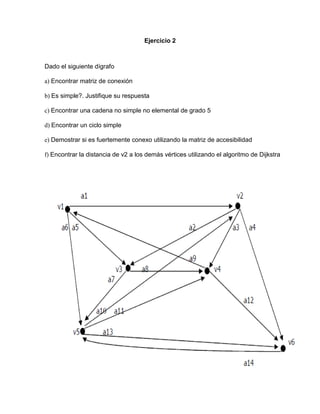
Este documento presenta una serie de ejercicios sobre estructuras discretas II. En el ejercicio 1, se pide analizar un grafo dado encontrando su matriz de adyacencia y de incidencia, determinar si es conexo, simple, regular, completo, y demostrar la existencia de una cadena y un ciclo. En el ejercicio 2, se pide realizar análisis similares sobre un digrafo, incluyendo determinar si es fuertemente conexo y encontrar distancias utilizando el algoritmo de Dijkstra.

1. REPUBLICA BOLIVARIANA DE VENEZUELA
MINISTERIO DEL PODER POPULAR PARA LA EDUCACION
UNIVERSIDAD FERMIN TORO
CABUDARE
Ejercicios Propuestos:
ESTRUCTURAS DISCRETAS II
NEUDO FREITE
V-18.922.725
SAIA : B

2. v5
v7
Ejercicio 1
Dado el siguiente grafo, encontrar:
a) Matriz de adyancencia.
b) Matriz de incidencia.
c) Es conexo?. Justifique su respuesta.
d) Es simple?. Justifique su respuesta.
e) Es regular?. Justifique su respuesta.
f) Es completo? Justifique su respuesta.
g) Una cadena simple no elemental de grado 6.
h) Un ciclo no simple de grado 5.
i) Arbol generador aplicando el algoritmo constructor.
j) Subgrafo parcial.
k) Demostrar si es euleriano aplicando el algoritmo de Fleury.
l) Demostrar si es hamiltoniano.
v4 v6
v8

3. Solución 1
a) Matriz de adyacencia:
Ma=G
b) Matriz de incidencia:
a1 a2 a
3
a4 a5 a6 a7 a8 a
9
a1
0
a1
1
a1
2
a1
3
a1
4
a1
5
a1
6
a1
7
a1
8
a1
9
a2
0
V1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
V2 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
V3 0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0
V4 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
V5 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0
V6 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
V7 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
V8 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 1 0 0
0 1 1 1 0 0 1 1
1 0 1 0 1 1 1 0
1 1 0 1 1 1 0 1
1 0 1 0 1 0 0 1
0 1 1 1 0 1 1 1
0 1 1 0 1 0 1 0
1 1 0 0 1 1 0 1
1 0 1 1 1 0 1 0

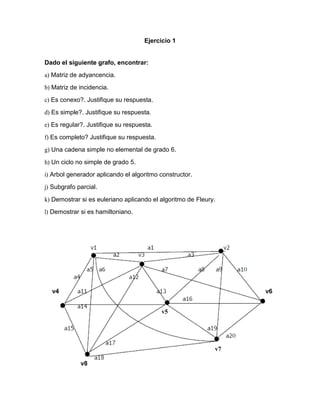
4. c) Es conexo?. Justifique su respuesta.
Si, ya que todos sus vértices están conectados entre si.
d) Es simple?. Justifique su respuesta.
Es simple ya que el grafo no tiene lazos en ninguno de sus vértices y para cada
par de de vértices distintos solo existe una arista.
e) Es regular?. Justifique su respuesta.
No lo es ya que todos sus vértices no tienen el mismo
grado. gr(v1)= 5
gr(v2)= 5
gr(v3)= 6
gr(v4)= 4
gr(v5)= 6
gr(v6)= 4
gr(v7)= 5
gr(v8)= 5
f) Es completo? Justifique su respuesta.
No es completo ya que no cumple con la definición de una arista por cada par de
vértices. (entre v1 y v5 no hay ninguna arista que los conecte).
g) Una cadena simple no elemental de
grado 6. C1 =
[V1,a1,V2,a10,V6,a20,V7,a19,V5,a13,V3,a3,V2]
h) Un ciclo no simple de grado 5.
C2 = [V1,a2,V3,a12,V8,a15,V4,a4,V1,a2,V3]

5. i) Arbol generador aplicando el algoritmo constructor.
Seleccionar Vértice V1, H1 = {V1}
arista 1 y H2= {V1,V2}
arista 10 y H3= {V1,V2,V6}
arista 20 y H4= {V1,V2,V6,V7}
arista 19 y H5= {V1,V2,V6,V7,V5}

6. arista 13 y H6= {V1,V2,V6,V7,V5,V3}
arista 12 y H7= {V1,V2,V6,V7,V5,V3,V8}
arista 15 y H8= {V1,V2,V6,V7,V5,V3,V8,V4}

7. j) Subgrafo parcial.
k) Demostrar si es euleriano aplicando el algoritmo de Fleury.
Seleccionamos a1
Seleccionamos a3

8. Seleccionamos a2
Seleccionamos a4
Seleccionamos a11
Seleccionamos a12

9. Seleccionamos a5
Seleccionamos a6
Seleccionamos a9
Seleccionamos a10

10. Seleccionamos a7
Seleccionamos a13
Seleccionamos a14
Seleccionamos a15

11. Seleccionamos a18
Seleccionamos a20
Seleccionamos a16
El grafo no es euleriano según el algoritmo de Fleury.
Se debe tomar en cuenta que un grafo es euleriano sólo si no tiene vértices de
grado impar y este no lo es ya que varios de sus vértices son de grado impar.

12. l) Demostrar si es hamiltoniano.
Existe un camino hamiltoniano ya que se puede pasar por cada vértice una vez sin
repetir ninguno.
Cadena hamiltoniano V1, V3, V2, V6, V7, V5, V8,
V4 Existe también un ciclo hamiltoniano.
Ciclo hamiltoniano V1, V3, V2, V5, V6, V7, V8, V4, V1
Por lo tanto el grafo dado si es hamiltoniano.

13. Ejercicio 2
Dado el siguiente dígrafo
a) Encontrar matriz de conexión
b) Es simple?. Justifique su respuesta
c) Encontrar una cadena no simple no elemental de grado 5
d) Encontrar un ciclo simple
e) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad
f) Encontrar la distancia de v2 a los demás vértices utilizando el algoritmo de Dijkstra

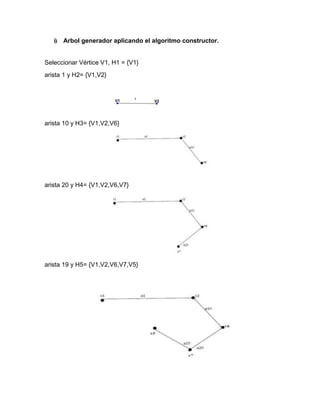
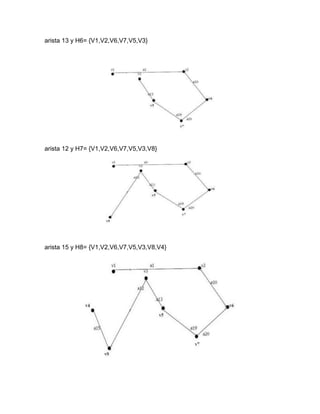
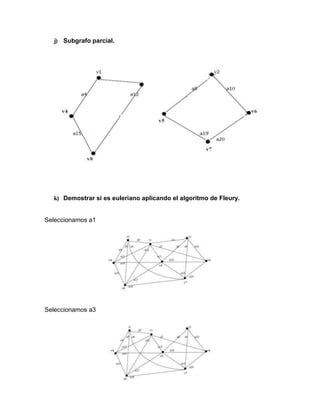
14. Solucion 2
a) Encontrar matriz de conexión
b)
McD=
c) Es simple?. Justifique su respuesta
Si, es simple ya que no tiene lazos ni arcos paralelos.
d) Encontrar una cadena no simple no elemental de grado 5
T1=[V4,a12,V6,a14,V5,a10,V2,a4,V6,a14,V5]
e) Encontrar un ciclo simple
C1=[V1,a6,V5,a13,V6,a14,V5,a11,V4,a9,V1]
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0

15. f) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad
McD=
M2=
M3=
M4=
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
0 1 1 1 1 1
1 0 0 1 1 1
1 1 0 1 0 1
0 1 1 0 1 0
1 0 1 1 1 1
0 1 0 1 0 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
0 1 1 1 1 1
1 1 1 1 1 1
1 0 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1

16. M5=
M6=
Mi=
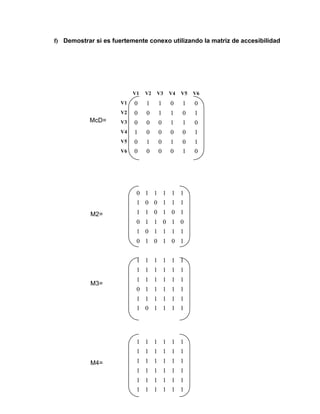
Finalmente Acc(D)= bin=[I7 + M+M2+M3+M4+M5+M6]
31 40 33 65 62 79 1 1 1 1 1 1
22 33 24 47 47 58 1 1 1 1 1 1
20 26 22 39 43 49 = 1 1 1 1 1 1
16 29 21 42 38 48 1 1 1 1 1 1
23 34 25 49 53 60 1 1 1 1 1 1
11 14 12 23 23 30 1 1 1 1 1 1
Como la matriz de accesibilidad no tiene componentes nulos se puede afirmar que el
dígrafo es fuertemente conexo.
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1

17. g) Encontrar la distancia de v2 a los demás vértices utilizando el
algoritmo de Dijkstra
=[8,4](3
)
=[0,-](0)
=[3,2](1)
=[4,2](1
)
=[4,3](2)
=[7,3](2)
=[6,6](4) =[3,2](1)
D v2 a v1 =
8 D v2 a v3
= 3 D v2 a
v4 = 4 D v2
a v5 = 6 D
v2 a v6 = 3