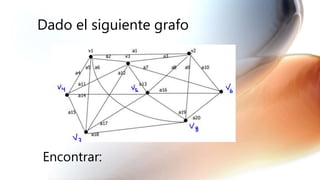
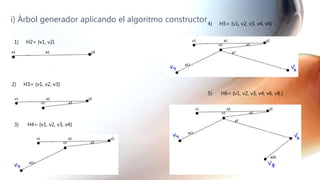
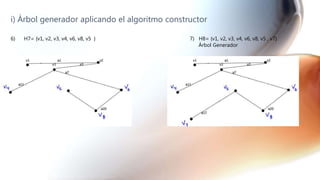
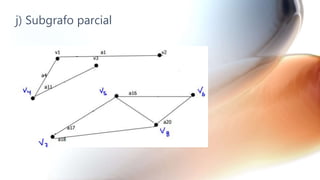
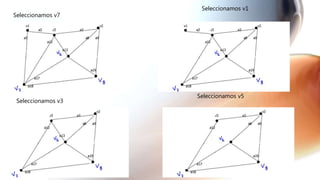
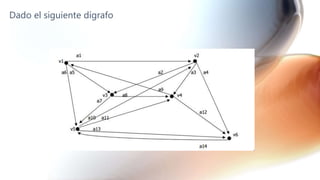
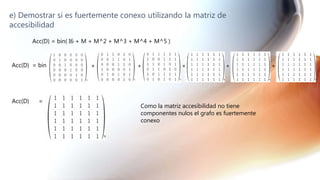
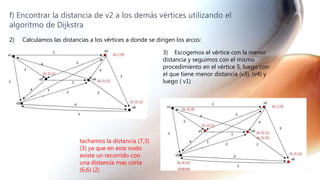
El documento presenta una serie de ejercicios sobre grafos y dígrafos, incluyendo encontrar la matriz de adyacencia y de incidencia, determinar si son conexos, regulares, completos o eulerianos, encontrar cadenas, ciclos, árboles generadores y aplicar algoritmos como el de Dijkstra.

1. EJERCICIOS PROPUESTOS
UNIVERSIDAD FERMIN TORO
DEPARTAMENTO DE MATEMATICAS
ESTRUCTURAS DISCRETAS II

2. Dado el siguiente grafo
Encontrar:

3. a) Matriz de adyacencia
Ma(G) =

4. b) Matriz de incidencia
a1
a2
a3
a4
a5
a6
a7
a8
a9
a10
a11
a12
a13
a14
a15
a16
a17
a18
a19
a20
v1 v2 v3 v4 v5 v6 v7 v8

5. c) Es conexo?. Justifique su respuesta
El grafo es un grafo conexo, dado que se pueden conseguir
cadenas con todos los vértices del grafo, es decir, todos se
comunican entre si, existe una trayectoria de cualquier vértice a
otro.
d) Es simple?. Justifique su respuesta
El grafo es simple porque no posee aristas lazo y existe solo una arista
que comunica cada par de vértices

6. e) Es regular?. Justifique su respuesta
No es grafo regular ya que sus vértices no son todos del mismo
grado, por ejemplo, v1 es de grado 5, mientras que v3 es de grado 6.
f) Es completo? Justifique su respuesta
No es grafo completo ya que no hay una arista entre cada vértice, por
ejemplo, no hay una arista con extremos en v2 y v4.

7. g) Una cadena simple no elemental de grado 6
C1= (v1, a1, v2, a3, v3, a11, v4, a14, v5, a13, v3, a7, v6)
h) Un ciclo no simple de grado 5
C2= (v3, a7, v6, a16, v5, a19, v8, a20, v6, a7,v3)

8. i) Árbol generador aplicando el algoritmo constructor
1) H2= {v1, v2}
2) H3= {v1, v2, v3}
3) H4= {v1, v2, v3, v4}
4) H5= {v1, v2, v3, v4, v6}
5) H6= {v1, v2, v3, v4, v6, v8 }

9. i) Árbol generador aplicando el algoritmo constructor
6) H7= {v1, v2, v3, v4, v6, v8, v5 } 7) H8= {v1, v2, v3, v4, v6, v8, v5 , v7}
Árbol Generador

10. j) Subgrafo parcial

11. k) Demostrar si es euleriano aplicando el algoritmo de Fleury
seleccionamos v1 seleccionamos v2

12. Seleccionamos v6
Seleccionamos v4
Seleccionamos v3
Seleccionamos v5

13. Seleccionamos v6 Seleccionamos v8
Seleccionamos v1
Seleccionamos v4

14. Seleccionamos v7
Seleccionamos v1
Seleccionamos v3
Seleccionamos v5

15. Seleccionamos v7 Seleccionamos v3
Seleccionamos v2
Seleccionamos v2

16. Seleccionamos v8 Seleccionamos v2
Así, el grafo no es euleriano, ya que queda una arista fuera de la cadena, además, mas de dos
aristas del grafo son de grado impar, lo que impide que sea un grafo euleriano

17. l) Demostrar si es hamiltoniano
El grafo es hamiltoniano al tener un ciclo hamiltoniano

18. Dado el siguiente dígrafo

19. a) Encontrar matriz de conexión
McD =

20. b) Es simple?. Justifique su respuesta
Es simple ya que no tiene lazos ni arcos paralélos
c) Encontrar una cadena no simple no elemental de grado 5
C1 = ( v1, a1, v2, a2, v3, a8, v4, a9, v1, a6, v5)
d) Encontrar un ciclo simple
C2= (v1, a1, v2, a4, v6, a14, v5, a11, v4, a9, v1)

21. e) Demostrar si es fuertemente conexo utilizando la matriz de
accesibilidad
Acc(D) = bin( I6 + M + M^2 + M^3 + M^4 + M^5 )
+ + + + += bin
=
Acc(D)
Acc(D)
Como la matriz accesibilidad no tiene
componentes nulos el grafo es fuertemente
conexo

22. f) Encontrar la distancia de v2 a los demás vértices utilizando el
algoritmo de Dijkstra
1) Empezamos en el vértice v2 colocando la distancia acumulada “0” seguido del vértice de donde
proviene (ninguno al ser el primero), luego se coloca el recorrido:
(distancia, vértice anterior) (recorrido)

23. f) Encontrar la distancia de v2 a los demás vértices utilizando el
algoritmo de Dijkstra
2) Calculamos las distancias a los vértices a donde se dirigen los arcos:
3) Escogemos el vértice con la menor
distancia y seguimos con el mismo
procedimiento en el vértice 5, luego con
el que tiene menor distancia (v3), (v4) y
luego ( v1)
tachamos la distancia (7,3)
(3) ya que en este nodo
existe un recorrido con
una distancia mas corta
(6,6) (2)

24. f) Encontrar la distancia de v2 a los demás vértices utilizando el
algoritmo de Dijkstra
4) Finalmente se siguen los mismos pasos en los vértices v1 y v5, pero no se agregan distancias ya que estas
son mas largas que las que ya calculamos.
Así, las mejores distancias de v2 a los otros vértices son:
d(2 a 6) = 3 recorriendo 2 6
d(2 a 4) = 4 recorriendo 2 4
d(2 a 3) = 3 recorriendo 2 3
d(2 a 5) = 6 recorriendo 2 6 5
d(2 a 1) = 8 recorriendo 2 4 1