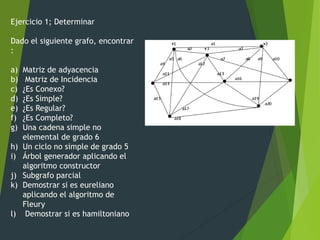
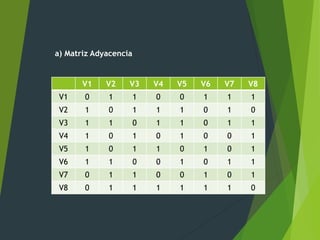
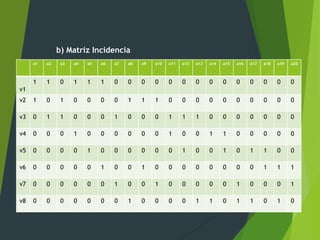
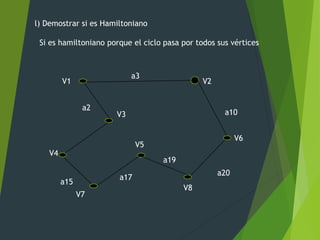
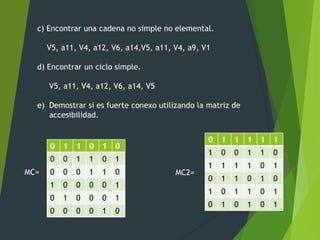
El documento presenta un ejercicio de estructuras sobre grafos no dirigidos y dirigidos. Se pide determinar la matriz de adyacencia, incidencia, conectividad, ciclos, árbol generador y otros atributos. También se analiza un dígrafo con ponderación de aristas para encontrar su matriz de conexión, cadenas, ciclos y fuerte conectividad.

1. UNIVERSIDAD FERMÍN TORO
VICERECTORADO ACADÉMICO
DECANATO DE INGENIERÍA
ESCUELA DE INGENIERÍA EN COMPUTACION
ESTRUCTURAS
DISCTRAS II
Alumno:
José Antonio Salas Meléndez 23.835.999

2. Ejercicio 1; Determinar
Dado el siguiente grafo, encontrar
:
a) Matriz de adyacencia
b) Matriz de Incidencia
c) ¿Es Conexo?
d) ¿Es Simple?
e) ¿Es Regular?
f) ¿Es Completo?
g) Una cadena simple no
elemental de grado 6
h) Un ciclo no simple de grado 5
i) Árbol generador aplicando el
algoritmo constructor
j) Subgrafo parcial
k) Demostrar si es eureliano
aplicando el algoritmo de
Fleury
l) Demostrar si es hamiltoniano

3. V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 0 0 1 1 1
V2 1 0 1 1 1 0 1 0
V3 1 1 0 1 1 0 1 1
V4 1 0 1 0 1 0 0 1
V5 1 0 1 1 0 1 0 1
V6 1 1 0 0 1 0 1 1
V7 0 1 1 0 0 1 0 1
V8 0 1 1 1 1 1 1 0
a) Matriz Adyacencia

4. a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15 a16 a17 a18 a19 a20
v1
1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
v2 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
v3 0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0
v4 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
v5 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 1 0 0
v6 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
v7 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
v8 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0
b) Matriz Incidencia

5. c) ¿Es Conexo?
Si es que conexo, ya que todos los vértices están
conectados a través de al menos una trayectoria
d) ¿Es Simple?
Si es simple porque cada par de vértices distintos están
conectados con una única arista.
e) ¿Es Regular?
No es regular porque los vértices no poseen el mismo
grado
f) ¿Es Completo?
No es completo porque aristas paralelas y mas de una
arista por cada para de vértices, dando origen a los
subgrafos

6. g) Una cadena simple no elemental de grado 6
{ V3, a13, V5,a16, V6,a20, V8,
a19,V5,a14,V4,a15,V7}
h) Un ciclo no simple de grado 5
Ya que todas las aristas son distintas del grafo. No
hay cadenas simples de ningún grado, por lo tanto no
se puede demostrar.
i) Árbol generador usando el algoritmo constructor
Paso 1 : Elegir V1, y coloca H1={V1}
Paso 2: Se elige a1 entonces H2={V1,V2}
V1
V1 V2
a1

7. Paso 3: se elige la arista a3 entonces se coloca
H3={V1,V2,V3}
V1 V2
a1
V3
a3
Paso 4: Se elige la arista a11 entonces se coloca H4= {V1,V2,V3,V4}
V1 V2
V3
a3
V4
a11
a1

8. Paso 5: Se elige la arista a1 y se coloca H5= {V1, V2, V3, V4, V5}
Paso 6: Se elige la arista a16 y se coloca H6= {V1, V2, V3, V4, V5,V6}
V1 V2
V3
a3
V4
a11
a1
a14
V5
V1 V2
V3
a3
V4
a11
a1
a14
V5 V6
a16

9. Paso 7: Se elige la arista a20 y se coloca H7= {V1,V2,V3,V4,V5,V6,V8}
Paso 8: Se elige la arista a18 se coloca H8= {V1, V2, V3, V4, V5,V6, V8,V7}
Obteniendo el árbol generador
V1 V2
V3
a3
V4
a11
a1
a14
V5 V6
a16
V8
a20
V1 V2
V3
a3
V4
a11
a1
a14
V5 V6
a16
V8
a20
a18V7

10. j) Subgrafo parcial
V1
V3
V2
a2
a3
V4
V7
V5
a15
a17
V8
V6
a19
a20
k) Demostrar si es eureliano aplicando algoritmo de Fleury:
No es eureliano debido a que no es posible la construcción de un
ciclo eureliano, ya que no todos los vértices tienen grado par .

11. V1 V2
V3
a3
V4
a2
a17
V7
V6
a15
a20
a10
V8
V5
a19
l) Demostrar si es Hamiltoniano
Si es hamiltoniano porque el ciclo pasa por todos sus vértices

12. Ponderación de las aristas
Aristas a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a1
Ponder. 2 3 4 3 2 3 4 1 4 3 2 2 4
Dado el siguiente Dígrafo:
a) Encontrar Matriz Conexión
b) ¿Es Simple?
c) Encontrar una cadena
elemental no simple de grado 5
d) Encontrar un ciclo simple
e) Demostrar si es fuertemente
conexo utilizando la matriz de
accesibilidad
f) Encontrar la distancia de V2
a los demás vértices utilizando
el algoritmo de Dijkstra

13. a) Matriz de Conexión
a1 a2 a3 a4 a5 a6 a7 a8 a9 a1
0
a1
1
a1
2
a1
3
a1
4
V1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
V2 1 0 0 0 0 0 0 0 0 1 0 0 0 0
V3 0 1 0 0 1 0 0 0 0 0 0 0 0 0
V4 0 0 1 0 0 0 0 1 0 0 1 0 0 0
V5 0 0 0 0 0 1 1 0 0 0 0 0 0 1
V6 0 0 0 1 0 0 0 0 0 0 0 1 0 0
b) ¿Es simple?
El dígrafo es simple ya que no contiene lazos ni aristas
paralelas, solo opuestas

14. c) Encontrar una cadena no simple no elemental.
V5, a11, V4, a12, V6, a14,V5, a11, V4, a9, V1
d) Encontrar un ciclo simple.
V5, a11, V4, a12, V6, a14, V5
e) Demostrar si es fuerte conexo utilizando la matriz de
accesibilidad.
0 1 1 0 1 0
0 0 1 1 0 1
0 0 0 1 1 0
1 0 0 0 0 1
0 1 0 0 0 1
0 0 0 0 1 0
MC=
0 1 1 1 1 1
1 0 0 1 1 0
1 1 1 1 0 1
0 1 1 0 1 0
1 0 1 1 0 1
0 1 0 1 0 1
MC2=

15. 1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 0 1 1
0 1 1 1 1 1
0 1 1 1 1 1
1 0 1 1 0 1
MC3=
1 1 1 1 1 1
1 0 1 1 1 1
0 1 1 1 1 1
1 1 0 1 1 1
1 1 1 1 1 1
1 1 1 1 0 1
MC4=
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 0 1
MC5=

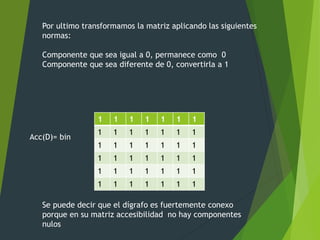
16. Se calcula la matriz aplicando la formula
Acc (Ds)= bin [ In + M + M2 + … + M-1]
En este caso seria
Acc(D)= bin [I6 + M + M2+ M3 + M4 + M5]
Acc(D)= bin
3 4 5 4 5 4
4 2 5 5 5 5
3 4 3 4 4 4
4 4 3 5 4 4
3 4 4 5 4 5
3 3 3 4 1 4

17. Por ultimo transformamos la matriz aplicando las siguientes
normas:
Componente que sea igual a 0, permanece como 0
Componente que sea diferente de 0, convertirla a 1
Acc(D)= bin
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
1 1 1 1 1 1 1
Se puede decir que el dígrafo es fuertemente conexo
porque en su matriz accesibilidad no hay componentes
nulos

18. f) Encontrar la distancia de V2 a los vértices utilizando el Algoritmo
Dijkstra
-Primero se ubica el vértice inicial
- Luego los vértices cercanos al V2 para estudiarlos
-A continuación se agrega etiquetas a los vértices estudiados por ejemplo
[3,1] (1,1)
En donde
[] Símbolo de la iteración en estudio
3 Ponderación de la arista mas lo que la precede
1 Vértice estudiado
(1,1) # de la iteración
- Seguidamente se coloca la ponderación de la arista mas la ponderación
de la etiqueta anterior que está directamente al vértice estudiado
- Se colocará al lado de la etiqueta el numero de iteración que se está
realizando
- Por ultimo se estudian las distancia y se escoge la menor

19. [2,2](1)
[0](0)
[3,2](1) [2,2](1)
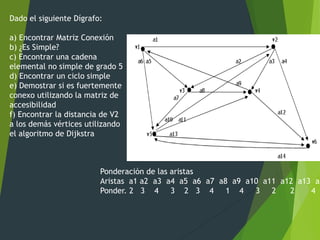
Ponderación de las aristas
Aristas a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
Poder . 2 3 4 3 2 3 4 1 4 3 2 2 4 3
De V2 a V1: 2, de V2 a V2: 3, de V2 a V3: 3, de V2 a V4: 3, de V2 a V5: 4, de V2 a
V6: 3