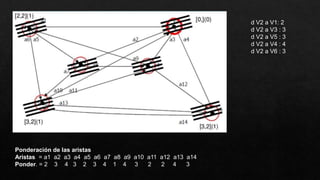
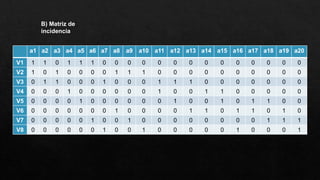
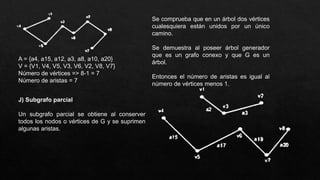
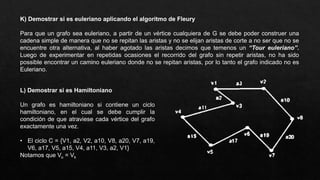
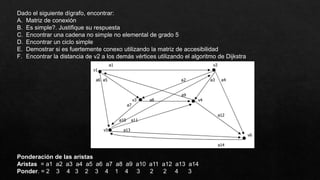
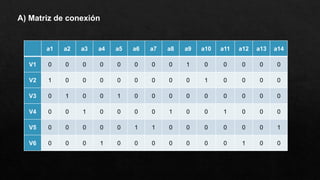
El documento presenta un grafo y solicita realizar diferentes operaciones y análisis sobre él, como encontrar la matriz de adyacencia y de incidencia, determinar si es conexo, simple, regular o completo, encontrar una cadena y un ciclo, construir un árbol generador, un subgrafo parcial, y analizar si es euleriano u hamiltoniano. También se presenta un dígrafo y se pide encontrar su matriz de conexión, una cadena y un ciclo, demostrar si es fuertemente conexo y hallar las distancias desde un vértice aplicando

2. Dado el siguiente grafo, encontrar:
A. Matriz de adyancencia
B. Matriz de incidencia
C. Es conexo?. Justifique su respuesta
D. Es simple?. Justifique su respuesta
E. Es regular?. Justifique su respuesta
F. Es completo? Justifique su respuesta
G. Una cadena simple no elemental de
grado 6
H. Un ciclo no simple de grado 5
I. Arbol generador aplicando el algoritmo
constructor
J. Subgrafo parcial
K. Demostrar si es euleriano aplicando el
algoritmo de Fleury
L. Demostrar si es hamiltoniano

3. V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 1 0 1 0
V2 1 0 1 0 0 1 1 1
V3 1 1 0 1 1 1 0 1
V4 1 0 1 0 1 1 0 0
V5 1 0 1 1 0 1 1 0
V6 0 1 1 1 1 0 1 1
V7 1 1 0 0 1 1 0 1
V8 0 1 1 0 0 1 1 0
A) Matriz de
adyacencia

4. B) Matriz de
incidencia
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15 a16 a17 a18 a19 a20
V1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
V2 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
V3 0 1 1 0 0 0 1 0 0 0 1 1 1 0 0 0 0 0 0 0
V4 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
V5 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 1 0 0
V6 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 1 0 1 0
V7 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
V8 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1

5. C) Es conexo? Justifique su respuesta.
Se dice convexo si para cualquier par de vértices
de “a” y “b” en G existe al menos una trayectoria
de “a” a “b”. Bajo esta definición podemos decir
que sí es conexo, ya que para todo par de
vértices se encuentran conectados o tienen un
camino que los une
D) Es simple? Justifique su respuesta.
Si, es un grafo simple porque cumple la norma
de que ningún vértice tiene lazo, además cada
vértice está unido por una sola arista.
E) Es regular? Justifique su respuesta.
No, ya que hay vértices que tienen grados o
valencias diferentes.
F) Es completo? Justifique su respuesta.
No es completo porque posee aristas paralelas y
más de una arista por cada par de vértices,
dando origen a los sub-grafos.
G) Una cadena simple no elemental de grado
6.
Una cadena simple es una secuencia finita
alternada de vértices y aristas, sin repetir aristas,
no elemental quiere decir que pueden repetirse
los vértices, y por ultimo, el grado nos indica la
cantidad de aristas que debe tener la cadena.
Por ejemplo:
V3 = Grado 6
V6 = Grado 6

6. H) Un ciclo no simple de grado 5
• Ciclo simple: Es el ciclo que a su vez es
una cadena simple.
• Ciclo no simple: Es un ciclo que no es una
cadena simple.
No se puede demostrar, ya que las aristas son
distintas del grafo. No hay cadenas no simples
de ningún grado.
I) Árbol generador aplicando el algoritmo
constructor.
1) Seleccionar un vértice S1, hacer H1={S1}
2) Seleccionamos una arista a1 que tenga un
extremo en H1 y el otro extremo en un
vértice S2 ∉ H2. Hacer H2 U {S3}
3) Seleccionamos una arista a2 que tenga un
extremo en H2 y el otro extremo en un
vértice S3 ∉ H2. Hacer H2 U {S3}
1) Seleccionamos el vértice v1 => H1={V1}
2) Seleccionamos la arista a4 =>
H2={V1,V4}
A15 => H3={V1, V4, V5}
A12 => H4={V1, V4, V5, V3}
A13 => H5={V1, V4, V5, V3, V6}
A8 => H6={V1, V4, V5, V3, V6, V2}
A10 => H7={V1, V4, V5, V3, V6, V2, V8}
A20 => H8={V1, V4, V5, V3, V6, V2, V8, V7}

7. Se comprueba que en un árbol dos vértices
cualesquiera están unidos por un único
camino.
Se demuestra al poseer árbol generador
que es un grafo conexo y que G es un
árbol.
Entonces el número de aristas es igual al
número de vértices menos 1.
A = {a4, a15, a12, a3, a8, a10, a20}
V = {V1, V4, V5, V3, V6, V2, V8, V7}
Número de vértices => 8-1 = 7
Número de aristas = 7
J) Subgrafo parcial
Un subgrafo parcial se obtiene al conserver
todos los nodos o vértices de G y se suprimen
algunas aristas.

8. K) Demostrar si es euleriano aplicando el algoritmo de Fleury
Para que un grafo sea euleriano, a partir de un vértice cualquiera de G se debe poder construer una
cadena simple de manera que no se repitan las aristas y no se elijan aristas de corte a no ser que no se
encuentre otra alternativa, al haber agotado las aristas decimos que temenos un “Tour euleriano”.
Luego de experimentar en repetidas ocasiones el recorrido del grafo sin repetir aristas, no ha sido
possible encontrar un camino euleriano donde no se repitan aristas, por lo tanto el grafo indicado no es
Euleriano.
L) Demostrar si es Hamiltoniano
Un grafo es hamiltoniano si contiene un ciclo
hamiltoniano, en el cual se debe cumplir la
condición de que atraviese cada vértice del grafo
exactamente una vez.
• El ciclo C = {V1, a2, V2, a10, V8, a20, V7, a19,
V6, a17, V5, a15, V4, a11, V3, a2, V1}
Notamos que Vo = Vk

9. Dado el siguiente dígrafo, encontrar:
A. Matriz de conexión
B. Es simple?. Justifique su respuesta
C. Encontrar una cadena no simple no elemental de grado 5
D. Encontrar un ciclo simple
E. Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad
F. Encontrar la distancia de v2 a los demás vértices utilizando el algoritmo de Dijkstra
Ponderación de las aristas
Aristas = a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
Ponder. = 2 3 4 3 2 3 4 1 4 3 2 2 4 3

10. A) Matriz de conexión
a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
V1 0 0 0 0 0 0 0 0 1 0 0 0 0 0
V2 1 0 0 0 0 0 0 0 0 1 0 0 0 0
V3 0 1 0 0 1 0 0 0 0 0 0 0 0 0
V4 0 0 1 0 0 0 0 1 0 0 1 0 0 0
V5 0 0 0 0 0 1 1 0 0 0 0 0 0 1
V6 0 0 0 1 0 0 0 0 0 0 0 1 0 0

11. B) Es simple? Justifique su respuesta.
Se cumple que el dígrafo es simple, ya que no
tiene lazos y no existen arcos paralelos que
partan de un mismo vértice a otro.
C) Encontrar una cadena no simple no
elemental de grado 5.
En las cadenas no simples se pueden repetir los
arcos durante el recorrido y que sea no elemental
también nos permite repetir vértices.
El grado 5 nos indica el número de arcos que
tendrá nuestra cadena.
T = {V4, a9, V1, a5, V3, a8, V4, a9, V1, a6, V5}
D) Encontrar un ciclo simple
El ciclo simple inicia y termina con el mismo
vértice y en ella no se pueden repetir arcos.
C = {V6, a14, V5, a11, V4, a9, V1, a1, V2, a4,
V6}
E) Demostrar si es fuertemente conexo
utilizando la matriz de accesibilidad.
Para comprobar que un grafo es conexo
podemos realizar los siguientes pasos:
1. Hallar la matriz de adyacencia y se Eleva a la
enésima potencia.
2. Se calcula la suma de las potencias de A
hasta An
3. Si todos sus elementos son distintos de cero,
el grafo es conexo,

12. V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 1 0 1
V6 0 0 0 0 1 0
Elevamos la matriz al cuadrado para encontrar
los caminos de tamaño dos (02)
V1 V2 V3 V4 V5 V6
V1 0 0 1 1 1 1
V2 1 0 0 1 1 1
V3 1 1 0 1 0 1
V4 0 1 1 0 1 0
V5 1 0 1 1 1 1
V6 0 1 0 1 0 1
Matriz de adyacencia

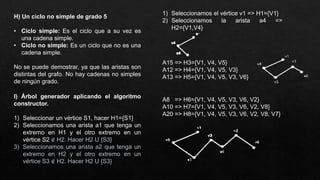
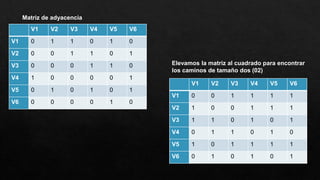
13. Elevamos la matriz a cuatro para encontrar los
caminos de tamaño cuatro (04) M
4
(D)=
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 0 1 1 1 1
V3 0 1 1 1 1 1
V4 1 1 0 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1
Elevamos la matriz a cinco para encontrar los
caminos de tamaño cinco (05) M
5
(D)=
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 0 1 1
V4 0 1 1 1 1 1
V5 0 1 1 1 1 1
V6 1 0 1 1 0 1
Elevamos la matriz al cubo para encontrar los
caminos de tamaño tres (03) M
3
(D)=
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 1 1 1 1 1
V3 1 1 1 1 1 1
V4 1 1 1 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 0 1 1 1 1
V3 0 1 1 1 1 1
V4 1 1 0 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1
Ahora calculamos la matriz de accesibilidad
Acc(D) = bin [I6 + M + M
2
+ M
3
+ M
4
+ M
5
]

14. Luego transformamos la matriz de la siguiente manera:
a) Componente que sea igual a cero(0), permanece como cero
b) Componente diferente de cero (0), se convierte en 1.
V1 V2 V3 V4 V5 V6
V1 1 1 1 1 1 1
V2 1 0 1 1 1 1
V3 0 1 1 1 1 1
V4 1 1 0 1 1 1
V5 1 1 1 1 1 1
V6 1 1 1 1 0 1
Acc(D) = bin
Como la matriz Acc(D) no tiene componentes nulos se dice entonces que el dígrafo es fuertemente conexo.

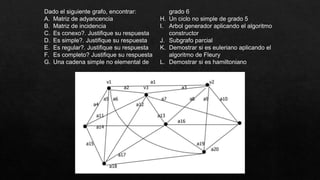
15. F) Encontrar la distancia V2 a los demás verties utilizando el algoritmo DIJKSTRA.
Pasos:
1) Ubicar el vértice de inicio.
2) Ubicar después los vértices más cercanos al V2 para estudiarlo (directamente a él).
3) Agregar etiquetas a cada vértice estudiado:
4) Luego colocar la ponderación de la arista
+ la ponderación de la etiqueta anterior que está
directamente al vértice estudiado.
5) Colocar al lado de la etiqueta el número de iteración
que se está realizando.
6) Luego se estudian las distancias y se ecoge la menor, si hay 2 iguales
se escoge cualquiera.
[3,1]
Símbolo de la iteración
o estudio de distancia
Ponderación de la arista
+ lo que precede
Vértice estudiado
(1,1)# de la
iteración

16. d V2 a V1: 2
d V2 a V3 : 3
d V2 a V5 : 3
d V2 a V4 : 4
d V2 a V6 : 3
Ponderación de las aristas
Aristas = a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14
Ponder. = 2 3 4 3 2 3 4 1 4 3 2 2 4 3