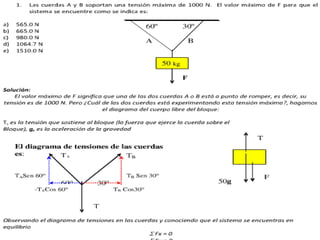
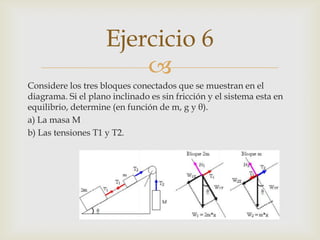
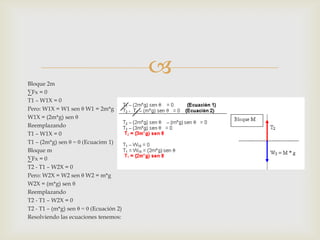
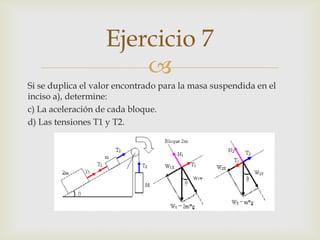
El documento presenta 6 ejercicios de física que involucran conceptos como fuerza, masa, aceleración y movimiento. Los ejercicios resuelven problemas de cálculo de fuerzas, aceleraciones y distancias recorridas usando las leyes de Newton y ecuaciones cinemáticas. El último ejercicio analiza un sistema de bloques conectados en equilibrio e identifica las masas y tensiones involucradas.

1. Por: César Andrés Mora Suárez

2. Ejercicio 1

 Se empuja un ladrillo con una fuerza de 1,2 N y adquiere una
aceleración de 3 m/s2, ¿cuál es la masa del ladrillo?
 Datos:
F = 1,2 N
a = 3 m/s
2
m=?
Solución:

3. Ejercicio 2

 Un camión de 3000 kg de masa, se desplaza con una velocidad
de 100 km/h, y se detiene después de 10 segundos de “clavar”
los frenos. ¿Cuánto vale la fuerza total de rozamiento que hace
posible que se detenga?
Según la segunda Ley: Froz = m . A
Y la fuerza de rozamiento será:
F = 3000 kg . (-2,77 m/seg2) = - 8310N

4. Ejercicio 3

 Un elevador que sube acelerando a razón de 0,5 m/s2 lleva,
apoyada en el piso, una caja que pesa 200 N: ¿Qué fuerzas
actúan sobre la caja? ¿Cuánto valen cada una?
 Para resolver este tipo de problemas, conviene realizar un
diagrama de fuerzas, esto es:

5. 
 Aquí visualizamos las fuerzas que están actuando sobre el
cuerpo: estas son: el peso P (la fuerza con que la tierra lo atrae)
y la fuerza de contacto que el piso del ascensor ejerce sobre el
cuerpo F. De acuerdo con la ecuación de Newton y
considerando positivas a todas las fuerzas que acompañan al
movimiento, en este caso hacia arriba:
F–P=m.a
Despejando:
F=m.a+P
Para calcularlo debemos conocer la masa del cuerpo, su peso y la
aceleración:
P = 200 N

6. 
a = 0,5 m/s2
Sustituyendo estos valores, tenemos:
F = 20,4 kg . 0,5 m/s2+ 200 N = 210, 2 N

7. Ejercicio 4

a) Determinar la aceleración de un cajón de 20 kg a lo largo de un
suelo horizontal cuando se empuja con una fuerza resultante de 10
N paralela al suelo.
b) ¿Hasta dónde se moverá la caja en 5 años (partiendo del
reposo)?
Solución
a)
b) La distancia recorrida viene dada por la Ecuación 1.3

8. Ejercicio 5

Cuando la velocidad es constante, por la primera ley de Newton, la
fuerza resultante debe ser cero. La fuerza en el carro debe ser igual
a la resistencia al movimiento. Así que la fuerza de resistencia de
movimiento es de 1000 N.
b)La fuerza resultante sobre el carro es 1200 - 1000 = 200 N
Por la ecuación 2,2

9. 

10. 

11. Ejercicio 6

Considere los tres bloques conectados que se muestran en el
diagrama. Si el plano inclinado es sin fricción y el sistema esta en
equilibrio, determine (en función de m, g y θ).
a) La masa M
b) Las tensiones T1 y T2.

12. Bloque 2m

∑Fx = 0
T1 – W1X = 0
Pero: W1X = W1 sen θ W1 = 2m*g
W1X = (2m*g) sen θ
Reemplazando
T1 – W1X = 0
T1 – (2m*g) sen θ = 0 (Ecuaciσn 1)
Bloque m
∑Fx = 0
T2 - T1 – W2X = 0
Pero: W2X = W2 sen θ W2 = m*g
W2X = (m*g) sen θ
Reemplazando
T2 - T1 – W2X = 0
T2 - T1 – (m*g) sen θ = 0 (Ecuación 2)
Resolviendo las ecuaciones tenemos:

13. 
Bloque M
∑FY = 0
T2 – W3 = 0
T2 = W3
W3 = M * g
T2 = M * g
Pero: T2 = (3m*g) sen θ
T2 = M * g
M * g = (3m*g) sen θ
a) La masa M
M = 3 m sen θ

14. Ejercicio 7

Si se duplica el valor encontrado para la masa suspendida en el
inciso a), determine:
c) La aceleración de cada bloque.
d) Las tensiones T1 y T2.

15. La masa es M = 3 m sen 9

El problema dice que se duplique la masa
→ M = 2*(3 m sen 9)
M = 6 m sen 9
Al duplicar la masa, el cuerpo se desplaza hacia la derecha.
Bloque 2m
ΣFx = 2m * a
T1 – W1X = 2m * a
Pero: W1X = W1 sen 9 W1 = 2m*g
W1X = (2m*g) sen 9
Reemplazando
T1 – W1X = 0
T1 – (2m*g) sen 9 = 2m * a (EcuaciGn 1)

16. 
Bloque m
ΣFx = m * a
T2 - T1 – W2X = m * a
Pero: W2X = W2 sen 9 W2 = m*g
W2X = (m*g) sen 9
Reemplazando
T2 - T1 – W2X = m * a
T2 - T1 – (m*g) sen 9 = m *a (Ecuación 2)
Bloque M
ΣFY = 6 m sen 9 * a
W3 - T2 = 6 m sen 9 * a
W3 = 6 m sen 9 * g
6 m sen 9 * g - T2 = 6 m sen 9 * a (Ecuación 3)

17. 

18. 
Despejando la ecuación 3 para hallar T26 m sen 9 * g -
T2 = 6 m sen 9 * a (Ecuación 3)6 m sen 9 * g - 6 m sen 9 *
a = T26 m sen 9 ( g - a ) = T2
Despejando la ecuación 1 para hallar T1
T1 – (2m*g) sen 9 = 2m * a (EcuaciGn 1)
T1 = 2m * a + 2m*g sen 9

19. 

20. 
a. Por la acción de la segunda ley de newton, tenemos:
a1 = 3 m/seg2
a2 =1 m/seg2
F = m1 * a1 (Ecuación 1)
F = m2 * a2 (Ecuación 2)