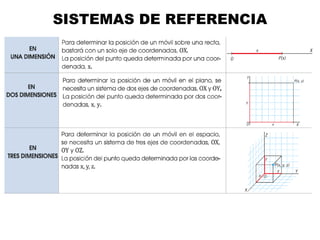
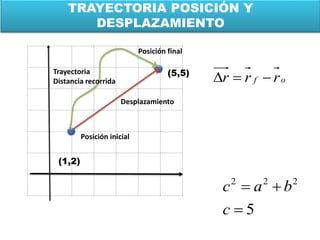
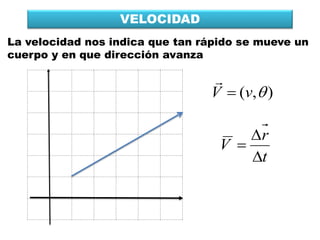
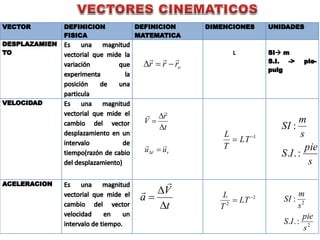
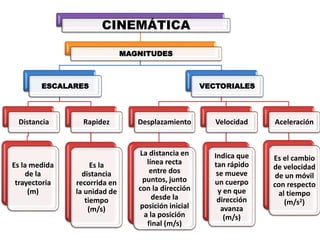
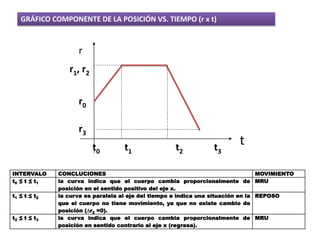
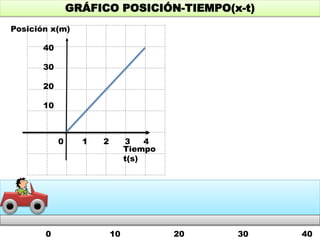
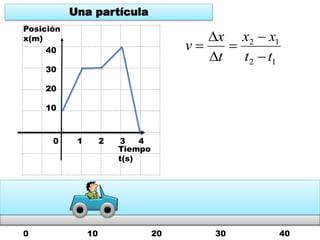
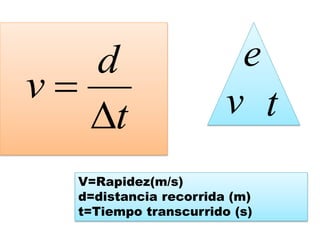
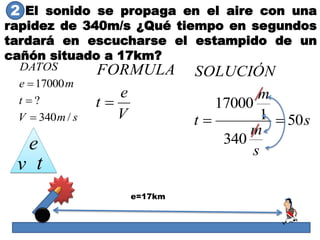
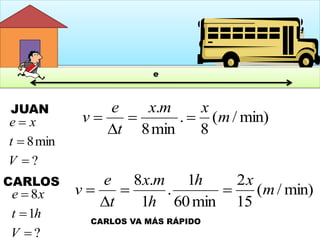
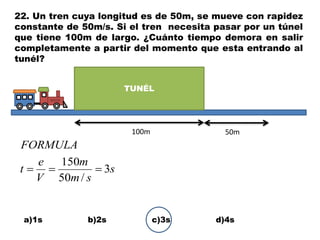
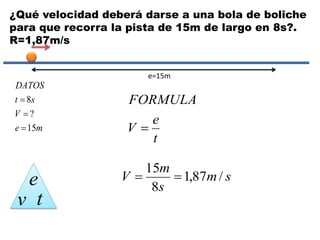
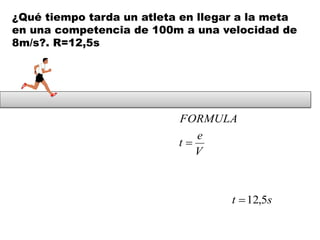
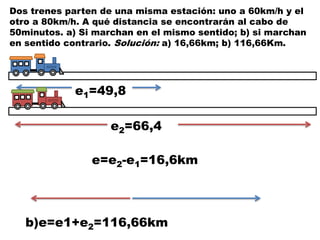
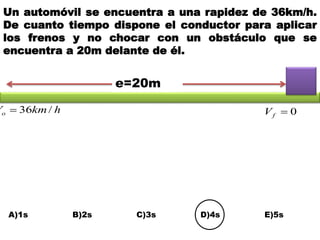
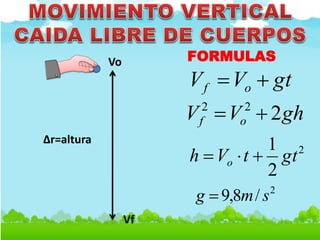
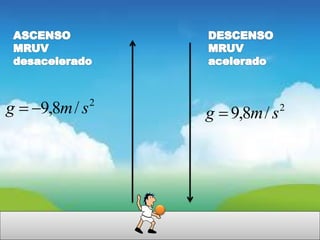
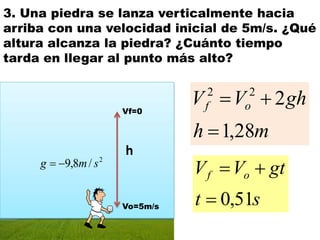
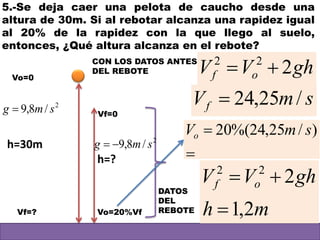
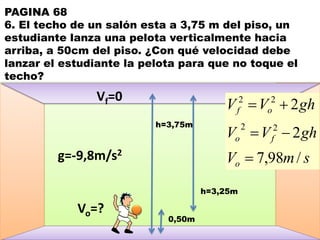
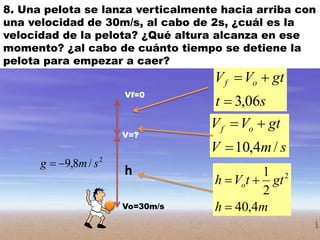
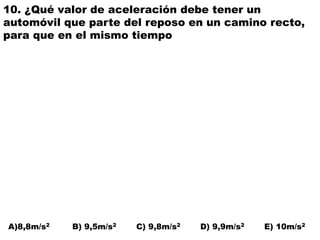
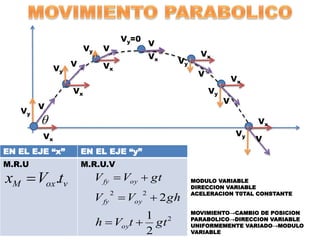
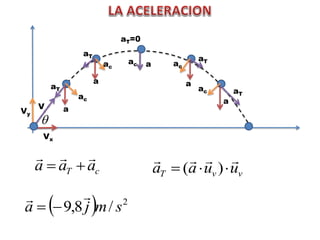
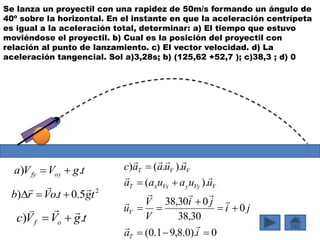
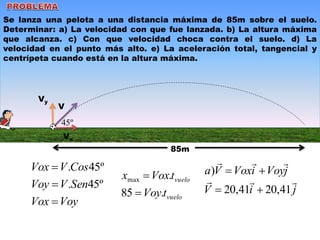
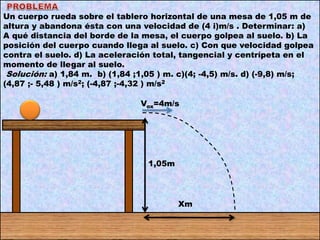
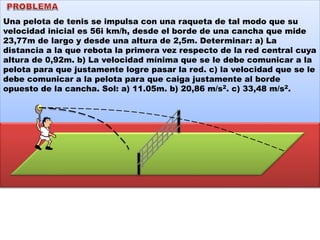
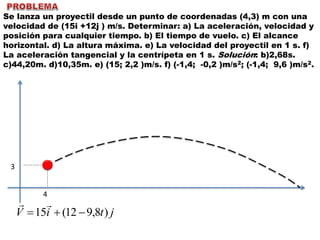
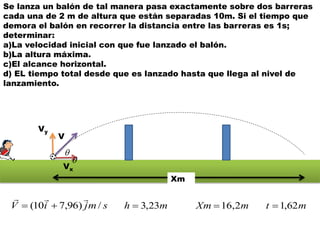
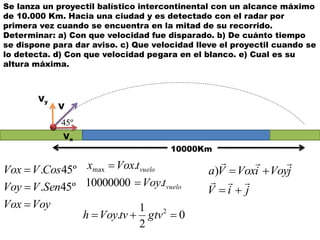
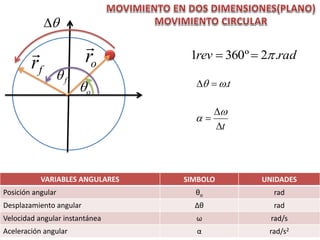
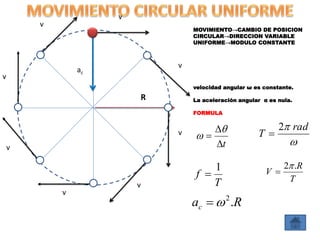
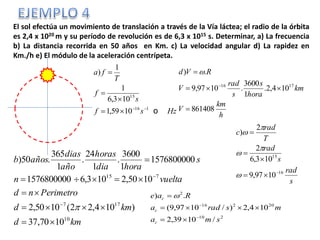
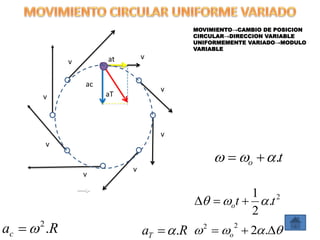
Este documento contiene definiciones y conceptos relacionados con la cinemática, incluyendo movimiento rectilíneo uniforme, velocidad, aceleración, gráficos de posición-tiempo y velocidad-tiempo, y ejemplos de problemas cinemáticos con sus respectivas soluciones. Se definen magnitudes escalares como distancia y rapidez, y vectoriales como desplazamiento y velocidad. También se explican conceptos como trayectoria, reposo y movimiento.

1. BLOQUE
1
drvictorcaiza@hotmail.com
Contenido

2. SISTEMAS DE REFERENCIA

3. MOVIMIENTO RECTILINEO UNIFORME
MOVIMIENTO RECTILINEO UNIFORME VARIADO
MOVIMIENTO CIRCULAR UNIFORME
MOVIMIENTO CIRCULAR UNIFORME VARIADO
MOVIMIENTO VERTICAL
MENU PRINCIPALdrvictorcaiza@hotmail.com
DEFINICIONES
MOVIMIENTO PARABOLICO

4. REPOSO
MOVIMIENTO
TRAYECTORIA
DISTANCIA Y DESPLAZAMIENTO
RAPIDEZ Y VELOCIDAD
ACELERACIÓN
TIEMPO

5. TRAYECTORIA POSICIÓN Y
DESPLAZAMIENTO
Posición inicial
Posición final
Trayectoria
Distancia recorrida
Desplazamiento
of rrr 
(1,2)
(5,5)
5
222


c
bac

6. VELOCIDAD
La velocidad nos indica que tan rápido se mueve un
cuerpo y en que dirección avanza
),( vV 

t
r
V




7. orrr


vr uu
t
r
V


 




1
 LT
T
L
s
pie
IS
s
m
SI
:..
:
t
V
a




 2
2

 LT
T
L
2
2
:..
:
s
pie
IS
s
m
SI

8. CINEMÁTICA
MAGNITUDES
ESCALARES
Distancia
Es la medida
de la
trayectoria
(m)
Rapidez
Es la
distancia
recorrida en
la unidad de
tiempo
(m/s)
VECTORIALES
Desplazamiento
La distancia en
línea recta
entre dos
puntos, junto
con la dirección
desde la
posición inicial
a la posición
final (m/s)
Velocidad
Indica que
tan rápido
se mueve
un cuerpo
y en que
dirección
avanza
(m/s)
Aceleración
Es el cambio
de velocidad
de un móvil
con respecto
al tiempo
(m/s2)

10. MOVIMIENTO→CAMBIO DE POSICION
RECTILINEO→DIRECCION CONSTANTE
UNIFORME→MODULO DE LA VELOCIDAD CONSTANTE
x1 x2
t
r
V





jVyVxiV


t
r
V




12. GRÁFICO COMPONENTE DE LA POSICIÓN VS. TIEMPO (r x t)
t
r
t0 t1 t2 t3
r1, r2
r0
r3
INTERVALO CONCLUCIONES MOVIMIENTO
t0 ≤ t ≤ t1 la curva indica que el cuerpo cambia proporcionalmente de
posición en el sentido positivo del eje x.
MRU
t1 ≤ t ≤ t2 la curva es paralela al eje del tiempo e indica una situación en la
que el cuerpo no tiene movimiento, ya que no existe cambio de
posición (∆r2 =0).
REPOSO
t2 ≤ t ≤ t3 la curva indica que el cuerpo cambia proporcionalmente de
posición en sentido contrario al eje x (regresa).
MRU

13. GRÁFICO COMPONENTE DE LA RAPIDEZ VS. TIEMPO (V x t)
V1=K
V2=K
V3=K
t0 t1 t2 t3
V
t
INTERVALO CONCLUSIONES Distancia Movimiento
t0 ≤ t ≤ t1 la curva indica que el cuerpo tiene una rapidez
constante, positiva, por lo que se mueve en el
sentido positivo del eje x.
∆r1 = V1 (t1 –t0) MRU
t1 ≤ t ≤ t2 la curva indica que el cuerpo tiene rapidez nula, lo
que significa que no tiene movimiento.
∆r2= 0 REPOSO
t2 ≤ t ≤ t3 la curva indica que el cuerpo tiene una rapidez
constante, negativa.
∆r3 = -V3(t3 - t2) MRU

14. 0 1 2 3 4
Tiempo
t(s)
Posición x(m)
GRÁFICO POSICIÓN-TIEMPO(x-t)
40
30
20
10
0 10 20 30 40

15. 0 1 2 3 4
Tiempo
t(s)
Posición
x(m)
Una partícula
40
30
20
10
12
12
tt
xx
t
x
v






0 10 20 30 40

16. t
d
v


V=Rapidez(m/s)
d=distancia recorrida (m)
t=Tiempo transcurrido (s)
e
v t

17. Un ciclista se mueve con m.r.u. a razón de
5m/s ¿Qué distancia en kilómetros podrá
recorrer en un cuarto de hora?
DATOS
V=5m/s
t=15min
e=?
tve .
km
m
km
me
ms
s
m
e
5,4
1000
1
.4500
4500900.5


e
v t
s
s
900
min1
60

1

18. El sonido se propaga en el aire con una
rapidez de 340m/s ¿Qué tiempo en segundos
tardará en escucharse el estampido de un
cañón situado a 17km?
smV
t
me
DATOS
/340
?
17000



V
e
t
FORMULA

s
s
m
m
t
SOLUCIÓN
50
340
1
17000

e=17km
e
v t
2

19. Una partícula se desplaza −𝟗 𝒊 + 𝟏𝟐 𝒋 𝒌𝒎,con la
velocidad constante, durante 36min. Determinar:
a)La velocidad en Km./h.
b)La rapidez en m/s.
c)El vector unitario de la velocidad,
d)El vector unitario del desplazamiento.
ji
hKm
hKmji
u
V
V
uc
V
V





8,06,0
/25
/)2015(
)




s
m
V
s
h
km
m
h
km
V
Vb
94,6
3600
1
.
1
1000
.25
)20()15() 22



h
km
jiV
h
Kmji
V
t
r
Va
)2015(
6,0
)129(
)











ji
Km
Kmji
u
r
r
ud
r
r





8,06,0
15
)129(
)








h
h
6,0
min60
1

3
DATOS
.∆𝑟 = −9 𝑖 + 12 𝑗 𝑘𝑚
t=36min

20. Un móvil se mueve con la velocidad constante de
𝟏𝟓 𝒊 + 𝟏𝟖 𝒋 𝒎/𝒔 durante 2 min. Determinar: a) El
desplazamiento realizado, b) La distancia recorrida,
c) El vector unitario de la velocidad, d) El vector
unitario del desplazamiento.
mjir
s
s
m
jir
tVra
)21601800(
120.)1815(
.)






m
rb
69,2811
21601800) 22


jiu
m
mji
u
r
r
ud
jiu
sm
smji
u
V
V
uc
r
r
r
V
V
V










768,0640,0
69,2811
)21601800(
)
768,0640,0
/43,23
/)1815(
)













4

21. Una partícula se mueve desde el punto
A(30,40)cm al punto B(-80,50)cm en 5
segundos. Determinar
a) El desplazamiento en metros.
b) la distancia recorrida en metros.
c) La velocidad en m/s
d) La rapidez en m/s
mjir
cm
m
cmjir
jijir
rrra of
)1,01,1(
100
1
.)10110(
)4030()5080(
)








smVd
smji
ji
t
r
Vc
/22,0)
/)02,022,0(
5
1,01,1
)










5
mrb 1,11,0)1,1() 22


22. EJERCICIOS
DE REPASO

23. Un trueno se ha oído 1 minuto y 18segundos
después de verse el relámpago. ¿A qué
distancia se ha producido el fenómeno?
(velocidad del sonido= 340m/s)
?
/340
18min1



e
smV
segutot
DATOS
tve .
ms
s
m
e 2652078.340 

24. Un automóvil tarda en recorrer 2,5Km en
3minutos y 30 segundos. ¿Cuál es la
velocidad en m/s del automóvil?
Kme
V
ssegutot
DATOS
5,2
?
21030min3



t
e
V
FORMULA

sm
s
m
V /9,11
210
2500

m
km
m
2500
1
1000


25. Un corredor avanza a razón de 5m/s. ¿Qué
distancia recorrerá en 15minutos?.
e
t
e
v


ms
s
m
tve 4500900.5. 
DATOS
v=5m/s
t=15min
e=?
s
s
900
min1
60


26. min)/(
8
.
min8
.
m
xmx
t
e
v 


JUAN
CARLOS
min)/(
15
2
min60
1
.
1
.8
m
xh
h
mx
t
e
v 


CARLOS VA MÁS RÁPIDO
e
?
min8



V
t
xe
?
1
8



V
ht
xe

27. LIBRO PAG 59
19. ¿Qué distancia en Km recorre un auto que
viaja con rapidez constante de 72km/h durante 20
minutos?
?
/72
min20



e
hkmV
t
DATOS
tve .h
h
3
1
min60
1

kmh
h
km
e 24
3
1
.72 

28. 20. ¿Qué rapidez en km/h constante debe llevar
un auto que recorre 12km en media hora?
kme
V
ht
DATOS
12
?
5,0



t
e
V
FORMULA

hkm
h
km
V /24
5,0
12


29. 21. ¿Cuánto tarda un auto en recorrer 150km a
una rapidez promedio de 20m/s?
Respuesta 2h 5min
kme
smV
t
DATOS
150
/20
?



V
e
t
FORMULA

s
s
m
m
t
SOLUCIÓN
7500
20
1
150000

h
s
h
s 0833,2
3600
1
.7500 
min599,4
1
min60
.0833,0
2

h
h
h

30. 22. Un tren cuya longitud es de 50m, se mueve con rapidez
constante de 50m/s. Si el tren necesita pasar por un túnel
que tiene 100m de largo. ¿Cuánto tiempo demora en salir
completamente a partir del momento que esta entrando al
tunél?
a)1s b)2s c)3s d)4s
TUNÉL
100m 50m
s
sm
m
V
e
t
FORMULA
3
/50
150


31. Un automóvil recorre 50km ¿Con que rapidez
recorrió durante 1hora? R=13,89m/s.
kme
V
s
h
s
ht
DATOS
50
?
3600
1
3600
.1



t
e
V
FORMULA

e=50km
sm
s
m
V /89,13
3600
50000


32. ¿Qué velocidad deberá darse a una bola de boliche
para que recorra la pista de 15m de largo en 8s?.
R=1,87m/s
me
V
st
DATOS
15
?
8



e
v t
e=15m
t
e
V
FORMULA

sm
s
m
V /87,1
8
15


33. ¿Qué tiempo tarda un atleta en llegar a la meta
en una competencia de 100m a una velocidad de
8m/s?. R=12,5s
V
e
t
FORMULA

st 5,12

34. Dos puntos A y B están separados por una distancia de 500 m.
Desde A parte un móvil que tarda 25 segundos en llegar a B.
Simultáneamente y desde B parte otro móvil que tarda 10
segundos en llegar a A. Si las trayectorias son rectilíneas,
hallar analítica y gráficamente dónde y cuánto se encuentran.
A
B
A B500m
me
st
me
st
B
B
A
A
500
10
500
25




sm
s
m
V
sm
s
m
V
t
r
V
B
A
A
/50
10
500
/20
25
500





x 500-x
tA
tB
mx
x
xx
xx
xx
xx
V
e
V
e
tt
B
B
A
A
BA
86,142
70
10000
1000070
100002050
201000050
)500(2050
50
500
20
eencontrarshasta









st
sm
m
t
V
e
t
A
A
A
A
A
14,7
/20
86,142




35. Dos trenes parten de una misma estación: uno a 60km/h y el
otro a 80km/h. A qué distancia se encontrarán al cabo de
50minutos. a) Si marchan en el mismo sentido; b) si marchan
en sentido contrario. Solución: a) 16,66km; b) 116,66Km.
e1=49,8
e2=66,4
e=e2-e1=16,6km
b)e=e1+e2=116,66km

37. La velocidad es variable
La aceleración es constante
MOVIMIENTO→CAMBIO DE POSICION
RECTILINEO→DIRECCION CONSTANTE
U. VARIADO→MODULO V CAMBIA UNIFORMEMENTE
aeVV of 222

2
2
1
attVe o 
atVV of 

38. aeVV of 222

2
2
1
attVe o 
atVV of 
FORMULAS DEL MOVIMIENTO RECTILINEO
UNIFORME VARIADO
REPETIR 1000 VECES CADA UNA=3000

39. Un móvil arranca y después de 5 min. De moverse
por una trayectoria recta, adquiere una rapidez de
80Km./h. Determinar: a) La aceleración producida.
b) La rapidez media. c) La distancia recorrida.
ec
Vb
aa
hkmV
st
V
DATOS
m
f
o
)
)
)
/80
300min5
0





2
/074,0
300
/22,22
)
sma
s
sm
a
t
VV
a
atVVa
of
of





smV
VV
Vb
m
of
m
/11,11
2
)



mssmse
attVec o
3330)300)(/074,0)(5,0()300)(0(
2
1
.)
22
2


0oV

40. Un móvil que va por una carretera recta con una
rapidez de 5m/s, es acelerado durante 10s, tiempo en
el que realiza un recorrido de 100m. Determinar la
rapidez final en m/s.




f
o
V
me
st
smV
DATOS
100
10
/5
atVV
FORMULA
of 
2
2
1
attVe o 
A)10 B)15 C)20 D)25 E)30
smVo /5 ?fV
e=100m
MRUA

41. Un objeto parte del reposo aumenta su
rapidez a razón de 2,5 m/s por cada segundo
que transcurre. a) ¿Cuál es su aceleración?
b) ¿Cuál es su rapidez en 20s?
?)
/5,2V
1st
0V
DATOS
f
o




aa
sm
atVV
FORMULA
of 
2
/5,2 sma
t
VV
a of







a
?V
20st
0V
DATOS
f
o atVV
FORMULA
of 
smVf /50

42. 24) El conductor de un automóvil que se
mueve a 72km/h aplica los frenos y se
detiene con aceleración constante después
de 4s. ¿Qué distancia recorrió mientras se
detuvo?
hkmVo /72 0fV
?
0
4
/20




e
V
st
smV
DATOS
f
o atVV
FORMULA
of 
2
/5 sma
t
VV
a of



M.R.U.Desacelerado
me
attVe o
40
2
1 2



43. Un móvil arranca y después de 5 min. De moverse
por una trayectoria recta, adquiere una velocidad de
𝟒𝟎 𝒊 − 𝟔𝟎 𝒋 Km./h. Determinar: a) La aceleración
producida en m/s2). b) La velocidad media en m/s. c)
La rapidez media en m/s. d) El desplazamiento
realizado en m. e) La distancia recorrida en m.
re
rd
Vc
Vb
aa
hkjiV
st
V
DATOS
m
m
f
o





)
)
)
)
)
/)6040(
300min5
0





2
/)056,0037,0(
300
/)67,1611,11(
)
smjia
s
smji
a
t
VV
a
tavva
of
of












smjiV
s
h
km
m
h
km
jiV
f
f
/)67,1611,11(
3600
1
.
1
1000
.)6040(




smjiV
smji
V
VV
Vb
m
m
of
m
/)84,856,5(
2
/)67,1611,11(
2
)










smV
Vc
m
m
/02,10
)34,8(56,5) 22


mjir
jir
tatVrd o
)25201665(
)300)(056,0037,0(
2
1
2
1
)
2
2






mr
re
37,3020
)2520(1665) 22



44. La velocidad de un móvil animado de movimiento rectilíneo uniforme acelerado, pasa de
(12; 9) m/s. a (30; -15)m/s. por la acción de una aceleración de módulo 0,6 m / s2.
Determinar: a) El tiempo empleado. b) La velocidad media. c) La rapidez media. d) El
desplazamiento realizado. e) La distancia recorrida. Solucion: a)30,9s. b)21;-3 m/s.
c)24,27m/s d)
re
rd
Vc
Vb
ta
jia
sma
sma
smjiV
smV
smjiV
DATOS
m
m
f
o
o









)
)
)
)
)
)36,048,0(
)º87,36;/6,0(
/6,0
/)1530(
)º87,36;/15(
/)912(
2
2







st
t
a
VV
t
atVVa
of
of
9,30
6,0
1554,33
)






smjiV
ji
V
jiji
V
VV
Vb
m
m
m
of
m
/)321(
2
)642(
2
)912()1530(
2
)













mre
mjir
jijir
jijir
tatVrd o
750)
)450600(
)87,17115,229()1,2788,370(
)9,30)(36,048,0(
2
1
)9,30)(912(
2
1
)
2
2










45. 2
/)19,616,5(
5,3
/)67,2106,18(
)
smjia
s
smji
a
t
VV
aa of










2. Cuando se aplican los frenos de un auto animado de movimiento
rectilíneo, su velocidad es de (-65; -78 ) Km./h. Si el auto se detiene 3,5
s. Determinar: a) La aceleración producida por los frenos. b) El
desplazamiento realizado. c) La distancia recorrida. d) La velocidad
media. e) La rapidez media.
)94,376,31(
)5,3)(19,616,5(
2
1
)5,3)(67,2106,18(
2
1
.)
2
2
jir
jijir
tatVrb o






mc 38,49)
smjimVd /)84,1003,9()


smVmd /11,14) 

46. 2
/43,11
5,3
/400
)
sma
s
sm
a
t
VV
aa of






Cuando se aplican los frenos de un auto animado de
movimiento rectilíneo, su velocidad es de 40m/s. Si
el auto se detiene 3,5 s. Determinar: a) La
aceleración producida por los frenos. b) La distancia
recorrida. c) La rapidez media.
me
r
attVeb o
99,69
)5,3)(43,11(
2
1
)5,3)(40(
2
1
.)
2
2




?)
0V
3,5st
40m/sV
DATOS
f
o




aa
smVo /40 0fV
smc /20)

47. Un automóvil se encuentra a una rapidez de 36km/h.
De cuanto tiempo dispone el conductor para aplicar
los frenos y no chocar con un obstáculo que se
encuentra a 20m delante de él.
hkmVo /36 0fV
e=20m
A)1s B)2s C)3s D)4s E)5s

48. Un automóvil aplica los frenos con una
desaceleración de 5m/s2, cuando su
velocidad es de 50m/s. tiempo en el
que recorre 10m. Determinar la rapidez
final alcanzada.
?V
/5
10e
50m/sV
DATOS
f
2
o




sma
m
A)45,01m/s B)46,24m/s C)48,99m/s D)50,01m/s E)51,25m/s
smVo /5 ?fV
e=10m

50. FORMULAS
Δr=altura
Vo
Vf
gtVV of 
ghVV of 222

2
2
1
gttVh o 
2
/8,9 smg 

51. 2
/8,9 smg  2
/8,9 smg 

52. st
sm
m
t
g
h
t
gth
gttVha o
02.2
/8.9
202
.2
2
1
0
2
1
)
2
2
2






h
DATOS
Vo=0
g=9,8m/s2
h=20m
a) t=?
b) Vf=?
Desde 20 m. de altura se deja caer libremente una
persona al rio. Determinar: a) Qué tiempo tardará en
llegar al agua. b) Con qué velocidad choca contra el
agua.
smV
V
gtVVb
f
f
of
/)80,19(
)02,2)(8.9(0
)





Vo=0

53. 2- Una piedra se deja caer y tarda en
llegar al suelo 5s. ¿Desde que altura se
soltó?
mh
h
gttVh o
5,122
)5)(8.9(
2
1
0
2
1
2
2



DATOS
Vo=0
t=5s
g=9,8m/s2
a)

54. Desde 50 m. de altura se lanza hacia arriba un objeto con una
velocidad de 20m/s. Determinar. a) La altura alcanzada. b)
Cuánto tarda en llegar al suelo. c) Con qué rapidez llega al
suelo. R= a)70,41m. b)5,83s c)37,14m/s
h=50m
Vo=20m/s
Vf=0
h=20,41m
Tiempo de subida
Vo=20m/s
g=-9,8m/s2
Vf=0
t=
Tiempo de bajada
Vo=0
g=9,8m/s2
h=70,41m
t=
st
gtVV of
04,2

st
gth
gttVh o
79,3
2
1
2
1
2
2



smV
gtVVc
f
of
/14,37)79,3(8,90
)



55. 3. Una piedra se lanza verticalmente hacia
arriba con una velocidad inicial de 5m/s. ¿Qué
altura alcanza la piedra? ¿Cuánto tiempo
tarda en llegar al punto más alto?
Vo=5m/s
Vf=0
h2
/8,9 smg 
mh
ghVV of
28,1
222


st
gtVV of
51,0


56. 4.- Una piedra se deja caer sobre un pozo con
agua y a los 2 segundos se escucha el
impacto de la piedra sobre el agua. ¿Cuál es
la profundidad del pozo?
mh 6,19
DATOS
Vo=0
t=2s
g=9,8m/s2
h=?
2
2
1
gttVh o 

57. 5.-Se deja caer una pelota de caucho desde una
altura de 30m. Si al rebotar alcanza una rapidez igual
al 20% de la rapidez con la que llego al suelo,
entonces, ¿Qué altura alcanza en el rebote?
Vo=0
2
/8,9 smg 
Vf=?
h=30m
Vo=20%Vf
h=?
ghVV of 222

Vf=0
DATOS
DEL
REBOTE
smVf /25,24

 )/25,24%(20 smVo
mh
ghVV of
2,1
222


2
/8,9 smg 
CON LOS DATOS ANTES
DEL REBOTE

58. PAGINA 68
6. El techo de un salón esta a 3,75 m del piso, un
estudiante lanza una pelota verticalmente hacia
arriba, a 50cm del piso. ¿Con qué velocidad debe
lanzar el estudiante la pelota para que no toque el
techo?
h=3,75m
Vf=0
Vo=?
0,50m
g=-9,8m/s2
smV
ghVV
ghVV
o
fo
of
/98,7
2
2
22
22



h=3,25m

59. 7. Una piedra se deja caer desde una altura de de
80m y 2 segundos mas tarde

60. 8. Una pelota se lanza verticalmente hacia arriba con
una velocidad de 30m/s, al cabo de 2s, ¿cuál es la
velocidad de la pelota? ¿Qué altura alcanza en ese
momento? ¿al cabo de cuánto tiempo se detiene la
pelota para empezar a caer?
Vo=30m/s
V=?
h
2
/8,9 smg 
Vf=0
smV
gtVV of
/4,10

mh
gttVh o
4,40
2
1 2


st
gtVV of
06,3


61. 9. Si se lanza la pelota del ejercicio anterior
en la luna ¿Cuál es la diferencia de altura
alcanzada con relación a la
Tierra?(g=1,67m/s2)
DATOS TIERRA
Vo=30m/s
Vf=0
g=-9,8m/s2
h=?
mh 46,269mh 92,45
DATOS LUNA
Vo=30m/s
Vf=0
g=-1,67m/s2
h=?
mhhh TIERRALUNA 55,223
ghVV of 222


62. 10. ¿Qué valor de aceleración debe tener un
automóvil que parte del reposo en un camino recto,
para que en el mismo tiempo
A)8,8m/s2 B) 9,5m/s2 C) 9,8m/s2 D) 9,9m/s2 E) 10m/s2

63. 11. Un niño lanza una piedra verticalmente,
0,6segundos después la recibe nuevamente. ¿Qué
altura alcanzó la piedra? ¿Con que velocidad lanzó el
niño la piedra?
DATOS T
t=0,6s
Vf=0
g=-9,8m/s2
h=?
Vo=?h=?
Vf=0
Vo=?
2
/8,9 smg 
t=0,3s
smV
gtVV
o
of
/94,2

mh
ghVV of
44,0
222



64. 12. Una persona que se encuentra en lo alto de un
edificio lanza una pelota verticalmente hacia abajo
con una velocidad de 30m/s, si la pelota llega llega a
la base del edificio en 12 segundos. ¿Cuál es la
altura del edificio?
DATOS T
t=12s
g=9,8m/s2
h=?
Vo=30m/s
mh
h
gttVh o
6,1065
)12)(8,9(5,0)12(30
2
1
2
2




65. Una persona lanza hacia arriba un objeto con una
rapidez inicial de 10m/s. Determinar: a) Qué tiempo
tardará en regresar a su mano. b) Con qué
velocidad choca contra la mano. c) La altura
máxima que alcanza el objeto.DATOS
Vo=10m/s
Vf=0
g=-9.8m/s2
smV
ssmV
gtVVb
f
f
of
/10
)02,1)(/8.9(0
)
2





mr
r
gttVrc o
10,5
)02,1)(8,9(
2
1
)02,1(10
2
1
)
2
2



stt
st
t
g
VV
t
tgVVa
stotal
s
of
of
04,2.2
02.1
8.9
100
.)









66. Un cuerpo es lanzado en un acantilado con una velocidad de (-
26 j) m/s y llega al fondo en 5 s. Determinar: a) Con qué
velocidad llega al fondo. b) La altura del acantilado. c) El
desplazamiento realizado. d) Qué velocidad lleva cuando ha
descendido 15 m. e) El espacio recorrido cuando lleva una
velocidad de (-30j )m /s.
smjV
jjV
tgVVa
f
f
of
/)75(
)5)(8.9()26(
)






mr
rb
5.252
)5)(8.9(
2
1
)5)(26() 2


h
mjr
jjr
tgtVrc o
)5,252(
)5)(8.9(
2
1
)26(
2
1
)
2
2






smjV
smV
V
rgVVd
f
f
f
of
/)14,31(
/14,31
)15)(8.9(2)26(
2)
22
22





mr
g
VV
r
rgVVd
of
of
43,11
)8,9(2
)26()30(
2
2)
22
22
22







68. MODULO VARIABLE
DIRECCION VARIABLE
ACELERACION T0TAL CONSTANTE
MOVIMIENTO→CAMBIO DE POSICION
PARABOLICO→DIRECCION VARIABLE
UNIFORMEMENTE VARIADO→MODULO
VARIABLE
Vx
Vy
V
Vy
V
Vx
Vy V
Vx
Vy=0
V
Vx Vy
V
Vx
Vy
V
Vx
Vy
V
Vx
EN EL EJE “x” EN EL EJE “y”
M.R.U M.R.U.V
voxM tVx .
2
22
2
1
2
gttVh
ghVV
gtVV
oy
oyfy
oyfy




69. Vx
Vy
V
ac
aT
a
ac
aT
a
aT=0
ac a ac
a
aT
ac
a
aT

cT aaa

 vvT uuaa

 )(
  2
/8,9 smja



70. Se dispara un proyectil con una velocidad de 120m/s. y un ángulo de 30º sobre la
horizontal. Determinar: a) La distancia recorrida horizontal y verticalmente a los
5s. b) La altura máxima alcanzada e) El tiempo total de vuelo; f) El alcance
máximo alcanzado del proyectil. R=a)x=177,5m; y=183,67m; b)6,12; c)1271,98m
0
smSenVoy
smCocVox
/60º30.120
/92,103º30.120







y
gttVy
mx
ssmx
tVxa
oy
x
2
0
5,0.
85,519
)5(/97,103
.)
smjiV
jjiV
tgoVVb
/)48,794,35(
)2).(8,9()08,2794,35(
.)






mx
x
tVx vueloox
39,198
)52,5(94,35
.
max
max
max




71. Se lanza un cuerpo con una rapidez de 45 m/s y un ángulo de 37° sobre
la horizontal. Determinar: a) La posición del proyectil en 1 s y 4 s b) La
velocidad del cuerpo a los 2 s y 5 s de lanzamiento. C) La altura
máxima y el alcance horizontal.
0
smSenVoy
smCocVox
/08,27º37.45
/94,35º37.45


mjir
jjir
tgtoVra
)18,2294,35(
)1).(8,9(5,0)1).(08,2794,35(
.5.0.)
2
2






smjiV
jjiV
tgoVVb
/)48,794,35(
)2).(8,9()08,2794,35(
.)






s
g
V
t
tgV
tgVVc
oy
oy
oyfy
76,2
8,9
08,27
.0
.)








mh
h
tgtVh oy
41,37
)76,2)(8,9(5,0)76,2(08,27
.5,0.
max
2
max
2
max



mx
x
tVx vueloox
39,198
)52,5(94,35
.
max
max
max




72. Se lanza un proyectil con una rapidez de 50m/s formando un ángulo de
40º sobre la horizontal. En el instante en que la aceleración centrípeta
es igual a la aceleración total, determinar: a) El tiempo que estuvo
moviéndose el proyectil. b) Cual es la posición del proyectil con
relación al punto de lanzamiento. c) El vector velocidad. d) La
aceleración tangencial. Sol a)3,28s; b) (125,62 +52,7 ); c)38,3 ; d) 0
tgVVa oyfy .) 
2
5.0.) tgtoVrb


tgVVc of .)


0).0.8,91.0(
0
30,38
030,38
).(
)..()






ia
ji
ji
V
V
u
uuauaa
uuaac
T
V
VVyyVxxT
VVT







73. Se lanza una pelota a una distancia máxima de 85m sobre el suelo.
Determinar: a) La velocidad con que fue lanzada. b) La altura máxima
que alcanza. c) Con que velocidad choca contra el suelo. d) La
velocidad en el punto más alto. e) La aceleración total, tangencial y
centrípeta cuando está en la altura máxima.
85m
VoyVox
SenVVoy
CosVVox



º45.
º45.
vuelo
vuelo
tVoy
tVoxx
.85
.max


Vx
Vy
V
º45
jiV
jVoyiVoxVa


41,2041,20
)



74. Un cuerpo rueda sobre el tablero horizontal de una mesa de 1,05 m de
altura y abandona ésta con una velocidad de (4 i)m/s . Determinar: a)
A qué distancia del borde de la mesa, el cuerpo golpea al suelo. b) La
posición del cuerpo cuando llega al suelo. c) Con que velocidad golpea
contra el suelo. d) La aceleración total, tangencial y centrípeta en el
momento de llegar al suelo.
Solución: a) 1,84 m. b) (1,84 ;1,05 ) m. c)(4; -4,5) m/s. d) (-9,8) m/s;
(4,87 ;- 5,48 ) m/s2; (-4,87 ;-4,32 ) m/s2
1,05m
Xm
Vox=4m/s

75. Una pelota de tenis se impulsa con una raqueta de tal modo que su
velocidad inicial es 56i km/h, desde el borde de una cancha que mide
23,77m de largo y desde una altura de 2,5m. Determinar: a) La
distancia a la que rebota la primera vez respecto de la red central cuya
altura de 0,92m. b) La velocidad mínima que se le debe comunicar a la
pelota para que justamente logre pasar la red. c) la velocidad que se le
debe comunicar a la pelota para que caiga justamente al borde
opuesto de la cancha. Sol: a) 11.05m. b) 20,86 m/s2. c) 33,48 m/s2.

76. Se lanza un proyectil desde un punto de coordenadas (4,3) m con una
velocidad de (15i +12j ) m/s. Determinar: a) La aceleración, velocidad y
posición para cualquier tiempo. b) El tiempo de vuelo. c) El alcance
horizontal. d) La altura máxima. e) La velocidad del proyectil en 1 s. f)
La aceleración tangencial y la centrípeta en 1 s. Solución: b)2,68s.
c)44,20m. d)10,35m. e) (15; 2,2 )m/s. f) (-1,4; -0,2 )m/s2; (-1,4; 9,6 )m/s2.
4
3
jtiV )8,912(15 


77. Un bombardero que vuela horizontalmente a 5000 m de altura y con
una rapidez de 450 m/s trata de atacar a un barco que navega a 38 m/s
en la misma dirección y sentido que el avión. Determinar: a) A qué
distancia detrás de la popa del barco debe dejar caer la bomba para
lograr hacer impacto. b) Con qué velocidad hará impacto.
m3,13159

78. Se lanza un balón de tal manera pasa exactamente sobre dos barreras
cada una de 2 m de altura que están separadas 10m. Si el tiempo que
demora el balón en recorrer la distancia entre las barreras es 1s;
determinar:
a)La velocidad inicial con que fue lanzado el balón.
b)La altura máxima.
c)El alcance horizontal.
d) EL tiempo total desde que es lanzado hasta que llega al nivel de
lanzamiento.
Xm
Vx
Vy
V


smjiV /)96,710(

 mh 23,3 mXm 2,16 mt 62,1

79. Se lanza un proyectil balístico intercontinental con un alcance máximo
de 10.000 Km. Hacia una ciudad y es detectado con el radar por
primera vez cuando se encuentra en la mitad de su recorrido.
Determinar: a) Con que velocidad fue disparado. b) De cuánto tiempo
se dispone para dar aviso. c) Que velocidad lleve el proyectil cuando se
lo detecta. d) Con que velocidad pegara en el blanco. e) Cual es su
altura máxima.
10000Km
VoyVox
SenVVoy
CosVVox



º45.
º45.
vuelo
vuelo
tVoy
tVoxx
.10000000
.max


Vx
Vy
V
º45
jiV
jVoyiVoxVa



)
0
2
1
. 2
 gtvtvVoyh

80. Una persona con patines sube por una rampa de 20º, cuando abandona la
rampa, salta hasta una grada situada a 2m de distancia horizontal y 0,5m abajo
del punto donde abandona la rampa; determinar
a) La velocidad mínima con la que debe abandonar la rampa para llegar
justamente a la grada sin problema.
b) La máxima altura que alcanza desde el punto donde abandona la rampa.
c) Si con la misma rapidez calculada en el punto a) abandona una rampa de 15º,
¿Lograra alcanzar la grada sin problema?
2m
nocmbjiVa )....11,0))....45,14()


V
º20
Vx
Vy

82. radrev .2º3601 
VARIABLES ANGULARES SIMBOLO UNIDADES
Posición angular θo rad
Desplazamiento angular Δθ rad
Velocidad angular instantánea ω rad/s
Aceleración angular α rad/s2
t. 
t




or

fr

o
f


83. MOVIMIENTO→CAMBIO DE POSICION
CIRCULAR→DIRECCION VARIABLE
UNIFORME→MODULO CONSTANTE
velocidad angular ω es constante.
La aceleración angular α es nula.
FORMULA
t





 rad
T
2

T
f
1
 T
R
V
.2

Rac .2

R
v
v
v
v
v
v
v
v
ac

85. Una partícula parte de un punto (-3,4) cm, moviéndose en sentido
antihorario sobre una trayectoria circular con centro en el origen, con
una velocidad angular constante de 4 rad/s. a) La posición angular
inicial. b) El desplazamiento angular en 10 s. c) La posición angular
final. d) La posición final.
rad
cmr
cmra
o
o
o
21,2
º180
º.9,126
)º9,126;5(
)4,3()







radssrad
tb
4010./4
.)




radc of 21,42)  
cmjir
cmrd
f
f
)9,4001,1(
)º45,2418;5()





86. Una partícula se mueve por una trayectoria circular de 1,2 m. de radio, gira un ángulo de 225°
cada 15 segundos. Determinar: a) La velocidad angular de la partícula. b) La rapidez de la
partícula. c) El período. d) La frecuencia. e) El módulo de la aceleración centrípeta.
srad
s
rad
t
a
/26,0
15
93,3
)









s
m
V
m
s
rad
V
RVb
31,0
2,126,0
.)


 
sT
s
rad
rad
T
rad
Tc
17,24
26,0
.2
2
)






2
2
2
/08,0
2,1)/26,0(
.)
sma
msrada
Rae
c
c
c



Hzsf
s
f
T
fd
o04,0
17,24
1
1
)
1



st
rad
rad
DATOS
15
93,3
º180
.
º.225





87. Un volante cuyo diámetro es de 0,10 m está girando a 20RPS. Determinar: a) La velocidad
angular b) El período c) La frecuencia d) La rapidez de un punto del borde e) El módulo de la
aceleración centrípeta
srad
v
rad
s
v
a
/66,125
Re1
2
.
Re
20)





sT
s
rad
rad
T
rad
Tb
05,0
40
.2
2
)







Hzsf
s
f
T
fc
o1
20
05,0
1
1
)



 s
m
V
m
s
rad
V
RVd
28,6
05,066,125
.)


 
2
2
2
/52,789
05,0)/66,125(
.)
sma
msrada
Rae
c
c
c


 

88. Un cuerpo parte del punto (-2, 6)m y gira en sentido antihorario a 500 RPM
durante 4 s. Si el centro de la circunferencia está en el origen, determinar: a) La
velocidad angular. b)La posición angular inicial. c) La posición angular final. d)
La posición final. e) Cuántas vueltas da en los 4 s. f) El período. g) La velocidad
en la posición inicial. h) La aceleración centrípeta en la posición inicial.
srad
sv
radv
a
/36,52
60
min1
.
Re1
2
.
min
Re
500)





rad
rad
mr
mrb
o
o
o
89,1
º180
º.43,108
)º43,108;32,6(
)6,2()






radradrad
rads
s
rad
t
c
f
of
of
33,21189,144,209
44,209436,52.
)








mr
rad
rad
RPmrd
f
f
f
)72,4;20,4(
º32,12108
º180
33,211
)º32,12108;32,6()







rev
rad
rev
rade 33,33
2
1
44,209) 


s
rad
Tf 12,0
.2
) 


smjiV
smV
smV
m
s
rad
V
RVg
/)62,10495,313(
)º43,198;/92,330(
/92,330
32,636,52
.)








jia
jisma
uaa
sma
msrada
Rah
c
c
rocc
c
c
c



38,1646055,5544
)95,032,0(/72,17326
)(
/72,17326
32,6)/36,52(
.)
2
2
2
2





 

89. El sol efectúa un movimiento de translación a través de la Vía láctea; el radio de la órbita
es 2,4 x 1020 m y su período de revolución es de 6,3 x 1015 s. Determinar, a) La frecuencia
b) La distancia recorrida en 50 años en Km. c) La velocidad angular d) La rapidez en
Km./h e) El módulo de la aceleración centrípeta.
Hzsf
s
f
T
fa
o116
15
1059,1
103,6
1
1
)





kmd
kmd
Perimetrond
vueltan
s
horadia
horas
año
dias
añosb
10
177
715
1070,37
)104,22(1050,2
1050,2103,61576800000
1576800000
1
3600
.
1
24
.
1
365
.50)








s
rad
s
rad
T
rad
c
16
15
1097,9
103,6
2
2
)










h
km
V
km
hora
s
s
rad
V
RVd
861408
104,2.
1
3600
.1097,9
.)
1716





210
20216
2
/1039,2
104,2)/1097,9(
.)
sma
msrada
Rae
c
c
c




 

90. MOVIMIENTO→CAMBIO DE POSICION
CIRCULAR→DIRECCION VARIABLE
UNIFORMEMENTE VARIADO→MODULO
VARIABLE
v
v
v
v
v
v
v
v
ac
at
aT
to . 
2
.
2
1
tto  
  .2
22
oRaT .Rac .2


91. Una partícula parte del reposo desde el punto A(3cm; NE) en sentido antihorario
con una aceleración tangencial constante de 5cm/s2 y gira un ángulo de (7π/3)
rad en una trayectoria circular. Determinar: a) La aceleración angular. b) La
velocidad angular final. c) El tiempo empleado. d) La posición angular final. e) La
posición final. f) La velocidad final. g) La aceleración total final.
st
tc o
96,2
67,1
95,4
.)

 
2
/67,1
3
5
.)
srad
Raa T




srad
b o
/95,43/767,12
.2)
22




rad
rad
radd
f
of
o
12,8
43
7
33,7
3
7
79,0
º180
º.45)











cmjir
cmr
rad
rade
f
f
f
)89,279,0(
)º24,465;3(
º24,465
.
º180
.12,8)







scmjiV
scmcm
s
rad
V
RVf f
/)91,333,14(
/85,14395,4
.)



 
2
22
22
222
/68,73
51,735
51,73395,4.
)
scma
a
Ra
aaag
c
CT





rad
scma
cmR
cmr
DATOS
T
o
3
7
/5
3
)º45;3(
0
2
0










92. La velocidad angular de una turbina disminuye uniformemente de 800 RPM a
300 RPM en 10s. Si el radio de la curvatura es de 1 cm., determinar: a) La
rapidez inicial. b) La aceleración angular. c) El desplazamiento angular d)
Cuántas vueltas da. e) Qué tiempo será necesario para que la turbina se
detenga
scmV
cmsradV
RVa o
/78,83
1/78,83
.)


 
2
/24,5
10
78,8341,31
)
srad
t
tb
of
of











rad
ttc o
8,575
)10)(24,5(
2
1
)10(78,83
.
2
1
)
2
2






st
t
t
te
of
of
99,15
24,5
78,830
)










vueltas
rad
rev
radd
64,91
2
1
.8,575)






94. 1TALLER
Una partícula se desplaza −𝟑𝟎𝒊 + 𝟒𝟎 𝒋 𝒎, con
velocidad constante, durante 1 minuto.
Determinar:
a)La distancia recorrida en m
b)La velocidad en m/s.
c)La rapidez en m/s.
d)El vector unitario de la velocidad,
e)El vector unitario del desplazamiento.

95. Un cuerpo es lanzado hacia arriba con
una rapidez de 20m/s.
Determinar:
a)En que instante la velocidad será de
6m/s.
b)A que altura se encontrará.
a) 1,43s; 18,58m.
b) 1,59s; 19,89m.
c) 2,05s; 20,01m
d) 2,12s; 21,99m

96. Con que velocidad inicial fue
lanzado un cuerpo que cuando ha
subido 5cm posee una velocidad
de 200cm/s. Qué tiempo ha estado
subiendo.
a) 200
b) 2231,1cm/s; 0,02s