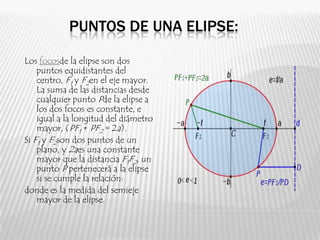
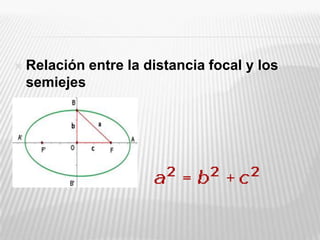
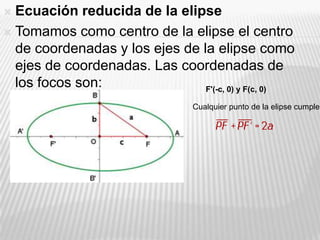
Este documento describe las propiedades geométricas de una elipse. Explica que una elipse es una curva cerrada simétrica definida como el conjunto de puntos cuya suma de distancias a dos focos (puntos fijos) es constante. Detalla los elementos clave de una elipse como sus ejes, vértices, centro y focos; y cómo se puede representar mediante una ecuación. Finalmente, proporciona ejemplos para ilustrar estas propiedades.

1. GEOMETRÍA
ANALÍTICA

2. INTEGRANTES
Joselyne Salcedo García
 Marisol Nuño Arriaga
 Mónica Yarely Torres Urenda
 Fátima Lourdes Bolaños Hernández
 Martha Lizbeth García Rivera

3. QUE ES UN ELIPSE:
 Una elipse es la curva simétrica cerrada que
resulta al cortar la superficie de un cono por un
plano oblicuo al eje de simetría –con ángulo
mayor que el de la generatriz respecto del eje de
revolución.[1] Una elipse que gira alrededor de
su eje menor genera un esferoide achatado,
mientras que una elipse que gira alrededor de su
eje principal genera un esferoide alargado.

4. EJEMPLO:

5. ELEMENTOS DE UNA ELIPSE
La elipse y algunas de sus propiedades
matemáticas.
La elipse es una curva plana y cerrada, simétrica
respecto a dos ejes perpendiculares entre sí:
El semieje mayor (el segmento C-a de la
figura), y
el semieje menor (el segmento C-b de la figura).
Miden la mitad del eje mayor y menor
respectivamente.

6. …
 Focos :
Son los puntos fijos F y F'.
 Eje focal :
Es la recta que pasa por los focos.
Eje secundario :
Es la mediatriz del segmento FF'.

7.  Centro :
Es el punto de intersección de
los ejes.
 Radios vectores :
Son los segmentos que van
desde un punto de la elipse a
los focos:PF y PF'
 Distancia focal :
Es el segmento de longitud
2c, ces el valor de la
semidistancia focal.

8. …
 Vértices :
Son los puntos de
intersección de la elipse
con los ejes: A, A', B y B'.
 Eje mayor :
Es el segmento de longitud
2a, aes el valor del semieje
mayor.
 Eje menor :
Es el segmento de longitud
2b, bes el valor del semieje
menor.

9.  Ejes de simetría :
Son las rectas que
contienen al eje mayor
o al eje menor.
 Centro de simetría:
Coincide con el centro de
la elipse, que es el punto
de intersección de los
ejes de simetría.

10. PUNTOS DE UNA ELIPSE:
Los focosde la elipse son dos
puntos equidistantes del
centro, F1 y F2en el eje mayor.
La suma de las distancias desde
cualquier punto Pde la elipse a
los dos focos es constante, e
igual a la longitud del diámetro
mayor, (PF1 + PF2 = 2a).
Si F1 y F2son dos puntos de un
plano, y 2aes una constante
mayor que la distancia F1F2, un
punto P pertenecerá a la elipse
si se cumple la relación:
donde es la medida del semieje
mayor de la elipse.

11. EJES DE UNA ELIPSE
 El eje mayor 2a, es la mayor distancia entre dos
puntos adversos de la elipse. El resultado
constante de la suma de las distancias de
cualquier punto a los focos equivale al eje
mayor. El eje menor 2b, es la menor distancia
entre dos puntos adversos de la elipse. Los ejes
de la elipse son perpendiculares entre si.

12. CONSTANTE DE LA ELIPSE
 En la figura de la derecha se muestran
los dos radio vectores
correspondientes a cada punto P de
una elipse, los vectores que van de los
focos F1 y F2 a P. Las longitudes de los
segmentos correspondientes a cada
uno son PF1 (color azul) y PF2(color
rojo), y en la animación se ilustra
como varían para diversos puntos P de
la elipse.
 Como establece la definición inicial de
la elipse como lugar geométrico, para
todos los puntos P de la elipse la suma
de las longitudes de sus dos radio
vectores es una cantidad constante
igual a la longitud 2a del eje mayor:
 PF1 + PF2 = 2a En la elipse de la
imagen 2avale 10 y se ilustra, para un
conjunto selecto de puntos, cómo se
cumple la definición.

13. DIRECTRICES DE LA ELIPSE
 La recta dDes una de las 2 directrices de la elipse.
Cada foco F de la elipse está asociado con una recta paralela
al semieje menor llamada directriz (ver ilustración de la
derecha). La distancia de cualquier punto P de la elipse
hasta el foco Fes una fracción constante de la distancia
perpendicular de ese punto Pa la directriz que resulta en
la igualdad:
La relación entre estas dos distancias es la excentricidad de
la elipse. Esta propiedad (que puede ser probada con la
herramienta esferas de Dandelin) puede ser tomada
como otra definición alternativa de la elipse.

14.  Relación entre la distancia focal y los
semiejes


15. 

16.  Ecuación reducida de la elipse
 Tomamos como centro de la elipse el centro
de coordenadas y los ejes de la elipse como
ejes de coordenadas. Las coordenadas de
los focos son: F'(-c, 0) y F(c, 0)
Cualquier punto de la elipse cumple:

17. Esta expresión da lugar a:
Realizando las operaciones
llegamos a:

18. EJEMPLO
 Hallar los elementos característicos y la
ecuación reducida de la elipse de focos: F'(-
3,0) y F(3, 0), y su eje mayor mide 10.

19.  http://www.geoan.com/conicas/ecuacion_elip
se.html
 http://es.wikipedia.org/wiki/Elipse
 http://www.ditutor.com/geometria_analitica/eli
pses.html

20. ECUACION DE LA ELIPSE VIDEO
 http://www.youtube.com/watch?v=KbUv71ehgp
M