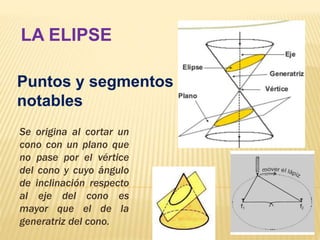
El documento describe las características geométricas de una elipse. Explica que una elipse se origina al cortar un cono con un plano inclinado respecto al eje del cono. Luego enumera los elementos clave de una elipse como los focos, el eje mayor y menor, la excentricidad, y provee las ecuaciones para describir una elipse general y una elipse con ejes paralelos a los ejes de coordenadas.

1. Se origina al cortar un
cono con un plano que
no pase por el vértice
del cono y cuyo ángulo
de inclinación respecto
al eje del cono es
mayor que el de la
generatriz del cono.
Puntos y segmentos
notables
LA ELIPSE

2. En toda elipse se pueden
distinguir los siguientes
elementos:
F y F´: Son los puntos fijos
llamados focos. Son equidistantes
del equidistantes al centro
2c: Se le llama distancia focal y
es la distancia que hay entre los
dos focos.
P: Cualquier punto de la elipse.
PF y PF´: Son los radio vectores
de la elipse.
2a: Es la suma de los radio
vectores.

3. Eje focal: Es la recta que
pasa por los focos.
Eje secundario: Es la
mediatriz del segmento
C: Es el centro de la Elipse.
B y B’ A y A’ : Son los vértices
de la elipse.
AA’: Es el eje mayor de la
elipse y su longitud es 2a
BB’: Es el eje menor de la
elipse y su longitud es 2b.

4. LA EXENTRICIDAD
a
Es la razón entre su semidistancia
focal (centro de la elipse a uno de
sus focos) c y su semieje mayor
a. Su valor se encuentra entre
cero y uno

5. LADO RECTO
LR = 2b² .
a
Es la cuerda perpendicular al eje
mayor y que pasa por el foco.

6. ANÁLISIS DE LA ECUACIÓN
Ecuación de la
Elipse con centro
en el origen y ejes
de coordenadas los
ejes de la elipse.

7. TEOREMA 1.
• La ecuación de una elipse de
centro en el origen, eje focal el
eje X, distancia focal igual a 2c
y cantidad constante igual a 2a
es:
• Si el eje focal de la
elipse coincide con el
eje Y, de manera que las
coordenadas de los
focos sean (0,c) y (0, -c),
la ecuación de la elipse
es:

8. • PARA CADA ELIPSE , LA LONGITUD DE CADA LADO
RECTO ES:
• La excentricidad e está dada por la fórmula:

9. Ecuación de la
Elipse de centro
(h,k) y ejes
paralelos a los
coordenados.

10. TEOREMA 2.
• La ecuación de la elipse de
centro (h,k) y eje focal paralelo
al eje X , está dada por la
segunda forma ordinaria.
• Si el eje focal es
paralelo al eje Y, su
ecuación está dada por
la segunda forma
ordinaria:

11. TEOREMA 3.
• Si los coeficientes A y C son del mismo signo, la ecuación
Representa una elipse de ejes paralelos a los coordenados, o
bien un punto, o no representa ningún lugar geométrico real.
PROPIEDADES DE LA ELIPSE
TEOREMA 4.
• La tangente a la elipse en
cualquier punto de la curva, tiene por
ecuación:

12. TEOREMA 5.
• Las ecuaciones de las tangentes de pendiente m a la
elipse
son:
TEOREMA 6.
• La normal a una elipse en un punto
cualquiera de sus puntos es
bisectriz del ángulo formado por los
radios vectores de ese punto.

13. EJERCICIOS DE
APLICACION

14. 1. Halle la ecuación de la elipse que tiene su centro en (0, 0) y cuyos
focos son los puntos F(, 0) y F’(-3, 0), además el intercepto de la
gráfica con el eje x es el punto (5, 0).
Solución:
Como la elipse corta al eje x en el punto (5, 0) se sigue que a = 5 y
como c = 3 (fig. 6.5.8) se tiene que,
y por tanto
De esta forma, los vértices de la elipse son los puntos V1(5, 0), V2(-
5, 0), V3(0, 4) y
V4(0, -4). Además, su ecuación viene dada por :

15. 2.Trazar la elipse cuya ecuación viene dada por:
25x2 + 4y2 = 100
Solución:
La ecuación: 25x2 + 4y2 = 100, puede escribirse en las formas
equivalentes:
x 2 + y 2= 1
4 25
La última ecuación corresponde a una elipse centrada en el
origen cuyo eje mayor es b = 5 y eje menor es a = 2. Además, los
focos de la elipse están localizados sobre el eje y.
De otro lado, , de donde y en consecuencia,
los focos se encuentran localizados en los puntos y
Además, los vértices de la elipse son los puntos: V1(2, 0), V2(5,
0), V3(-2, 0) y V4(-5, 0).

16. 3. Determine el centro, los vértices, los focos y dibujar la elipse que tiene por
ecuación:
4x2 + y2 –16x + 2y + 13 = 0
Solución:
La ecuación dada se puede escribir en las formas equivalentes:
(completación de cuadrado)
(factorización y simplificación)
(dividiendo por 4)
Esta última ecuación corresponde a la elipse cuyo centro es el punto C(2, -1),
semiejes;
a = 1 y b = 2. Como a < b, el eje focal es paralelo al eje y y tiene por
ecuación x = 2
Los vértices son los puntos V1(2, 1), V2(2, -3), V3(3, -1) y V4(1, -1).
Como , se tiene que los focos están localizados en los
putos y

18. ANFITEATRO ROMANO DE POMPEYA
 Es el más antiguo
anfiteatro romano que
sobrevive.
 Se encuentra ubicado
en la antigua ciudad
romana de Pompeya,
y fue enterrado por la
erupción del Vesubio
en el año 79.
 Construido alrededor
del 70 AC, el anfiteatro
actual fue el primer
anfiteatro romano que
se construyó en piedra

19. LA SALA CAPITULAR DE LA CATEDRAL DE
SEVILLA
 La Catedral de Santa María
de la Sede de Sevilla es
la catedral gótica cristiana
con mayor superficie del
mundo.
 La Unesco la declaró
en1987, junto al Real
Alcázar y el Archivo de
Indias, Patrimonio de la
Humanidad y, el 25 de julio
de 2010, Bien de Valor
Universal Excepcional.
 La construcción se inició en
1401, aunque no existe
constancia documental del
comienzo de los trabajos
hasta 1433.

20. ANFITEATRO ROMANO DE LEÓN
 El anfiteatro romano
de León era más
grande que la Plaza
Mayor.
 La investigación
desvela que el circo
habría tenido
capacidad para
cinco mil
espectadores.
 Su superficie
alcanzaba los tres
mil metros
cuadrados y tenía
quince niveles de
graderío.

21. CÓNICAS EN EL PALATINO DE ROMA
 La visión es un
cono con vértice
en nuestro ojo,
la perspectiva
va a cambiar la
forma de los
objetos: en
nuestro caso
invierte los ejes
de la elipse

22. CORRAL DE COMEDIAS
 La Abadía extiende su actividad a
un edificio emblemático,.
 En Madrid, desde 2005 la
Fundación Teatro de La Abadía
se ocupa de la gestión y
programación del Corral de
Comedias de Alcalá.
 Construido en 1601, a la manera
de los desaparecidos teatros
madrileños del Príncipe y la Cruz
-a cielo descubierto, con
empedrado, pozo y desván de
tramoyas-, más tarde este corral.
 Fue techado mediante un
entramado de vigas que mejoró
su acústica, sobre todo para
espectáculos musicales.

23. ANFITEATRO DE POMPEYA
 El Anfiteatro romano de
Pompeya es el más
antiguo anfiteatro romano que
sobrevive.
 Se encuentra ubicado en la
antigua ciudad romana
de Pompeya, y fue enterrado por
la erupción del Vesubio en el
año 79, que también enterró
Pompeya y la vecina Herculano.
 Construido alrededor del 70 AC,
el anfiteatro actual fue el primer
anfiteatro romano que se
construyó en piedra.
 Con anterioridad, habían sido
construidos en madera.
 El siguiente anfiteatro romano
que se construyó en piedra sería
el Coliseo de Roma, que es
posterior a este por más de un
siglo.

24. PLAZA DE SAN PETERSBURGO
 Fue fundada por el zar Pedro el Grande el 16
de mayo de 1703 con el propósito de
deslocalizar la capital ubicada en Moscú, y de
hecho fue capital de Rusia de 1712 a 1918. Por
ello y por su ubicación geográfica le dio el
sobrenombre de "La ventana a Europa".

26. TEMPLO DEL AGUA
TADAO
ANDO
COMPLEJO ELIPSE

28. TORRE ELIPSE

29. PAELLA AND CHIPS