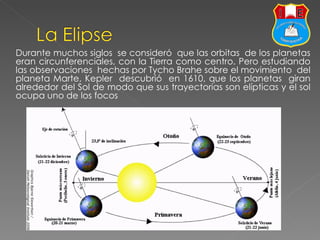
El documento describe los elementos básicos de una elipse, incluyendo sus focos, ejes mayor y menor, excentricidad y ecuación canónica. Explica que las órbitas planetarias descubiertas por Kepler son elípticas, no circulares, y que el Sol se ubica en uno de los focos de cada elipse planetaria.

1. Durante muchos siglos se consideró que las orbitas de los planetas eran circunferenciales, con la Tierra como centro. Pero estudiando las observaciones hechas por Tycho Brahe sobre el movimiento del planeta Marte, Kepler descubrió en 1610, que los planetas giran alrededor del Sol de modo que sus trayectorias son elípticas y el sol ocupa uno de los focos

2. P(x,y) X Y O

3. Los elementos más importantes de la elipse son: FOCOS : Los puntos fijos RECTA FOCAL : La recta a la que pertenecen los focos RECTA SECUNDARIA : La simetral del segmento CENTRO : Punto de intersección de las rectas focal y secundaria y que equidista de los focos . VÉRTICES : Puntos de intersección de la elipse con la recta focal. Se designan:

4. EJE MAYOR : Segmento que se considera de longitud 2 a : a es el valor del semieje mayor . EJE MENOR : Segmento de la recta secundaria interceptada por la elipse . Se considera de longitud 2b : b es el valor del semieje menor. DISTANCIA FOCAL : Medida del segmento Se considera de longitud 2c. LADO RECTO : Cuerda focal perpendicular a la recta focal o eje de simetría . Su medida, como veremos más adelante, es

5. a a c c b a a

6. A toda elipse se le asocia un número real que llamamos EXCENTRICIDAD DE LA ELIPSE, designado por la letra e, y cuyo valor es : Dado que la excentricidad depende de las medidas de c y a , su valor está asociado con la forma de la respectiva elipse , es así que tenemos elipses más o menos achatadas. La excentricidad de la elipse es un número menor que 1. Si c tiende a cero, entonces e también tiende a cero, por lo tanto se forma una circunferencia

7. 4 -4 -3 3 o 5 -4 4 5 Elipse de excentricidad e = Elipse de excentricidad e= o Ejemplo:

8. La ecuación canónica de la elipse es : Centro: C(0;0) 2a cantidad constante Eje focal : Eje “x” Focos: F 1 (-c;0) y F 2 (c;0) , 0 < c < a y X V 2 (a,0) V 1 (-a,0) B 1 (0,b) B 2 (0,-b) P(x,y) (eje focal en el eje X) F 2 (c;0) F 1 (-c;0) C(0;0)

9. La ecuación canónica de la elipse es : Centro: C(0;0) 2a cantidad constante Eje focal : Eje “Y” Focos: F 1 (0;-c) y F 2 (0;c) , 0 < c < a Y X ( Eje focal en el eje Y ) V 1 (0;a) B1(-b;0) P(x,y) F 1 (0;-c) F 2 (0; c) C(0;0) V 2 (0;-a) B 2 ( b;0)

10. Determinar la ecuación de la elipse con focos (0,6) y (0,-6) y semieje menor 8 Solución: eje focal coincide con el eje Y Luego c =6 ; b = 8 y a = 10 La ecuación pedida es :

11. Encontremos los elementos de elipse de ecuación Tenemos a = 5 y b = 3, además C = 4, los elementos de la elipse son : FOCOS: EJE MAYOR : 2 a = 2·5 = 10 EJE MENOR : 2b = 2·3 = 6 LADO RECTO :

12. EXCENTRICIDAD: VERTICES: (5,0) y ( -5,0) y X 3 -3 5 -5 4 -4

13. Sea el centro de la elipse el punto C(h,k) y el eje focal paralelo al eje X h k O Y X La ecuación principal de la elipse con centro en C(h,k ) es:

14. Al desarrollar los cuadrados de binomio, ordenando la ecuación principal de la elipse e igualando a cero, encontramos la ecuación equivalente , llamada ECUACIÓN GENERAL DE LA ELIPSE A<B

15. Dada la ecuación principal de la elipse Determine la ecuación general de la elipse Solución :

16. Determinemos los elementos de la elipse de ecuación: Ordenamos la ecuación para completar los cuadrados de binomio

17. Luego: h=8 y k =-3, (8,-3) además Como esta elipse ha sido trasladada con respecto a su posición canónica, su eje focal también se ha trasladado en h=8 unidades. Por lo tanto, las coordenadas de los focos son:

18. 8 -3 4 12 C(8,-3) X Y