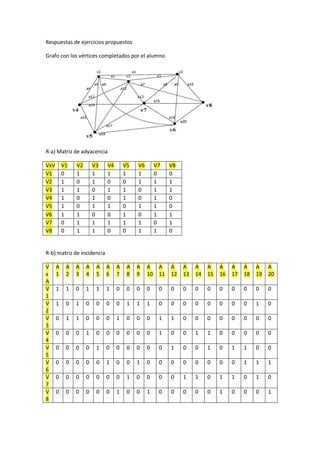
Este documento contiene las respuestas a ejercicios propuestos sobre grafos. Se presentan las matrices de adyacencia y incidencia de un grafo no dirigido, y se demuestra que el grafo es conexo, simple, pero no regular ni completo. También se muestran una cadena y un ciclo del grafo, así como un árbol generador y un subgrafo parcial. Finalmente, se analiza un grafo dirigido y se encuentran su matriz de conexión, una cadena no simple, y un ciclo simple.

1. Universidad Fermín Toro
Extensión Cabudare 2013
Enrique José Rodríguez Quintero
20.927.971

2. Respuestas de ejercicios propuestos
Grafo con los vértices completados por el alumno
R-a) Matriz de adyacencia
VxV
V1
V2
V3
V4
V5
V6
V7
V8
V1
0
1
1
1
1
1
0
0
V2
1
0
1
0
0
1
1
1
V3
1
1
0
1
1
0
1
1
V4
1
0
1
0
1
0
1
0
V5
1
0
1
1
0
1
1
0
V6
1
1
0
0
1
0
1
1
V7
0
1
1
1
1
1
0
1
V8
0
1
1
0
0
1
1
0
R-b) matriz de incidencia
V
x
A
V
1
V
2
V
3
V
4
V
5
V
6
V
7
V
8
A
1
A
2
A
3
A
4
A
5
A
6
A
7
A
8
A
9
A
10
A
11
A
12
A
13
A
14
A
15
A
16
A
17
A
18
A
19
A
20
1
1
0
1
1
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
1
0
0
0
0
1
1
1
0
0
0
0
0
0
0
0
1
0
0
1
1
0
0
0
1
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
1
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
1
0
1
1
0
0
0
0
0
0
0
1
0
0
1
0
0
0
0
0
0
0
0
1
1
1
0
0
0
0
0
0
0
1
0
0
0
0
1
1
0
1
1
0
1
0
0
0
0
0
0
0
1
0
0
1
0
0
0
0
0
1
0
0
0
1

3. R-c) Es conexo? Justifique su respuesta
Si es conexo,
El grafo es conexo ya que todos sus vértices están conectados entre sí, es decir, existe una
cadena ∀ para cada par de vértices.
R-d) Es simple? Justifique su respuesta
Si es simple
Es simple debido a que el mismo no tiene lasos.
R-e) Es regular? Justifique su respuesta
No es regular
El grafo no es regular debido a que todos los vértices no tienen el mismo grado.
R-f) Es completo? Justifique su respuesta
Si es completo
Es completo ya que existen aristas uniendo todos los pares posibles de vértices.
R-g) Una cadena simple no elemental de grado 6
Cadena simple no elemental de grado 6:
C1 = [V1,a4,V4,a15,V5,a12,V3,a13,V7,a8,V2,a1,V1]
O (C1) = 6
R-h) Un ciclo no simple de grado 5
C1 = [V6,a9,V2,a8,V7,a13,V3,a2,V1,a6,V6]
O (C1) = 5

4. R-j) Árbol generador aplicando el algoritmo constructor
V5, H1 = [V5]
ARISTA 17 Y H2= [V5, V7]
ARISTA 14
H3= [V5, V7, V4]
ARISTA 11
H4= [V5, V7, V4, V3]
ARISTA 16
H5= [V5, V7, V4, V3, V8]
ARISTA 20
v6
H6= [V5, V7, V4, V3, V8, V6]
ARISTA 2
H7= [V5, V7, V4, V3, V8, V6, V1]
ARISTA 8
H8= [V5, V7, V4, V3, V8, V6, V1, V2]
R-j) Subgrafo parcial
G= [V4, A4, g4]
V4Cv
A4CA
Subgrafo parcial
R-k) Demostrar si es euleriano aplicando el algoritmo de Fleury
Intentando en reiteradas ocasiones aplicar el algoritmo de fleury, siempre quedaba una arista afuera del
algoritmo, por lo que el grafo no es eureliano.

5. Dado el siguiente dígrafo
R-a) Encontrar matriz de conexión
MC=
0
0
0
1
0
0
1
0
0
0
1
0
1
1
0
0
0
0
0
1
1
0
1
0
1
1
1
0
0
1
0
0
0
1
1
0
R-b) Es simple? Justifique su respuesta
Si es simple
Es simple debido a que no existen lazos en ninguno de los vértices así como tampoco arcos paralelos.
R-c) Encontrar una cadena no simple no elemental de grado 5
T= [V1, a6, V5, a11, V4, a9, V1, a5, V3, a7, V5]
R-d) Encontrar un ciclo simple
C= [V2, a4, V6, a14, V5, a11, V2]