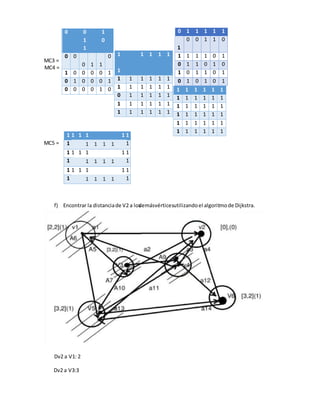
Este documento presenta un ejercicio sobre grafos que incluye varias preguntas: a) encontrar las matrices de adyacencia y de incidencia de un grafo dado, b) determinar si el grafo es conexo, simple, regular o completo, c) encontrar una cadena y un ciclo no simples, d) construir un árbol generador, e) encontrar un subgrafo parcial, f) demostrar si el grafo es euleriano o hamiltoniano. El estudiante procede a responder cada una de las preguntas detallando los cálculos y justificando sus resp

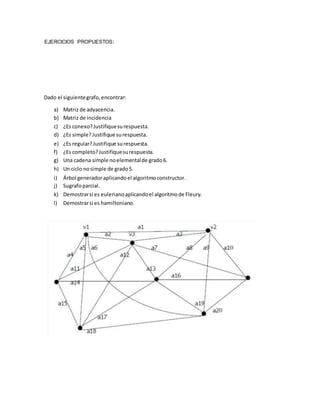

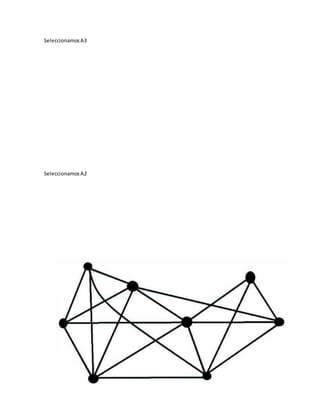
![c) ¿Es conexo?
Si es conexoyaque, segúnladefinición,nosdice
que para cualquier par de vértices(ay b) en(G)
existe al menosuna de las trayectoriasde (a)
(b) donde tienenun caminoque losconecta.
d) ¿Es simple?
Si es simple yaque no posee lazosenningunode
losvértices.
e) ¿Es regular?
Para que sea regularla figuradebe poseer
losmismosgradosy eneste caso, Noesregular,ya
que no todoslosvérticestienenlosmismosgrados.
V1 = 5, V2 = 5, V3 = 6, V4=4, V5 = 6, V6 = 4, V7 = 5, V8 = 5 f)
¿Es completo?
No escompleto,yaque nocumple con ladefiniciónde unaarista,noexistenvértices,ejemplo(V1
y V6) no poseenningunaaristaque losconecten-
g) Una cadena simple noelementalgrado6
C= [V1 a1 V2 a10 V6 a16 V5 a14 V4 a11 V3 A3 V2] indicaque noes elemental,yase repite enel
vértice [v2]
h) Un ciclo de grado 5
C= [v5 a19 v8 a18 v7 a17 c5 a19 v7 a9 v2] Indicaque no essimple porque se repitalaarista[a19].
i) Árbol generadoraplicandoel algoritmoconstructor
• Se elige S1= V1 HaciendoH1=[V1]
V1 V2 V3 V4 V5 V6 V7 V8
A1 1 1 0 0 0 0 0 0
A2 1 0 1 0 0 0 0 0
A3 0 1 1 0 0 0 0 0
A4 1 0 0 1 0 0 0 0
A5 1 0 0 0 1 0 0 0
A6 1 0 0 0 0 0 1 0
A7 0 0 1 0 0 0 0 1
A8 0 1 0 0 0 1 0 0
A9 0 1 0 0 0 0 1 0
A10 0 1 0 0 0 0 0 1
A11 0 0 1 1 0 0 0 0
A12 0 0 1 0 1 0 0 0
A13 0 0 1 0 0 1 0 0
A14 0 0 0 1 0 1 0 0
A15 0 0 0 1 1 0 0 0
A16 0 0 0 0 0 1 0 1
A17 0 0 0 0 1 0 1 0
A18 0 0 0 0 1 0 1 0
A19 0 0 0 0 0 1 1 0
A20 0 0 0 0 0 0 1 1](https://image.slidesharecdn.com/danielarreglado-200116015900/85/Daniel-arreglado-4-320.jpg)
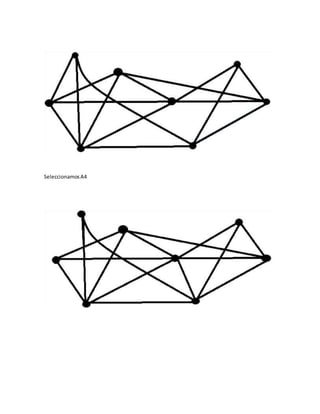
![• Se elige laaristaA4 que se conectaa V1 con V4 haciendoH2= [V1,V4]
V1
A4
V4](https://image.slidesharecdn.com/danielarreglado-200116015900/85/Daniel-arreglado-5-320.jpg)
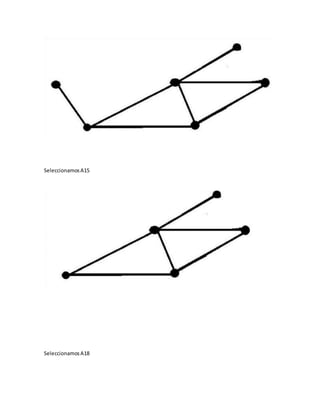
![ElegimoslaaristaA15 que se conectacon V4 con V7 haciendoH3 = [V1,V4, V7].
• Elegimoslaaristaa17 que se conecta con V7 y con V5 haciendoH4 = [V1,V4, V5].
V1
A4
V4
A15
V7
V1
A4
V4 V5
A15 A17
V7](https://image.slidesharecdn.com/danielarreglado-200116015900/85/Daniel-arreglado-6-320.jpg)
![ElegimoslaaristaA19 que se conectaa V5 con V8 haciendoH=5[V1,V4, V8].
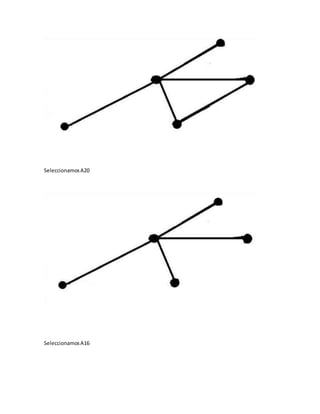
• ElegimoslaaristaA20 que se conectacon V8 con V6 HaciendoH6 = [V1, V4,V7, V5, V8,
V6].
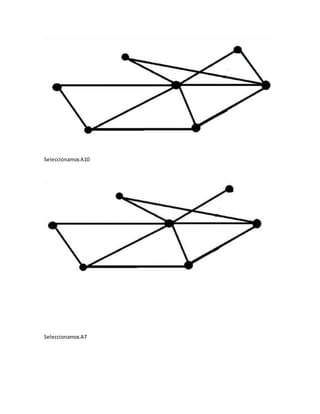
• ElegiremoslaaristaA10 que se conecte con V6 y con V2 HaciendoH7= [V1,V4, V7, V5,V8,
V1
A4
V4 V5
A17 A19
A15 V7 V8
V1
A4
V4 V5 V6
A15 A17 A20
V7 V8](https://image.slidesharecdn.com/danielarreglado-200116015900/85/Daniel-arreglado-7-320.jpg)
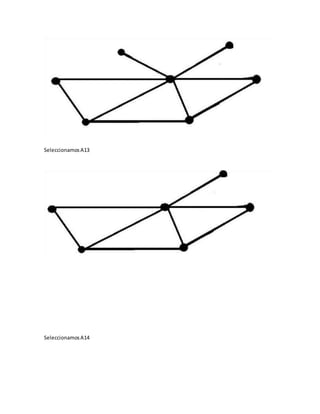
![ElegiremoslaaristaA3 que conectaa V2 con V3 haciendoH8= [V1,V4, V7,V5, V6, V2, V3].
V6, V2].
V1 V2
A4 A10
V4 V5 V6
A15 A17 A20
V7 V8
V3
A3
V1 V2
A4 A10
V4 V5 V6
A19
A15 A17 A20
V7 V8](https://image.slidesharecdn.com/danielarreglado-200116015900/85/Daniel-arreglado-8-320.jpg)
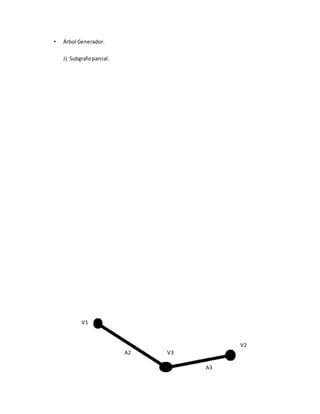
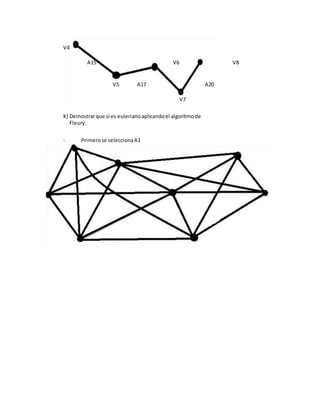
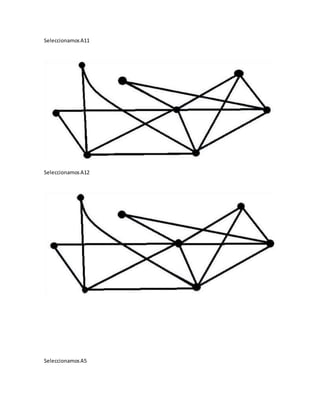
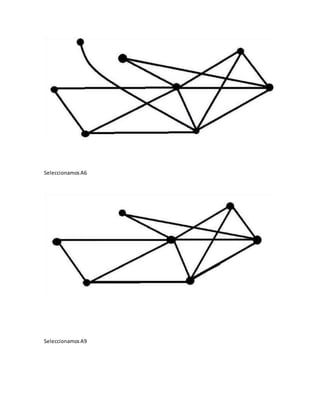

![c) Encontrar una cadenano simple noelementalde grado5.
C= [V1 A6 V5 A11 V4 A12 V6 A14 V5 A13 V6]
d) Encontrar un ciclosimple.
C=[V5 A11 V4 A12 V6 A14 V5]
e) Demostrarsi es fuertemente conexoutilizandolamatrizde accesibilidad.
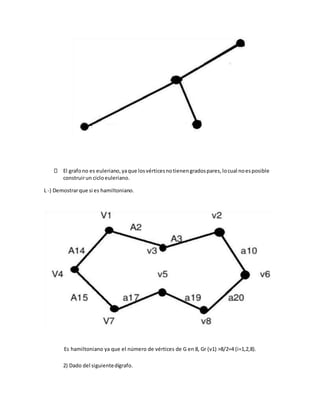
MC = MC2=](https://image.slidesharecdn.com/danielarreglado-200116015900/85/Daniel-arreglado-21-320.jpg)