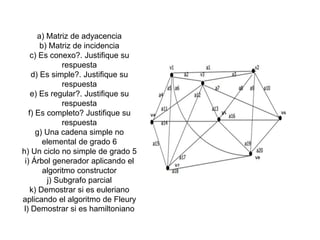
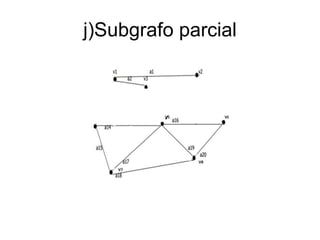
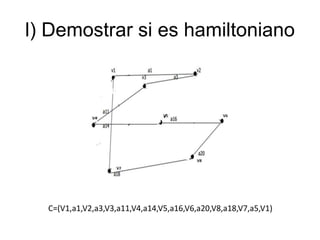
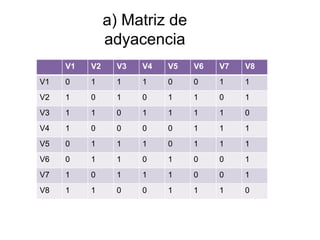
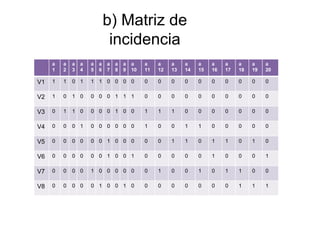
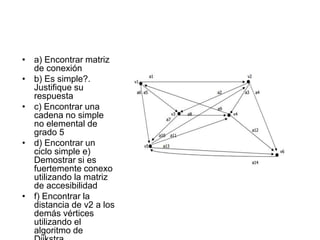
El documento contiene varias preguntas y tareas relacionadas con grafos: a) Encontrar la matriz de conexión y adyacencia del grafo. b) Determinar si el grafo es simple o no, justificando la respuesta. c) Encontrar una cadena no simple no elemental de grado 5 en el grafo.

1. a) Matriz de adyacencia
b) Matriz de incidencia
c) Es conexo?. Justifique su
respuesta
d) Es simple?. Justifique su
respuesta
e) Es regular?. Justifique su
respuesta
f) Es completo? Justifique su
respuesta
g) Una cadena simple no
elemental de grado 6
h) Un ciclo no simple de grado 5
i) Árbol generador aplicando el
algoritmo constructor
j) Subgrafo parcial
k) Demostrar si es euleriano
aplicando el algoritmo de Fleury
l) Demostrar si es hamiltoniano

2. V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 0 0 1 1
V2 1 0 1 0 1 1 0 1
V3 1 1 0 1 1 1 1 0
V4 1 0 0 0 0 1 1 1
V5 0 1 1 1 0 1 1 1
V6 0 1 1 0 1 0 0 1
V7 1 0 1 1 1 0 0 1
V8 1 1 0 0 1 1 1 0
a) Matriz de
adyacencia

3. a
1
a
2
a
3
a
4
a
5
a
6
a
7
a
8
a
9
a
10
a
11
a
12
a
13
a
14
a
15
a
16
a
17
a
18
a
19
a
20
V1 1 1 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
V2 1 0 1 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0
V3 0 1 1 0 0 0 0 1 0 0 1 1 1 0 0 0 0 0 0 0
V4 0 0 0 1 0 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0
V5 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 1 1 0 1 0
V6 0 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 0 0 0 1
V7 0 0 0 0 1 0 0 0 0 0 0 1 0 0 1 0 1 1 0 0
V8 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 1 1 1
b) Matriz de
incidencia

4. c) Es conexo?. Justifique su respuesta
Si es conexo, por que según la teoría tenemos que un grafo es conexo
si cada par de sus vértices están conectados y en el grafo claramente
se puede ver que todos están conectados.
d) Es simple?. Justifique su respuesta
No, en la teoría tenemos que un grafo es simple si solo una arista esta
uniendo a 2 vértices cualesquiera, pero en el grafo dado tenemos que
hasta 4 aristas unen a un vértice.
e) Es regular?. Justifique su respuesta
No, en la teoría tenemos que un grafo es regular cuando cada vértice
tiene el mismo grado o valencia, en el grafo estudiado podemos notar
que los vértices no comparten esta similitud.
f) Es completo? Justifique su respuesta
No, se tiene que un grafo completo es aquel que tiene una arista
conectada a cada vértice
g)Una cadena simple no elemental de grado 6
C=(V1,a4,V4,a11,V3,A3,V2,a8,V5,a13,V3,a18).
h) Un ciclo no simple de grado 5
C=(V1,a1,V2,a10,V6,a7,V3,a3,V2,a1,V1)

5. i) Árbol generador constructor

6. j)Subgrafo parcial

7. l) Demostrar si es hamiltoniano
C=(V1,a1,V2,a3,V3,a11,V4,a14,V5,a16,V6,a20,V8,a18,V7,a5,V1)

8. • a) Encontrar matriz
de conexión
• b) Es simple?.
Justifique su
respuesta
• c) Encontrar una
cadena no simple
no elemental de
grado 5
• d) Encontrar un
ciclo simple e)
Demostrar si es
fuertemente conexo
utilizando la matriz
de accesibilidad
• f) Encontrar la
distancia de v2 a los
demás vértices
utilizando el
algoritmo de

9. a) Encontrar matriz de conexión
b) Es simple?. Justifique su respuesta
c) Encontrar una cadena no simple no
elemental de grado 5
C=(V5,a11,V4,a9,V1,a6,V5,a13,V6,a14,V5
)
d) Encontrar un ciclo simple
C=(V1,a6,V5,a11,V4,a9,V1)
e) Demostrar si es fuertemente conexo
utilizando la matriz de accesibilidad
f) Encontrar la distancia de v2 a los demás
vértices utilizando el algoritmo de Dijkstra