El documento presenta una serie de ejercicios sobre grafos, incluyendo calcular la matriz de adyacencia y incidencia de un grafo dado, determinar si es conexo, simple, regular, completo, encontrar una cadena y ciclo en el grafo, construir un árbol generador, encontrar un subgrafo parcial, y demostrar si es euleriano o hamiltoniano aplicando diferentes algoritmos. Se provee la solución detallada a cada uno de los ejercicios planteados sobre el grafo dado.

1. REPUBLICA BOLIVARIANA DE VENEZUELA
UNIVERSIDAD FERMIN TORO
VICERECTORADO ACADEMICO FACULTAD DE INGENIERIA
ESCUELA DE COMPUTACION
EJERCICIOS PROPUESTOS
ALUMNA:
Fabiola Rodríguez Reyes
C.I: V-24.397.774
Estructuras Discretas II
Prof: Edecio Freitez
Barquisimeto junio de 2016

2. EJERCICIOS PROPUESTOS
Dado el siguiente grafo, encontrar:
a) Matriz de adyacencia
b) Matriz de incidencia
c) ¿Es conexo? Justifique su respuesta
d) ¿Es simple? Justifique su respuesta
e) ¿Es regular? Justifique su respuesta
f) ¿Es completo? Justifique su respuesta
g) Una cadena simple no elemental de grado 6
h) Un ciclo no simple de grado 5
i) Árbol generador aplicando el algoritmo constructor
j) Subgrafo parcial
k) Demostrar si es euleriano aplicando el algoritmo de Fleury
l) Demostrar si es hamiltoniano
Matriz de adyacencia
V1 V2 V3 V4 V5 V6 V7 V8
V1 0 1 1 1 0 0 1 1
V2 1 0 1 0 1 1 0 1
V3 1 1 0 1 1 1 1 0
V4 1 0 1 0 1 0 1 0
V5 0 1 1 1 0 1 1 1
V6 0 1 1 0 1 0 0 1
V7 1 0 1 1 1 0 0 1
V8 0 1 0 0 1 1 1 0

3. b) Matriz de Incidencia
V-A V1 V2 V3 V4 V5 V6 V7 V8
A1 1 1 0 0 0 0 0 0
A2 1 0 1 0 0 0 0 0
A3 0 1 1 0 0 0 0 0
A4 1 0 0 1 0 0 0 0
A5 1 0 0 0 0 0 1 0
A6 1 0 0 0 0 0 0 1
A7 0 0 1 0 0 1 0 0
A8 0 1 0 0 1 0 0 0
A9 0 1 0 0 0 0 0 1
A10 0 1 0 0 0 1 0 0
A11 0 0 1 1 0 0 0 0
A12 0 0 1 0 0 0 1 0
A13 0 0 1 0 1 0 0 0
A14 0 0 0 1 1 0 0 0
A15 0 0 0 1 0 0 1 0
A16 0 0 0 0 1 1 0 0
A17 0 0 0 0 1 0 1 0
A18 0 0 0 0 0 0 1 1
A19 0 0 0 0 1 0 0 1
A20 0 0 0 0 0 1 0 1
c) El grafo es conexo debido a que sus vértices se pueden conectar entre sí.
d) Se puede decir que es simple ya que el grafo como se ve no presenta vértices y no hay
más aristas entre un par de vértices. Están unidos solo por una arista.
e) El grado del grafo que hemos estudiado no es regular por el grado de incidencia, por lo
tanto se puede decir que para que un grafo sea regular todos sus vértices deben tener el
mismo grado de incidencia.
f) Es completo ya que se tiene una arista entre cada par de vértices, como es el caso del
vértice V1 que no está conectado al vértice V5, cada vértice debe estar conectado a
cualquier otro vértice distinto.
g) C1= {v1, a5, v7, a17, v5, a19, v8, a9, v2, a8, v5, a13,v3} Gr(C1)=6
h) {v1, a4, v4, a15, v7, a17, v5, a14, v4, a4, v1}
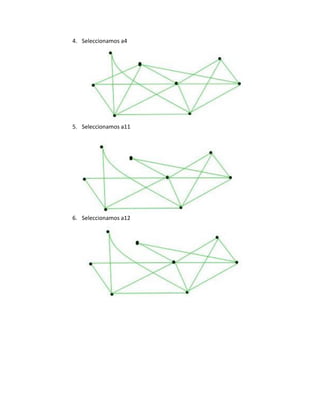
i) Paso 1: Seleccionar v4, H1=[V4]
Paso 2: Seleccionar arista 11, H2=[V4,V3]

4. V3
a11
V4
Paso 3: seleccionar v1, H3=[V4,V3,V1] y arista 2
V1 a1
V3
a11
V4
Paso 4: Seleccionar V2, arista 1 H4=[V4,V3,V1,V2]
v2
V1 a1
A2
v3
a11
v4
Paso 5: seleccionar arista 7, v6 H=[V4,V3,V1,V5,V6]
v2
a1
v1
a2 a7
v3 v6
a11
v4
Paso 6: seleccionar arista 20 y v8 H=[V4,V3,V1,V5,V6,V8]
v2
a1
v1
a2 a7 v6
v3
a11 a2
v4
v8
Paso 7: seleccionar arista 12 y v7 H=[V4,V3,V1,V5,V6,V8,V2]

5. v2
a1
v1 a2 a7 v6
v3
a11 a12 v5 a20
v4 a14
v7 v8
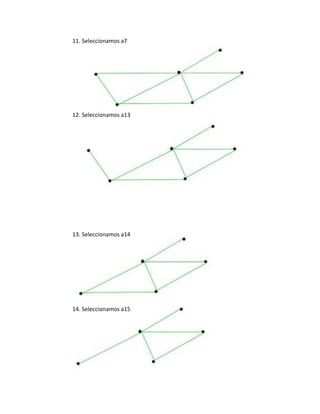
j) v1 a1 v2
a4 a10
v6
v4 v3
a13
a15
v5 a19 v8
v7
l) c=[V1,a1,v2,a10,v6,a20,v8,a18,v7,a15,v4,a14,v5,a13,v8,a2,v1]
v1 a1 v2
a10
v6
a2
v8 a13 a20
v5
a14
v4
a15
v7 a18 v8
k) Demostrar si es Euleriano

6. 1. Seleccionamos a1
2. Seleccionamos a3
3. Seleccionamos a2

7. 4. Seleccionamos a4
5. Seleccionamos a11
6. Seleccionamos a12

8. 7. Seleccionamos a5
8. Seleccionamos a6
9. Seleccionamos a9
10. Seleccionamos a10

9. 11. Seleccionamos a7
12. Seleccionamos a13
13. Seleccionamos a14
14. Seleccionamos a15

10. 15. Seleccionamos a18
16. Seleccionamos a20
ACTIVIDAD 2
a) Matriz de conexión
V1 V2 V3 V4 V5 V6
V1 0 1 1 0 1 0
V2 0 0 1 1 0 1
V3 0 0 0 1 1 0
V4 1 0 0 0 0 1
V5 0 1 0 0 0 1
V6 0 0 0 0 1 0
b) Se puede decir que es simple porque en el dígrafo no existen lazos ni arcos
paralelos
c) Encontrar una cadena no simple no elemental de grado 5:
C={v2,a4,v6,a14,v5,a13,v6,a14,v5,a11,v4,a5,v1}
d) Encontrar un ciclo simple C={v1,a1,v2,a3,v4,a9,v1}

11. e) Demostrar si es fuertemente conexo utilizando la matriz de accesibilidad
M=
0 1 1 0 1 0
0 0 1 1 0 1
0 0 0 1 1 0
1 0 0 0 0 1
0 1 0 1 0 1
0 0 0 0 1 0
M2=
0 1 1 1 1 1
1 0 0 1 1 1
1 1 0 1 0 1
0 1 1 0 1 0
0 1 0 1 0 1
M3=
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
0 1 1 1 1 1
1 1 1 1 1 1
1 0 1 1 1 1
M4=
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
f) Encontrar la distancia de v2 a los demás vértices utilizando el algoritmo de Dijkstra
Pasos Vértices Datos a
Desarrollar
Calculo de di+l Selección v*l+l
Vo=[v2] Vo*=v2
Do[vo*]=0

12. 0
Do[V1]=
infinito
Do[V2]=
infinito
Do[V3]=
infinito
Do[V4]=
infinito
Do[V5]=
infinito
D1[V1]=
infinito
D1[V3]= 3
D1[V4]= 4
D1[V5]=
infinito
D1[V6]= 3
V1*=V3
1
V1=[v2,v1] Vl*= V3
D1[vl*]= 3
D1[v4]= 4
D1[v5]=
infinito
D1[v6]= 3
D2[V1]=
infinito
D2[V4]= 4
D2[V5]= 7
D2[V6]=
infinito
V2*= V4
2 V4=[v2,v3,v2*]
V2*= V4
D2[v1]=
infinito
D2[v4]=
infinito
D2[v6]=
infinito
D2[V2*]= 4
D3[V1]= 7
D3[V5]=
infinito
D3[V6]= 6
V*3=6
3 V3=[v2,v3,v4,v3*]
V3*= V6
D3[V3*]= 6
D3[V1]= 7
D3[V1]=
infinito
D3[V1]=
infinito
D3[V5]= 10
V*5=V1
4 V4=[v2,v3,v4,v6,vl] V*4= V5
D3[V4*]= 10
D3[V1*=
infinito
D4[v1]=13 V*5=V1