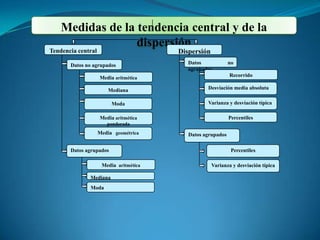
Este documento presenta información sobre tablas de frecuencia y medidas estadísticas. Explica que una tabla de frecuencia ordena y cuenta la frecuencia de datos estadísticos. Luego describe cómo calcular medidas como la media, mediana y moda para datos agrupados y no agrupados, así como medidas de dispersión como rango, desviación media, varianza y desviación típica.

1. INTEGRANTES:
ESPINOZA YACOLCA KATHERINE
AROCUTIPA APOMAYTA MARIA ELENA
ALVARADO CORDOVA MAGALY

2. La distribución de frecuencias o tabla de frecuencias
es una ordenación en forma de tabla de los datos
estadísticos, asignado a cada dato su frecuencia
correspondiente.

3.  Una vez obtenidos los datos como producto de la
aplicación de un instrumento de medición estos se
codifican y se almacenan en una matriz de datos.

4.  Tablas de frecuencia.- son el resumen del
comportamiento de una sola variable.
 Tablas de contingencia.- muestran el comportamiento
de dos o más variables.

5. Tablas de frecuencia para
variable categórica
Presentación de variables
numéricos
VARIABLE FRECUENCIA
Categ. 1
Categ. 2
Categ. N
F1
F2
FK
Total N
NOTAS N° DE
ALUMNOS
13-14
15-16
17-18
20
40
20
Total 80

6. Variable fi hi FI HI
Catg. 1 f1 h1 F1 H1
Catg. 2 f2 h2 F2 H2
. . . . .
. . . . .
. . . . .
Catg. K Fk hk Fk Hk
Total N 1
Donde:
fi: Es la frecuencia observada (frecuencia absoluta). Indica el número de veces que
se repite el dato.
hi: Es la frecuencia relativa. Indica la proporción de veces que se presenta un dato.
hi=fi/N
FI: Es la frecuencia absoluta acumulada.
FI=f1
F2=f1+f2
F3=f1+f2+f3
HI: Es la frecuencia relativa acumulada
H1=h1
H2=h1
H3=h1+h2+h3

7. En la siguiente encuesta se da a conocer las
calificaciones de 35 alumnos de primer año de la
asignatura de matemática del IE. "San Martín"
12; 14; 20; 15; 10; 11; 15; 18; 13; 19; 11; 20; 09;
16; 15; 12; 14; 16; 10; 18; 12; 13; 12; 14; 11; 14;
12; 11; 14; 16; 18; 10; 17; 17; 14.
Construya tabla de frecuencia sin agrupar

8. .
b. ¿Cuál es la frecuencia relativa del grupo que obtuvo nota 11?
Rpta. 0.11
c. ¿Cuántos obtuvieron nota 18?
Rpta. 03 alumnos
d. ¿Cuántos alumnos obtuvieron nota mayor a 16?
Rpta. 11 alumnos
e. ¿Cuántos alumnos obtuvieron notas menores que 13?
Rpta. 13 alumnos
f. ¿Cuántos alumnos están desaprobados?
Rpta. 04 alumnos

10.  Límites de la clase
Cada clase está delimitada por el límite inferior de la clase y
el límite superior de la clase.
 Amplitud de la clase
La amplitud de la clase es la diferencia entre el límite
superior e inferior de la clase.
 Marca de clase
La marca de clase es el punto medio de cada intervalo y es
el valor que representa a todo el intervalo para el cálculo de
algunos parámetros

11. 10 15 11 8 12 10 13 10 12 10
12 17 10 12 11 14 15 20 10 12
10 20 14 13 6 16 6 6 14 18
7 5 12 11 2 4 14 18 16 17
Notas fi
2 1
4 1
5 1
6 3
7 1
8 1
10 7
11 3
12 6
13 2
14 4
15 2
16 2
17 2
18 2
20 2
TOTAL 40

12. 1.- Calcular el rango:
R= Dato mayor - dato menor
R=20-2 = 18
2.- Determinar la cantidad de intervalos
K= 1 + 3.33 *logN
K= 1+3.33*log(40)
K= 6
3.- Determinación de la amplitud de los intervalos:
Amplitud= Rango/n° de intervalos
= 18/6= 3
4.- Finalizamos con construir la tabla de datos agrupados
con la información.

13. Rango 18
Intervalo 6
Amplitud 3
INTERVALOS fi hi FI HI
Marca de
clase
2 5 2 0.05 2 0.05 3.5
5 8 5 0.125 7 0.175 6.5
8 11 8 0.2 15 0.375 9.5
11 14 11 0.275 26 0.65 12.5
14 17 8 0.2 34 0.85 15.5
17 20 6 0.15 40 1 18.5
40 1

14. Medidas de la tendencia central y de la
dispersión
Tendencia central Dispersión
Datos no
agrupados
Recorrido
Desviación media absoluta
Varianza y desviación típica
Percentiles
Datos agrupados
Percentiles
Varianza y desviación típica
Datos no agrupados
Media aritmética
Mediana
Moda
Media aritmética
ponderada
Media geométrica
Datos agrupados
Media aritmética
Mediana
Moda

15. Medidas de la tendencia central y de la
dispersión
Las medidas de tendencia central tienen como objetivo el
sintetizar los datos en un valor representativo, las medidas de
dispersión nos dicen hasta que punto estas medidas de
tendencia central son representativas como síntesis de la
información. Las medidas de dispersión cuantifican la
separación, la dispersión, la variabilidad de los valores de la
distribución respecto al valor central. Distinguimos entre
medidas de dispersión absolutas, que no son comparables
entre diferentes muestras y las relativas que nos permitirán
comparar varias muestras.

17. MEDIA ARITMETICA
Ejemplo
Los pesos de seis
amigos son: 84, 91,
72, 68, 87 y 78 kg.
Hallar el peso
medio.
Es el valor resultante
que se obtiene al
dividir la sumatoria
de un conjunto de
datos sobre el
número total de
datos. Solo es
aplicable para el
tratamiento de datos
cuantitativos.

18. MEDIANA
Ejemplo:
Encontrar la mediana para los
siguientes datos:
4 1 2 3 4 2 2 1 5 5 3
SOLUCIÓN
1: Ordenar los datos.
1 1 2 2 2 3 3 4 4 5 5
2: Localizar el valor que divide en
dos parte iguales el número de datos.
1 1 2 2 2 3 3 4 4 5 5
La mediana es 3, dejando 5 datos a
cada lado.
Mediana (Me):
Valor que divide
una serie de datos
en dos partes
iguales. La cantidad
de datos que queda
por debajo y por
arriba de la mediana
son iguales.

19. MODA
ejemplo: “hallar la
moda del siguiente
conjunto de datos.”
14,15,16,18,5,7,5,9,15,
5.
se ordenan:
5,5,5,7,9,14,15,15,16,1
8.
la moda es igual a 5..
La moda es el valor que
se presenta con mayor
frecuencia en un conjunto
de datos. a una
distribución que tiene una
sola moda se le denomina
unimodal, si tiene dos
datos que se repiten
igualmente, se le conoce
como bimodal, y si tiene
tres o mas modas se le
conoce como multimodal.
si ningún dato se repite,
entonces no tiene moda.

20. MEDIAARITMETICA PONDERADA
Tiene en cuenta la
importancia relativa de las
observaciones, es superior a
la media aritmética simple

21. MEDIA GOMETRICA
Por ejemplo, la media
geométrica de 2 y 18 es
En matemáticas y
estadística, la media
geométrica de una
cantidad arbitraria de
números (digamos n
números) es la raíz n-
ésima del producto
de todos los
números.

22. DATOS AGRUPADOS
En la mayor parte de casos tenemos un
número grande de datos y tomamos en
cuenta que en estos casos generalmente
los datos son resumidos en una tabla de
frecuencia. La fórmula para el cálculo
cuando se trata de datos agrupados es
diferente a la de los no agrupados.

23. MEDIA ARITMETICA
Si los datos vienen
agrupados en una
tabla de frecuencias, la
expresión de la media
es:
La media
aritmética es igual
a la división de la
sumatoria del
producto de las
clases por la
frecuencia sobre el
número de datos.

24. MEDIANA
EJEMPLO
Las calificaciones en la asignatura
de Matemáticas de 39 alumnos de
una clase viene dada por la
siguiente tabla:
Calificaciones 1 2 3 4 5 6 7 8 9
Número de alumnos 2 2 4 5 8 9 3 4
2
Se halla las frecuencias absolutas
acumuladas .Asociada a la
mediana para n impar, se obtiene .
Ni-1< n/2 < Ni = N19 < 19.5 < N20
Me = 5 puntos, la mitad de la clase
ha obtenido un 5 o menos, y la otra
mitad un 5 o más.
En el ámbito de
la estadística,
una mediana es
el valor de la
variable que deja
el mismo número
de datos antes y
después que él,
una vez
ordenados estos.

25. Se llaman medidas de dispersión aquellas que
permiten retratar la distancia de los valores de la
variable a un cierto valor central, o que permiten
identificar la concentración de los datos en un cierto
sector del recorrido de la variable. Se trata de
coeficiente para variables cuantitativas.
Las medidas de dispersión mas usados son:
Rango
Desviación media
Varianza
Desviación típica
Coeficiente de desviación

26. El rango es la diferencia entre el mayor y el menor de
los datos de una distribución estadística.
En {24, 18,10, 9, 36, 20, 41}
el menor valor es 9, y el mayor es 41, entonces el
rango es
41 – 9 = 32

27. La desviación media es la media aritmética de los
valores absolutos de las desviaciones respecto a la
media.
La desviación media se representa por
Ejemplo:
Calcular la desviación media de la distribución
9, 3, 8, 8, 9, 8, 9, 18

28. Si los datos vienen agrupados en una tabla de frecuencias, la
expresión de la desviación media es.
Calcular la desviación media de la distribución:
xi fi xi · fi |x - x| |x - x| · fi
[10, 15) 12.5 3 38 9.286 27.858
[15, 20) 17.5 5 88 4.286 21.43
[20, 25) 22.5 7 158 0.714 4.998
[25, 30) 27.5 4 110 5.714 22.856
[30, 35) 32.5 2 65 10.174 21.428
21 458 98.57

29. La varianza es la media aritmética del cuadrado de las
desviaciones respecto a la media de una distribución
estadística.
Varianza para datos agrupados
xi fi xi · fi xi
2
· fi
[10, 20) 15 1 15 225
[20, 30) 25 8 200 5000
[30,40) 35 10 350 12 250
[40, 50) 45 9 405 18 225
[50, 60 55 8 440 24 200
[60,70) 65 4 260 16 900
[70, 80) 75 2 150 11 250
42 1 820 88 050

30. La desviación típica es la raíz cuadrada de la varianza.
Es decir, la raíz cuadrada de la media de los cuadrados de
las puntuaciones de desviación
xi fi xi · fi xi
2
· fi
[10, 20) 15 1 15 225
[20, 30) 25 8 200 5000
[30,40) 35 10 350 12 250
[40, 50) 45 9 405 18 225
[50, 60 55 8 440 24 200
[60,70) 65 4 260 16 900
[70, 80) 75 2 150 11 250
42 1 820 88 050

31. Es un estadístico de dispersión que tiene la ventaja de que no lleva
asociada ninguna unidad, por lo que nos permitirá decir entre dos
muestras, cual es la que presenta mayor dispersión. La denotaremos por
c.v.
xi fi xi · fi xi
2
· fi
[10, 20) 15 1 15 225
[20, 30) 25 8 200 5000
[30,40) 35 10 350 12 250
[40, 50) 45 9 405 18 225
[50, 60 55 8 440 24 200
[60,70) 65 4 260 16 900
[70, 80) 75 2 150 11 250
42 1 820 88 050
C.V=
14.797
* 100
43.33
C.V = 34%