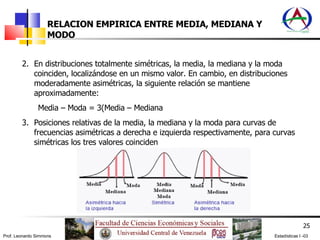
El documento explica las tres principales medidas de tendencia central: la media aritmética, la mediana y la moda. Define cada una y describe cómo se calculan para datos agrupados y no agrupados. Explica que la media es el valor alrededor del cual se agrupan los datos, la mediana divide la distribución en dos partes iguales, y la moda es el valor más frecuente. Además, compara sus propiedades y cuándo es más adecuada cada medida.

1. UCV/FACES/EAC Estadísticas I Medidas de Tendencia Central Prof. Leonardo Simmons

2. MEDIDAS DE TENDENCIA CENTRAL Las características globales de una población o muestra de una variable cuantitativa pueden resumirse mediante una serie de cantidades numéricas representativas llamadas parámetros o estadísticos, según sea el caso de una población o una muestra. Entre ellas, las medidas de tendencia central, como la media aritmética, la moda o la mediana, ayudan a conocer de forma aproximada el comportamiento de una distribución estadística. Se llama medidas de tendencia central o centralización a unos valores numéricos en torno a los cuales se agrupan, en mayor o menor medida, los valores de una variable estadística. Las tres medidas más usuales de tendencia central son: La media Aritmética La Mediana El Modo o Moda

3. Las medidas de tendencia central son parámetros o estadísticos representativos de distribuciones de frecuencia como las que ilustra la imagen. MEDIDAS DE TENDENCIA CENTRAL

4. MEDIA ARITMETICA Media Aritmética : Se define como el “centro de gravedad” de la distribución estadística de una variable. Sea X una variable cuantitativa donde X 1 , X 2 , ….. X k ; y f 1 , f 2 ,….. f k son sus respectivos valores y frecuencias, entonces a la media aritmética de X la denotaremos por si se trata de una muestra ó µ x si analizamos la población, luego:

5. CALCULO DE LA MEDIA ARITMETICA Caso de una Distribución de Frecuencia de Datos No Agrupados (DFDNA): P.ej: Un pediatra obtuvo la siguiente tabla sobre los meses de edad de 50 niños de su consulta en el momento de andar por primera vez: Luego: Ubicación de la Media Aritmética 12,2

6. CALCULO DE LA MEDIA ARITMETICA Caso de una Distribución de Frecuencia de Datos Agrupados: P.ej: Las alturas de los jugadores de un equipo de baloncesto vienen dadas por la tabla: Luego: 172,5 177,5 182,5 187,5 192,5 197,5 1 3 2 5 4 6 8 7 No. Jugadores Estatura (cms)

7. PROPIEDADES DE LA MEDIA ARITMETICA 1 . La suma de las diferencias de la variable con respecto a la media es nula, es decir: 2 . La suma de los desvíos de los valores de una variable respecto a la media aritmética de estos es un mínimo, es decir: 3 . Si sumamos o restamos una constante a todos los valores de una variable manteniendo fijas las frecuencias entonces la media de la nueva variable así generada será igual a la media de la variable origina más o menos la constante, según sea el caso:

8. PROPIEDADES DE LA MEDIA ARITMETICA Sean X 1 , X 2 , ….. X k y f 1 , f 2 ,….. f k los valores de la variable X y sus respectivas frecuencias y cuya media es , entonces si sumamos o restamos una constante C a cada valor de X para así generar la variable Y , es decir: Y 1 = X 1 ± C ; Y 2 = X 2 ± C ; ……Y k ,=X k ± C, manteniendo Y las mismas frecuencias que X entonces: 4 . Si multiplicamos o dividimos por una constante a todos los valores de una variable manteniendo fijas las frecuencias entonces la media de la nueva variable así generada será igual a la media de la variable original multiplicada o dividida por la constante, según sea el caso:

9. PROPIEDADES DE LA MEDIA ARITMETICA 5. La media aritmética es un operador lineal, es decir: Si Y = a X + b; donde a, b son constantes entonces: 6. Dados r muestras de la misma variable cada una de tamaño n 1 , n 2 , ..., n r observaciones y siendo , , ..., las respectivas medias de cada uno de ellas; entonces la media aritmética de la unión de todas las muestras es: A la expresión demarcada se le conoce como media ponderada

10. PROPIEDADES DE LA MEDIA ARITMETICA 7. Dados r muestras de la misma variable cada una de igual tamaño n observaciones y siendo , , ..., las respectivas medias de cada uno de ellas; entonces la media aritmética de la unión de todas las muestras es: Es la media simple de las medias de las muestras

11. OBSERVACIONES SOBRE LA MEDIA ARITMETICA La media se puede hallar sólo para variables cuantitativas La media es independiente de las amplitudes de los intervalos de una DFDA La media es muy sensible a las puntuaciones extremas. P.ej. Si tenemos una distribución con los siguientes pesos: 65 kg, 69kg , 65 kg, 72 kg, 66 kg, 75 kg, 70 kg, 110 kg. La media es igual a 74 kg, que es una medida de centralización poco representativa de la distribución La media no se puede calcular en una DFDA si hay un intervalo o clase con una amplitud indeterminada, es decir, de rango abierto La media es un estadístico “suficiente” porque usa toda la información de la muestra Valores Extremos La Media pierde Representatividad

12. MEDIANA Mediana Se define como el valor de la variable que divide la distribución en dos parte iguales del 50%, es decir, el 50% de los datos es menor o igual a él y el restante 50% el mayor o igual a él. Se denota M e El 50% de los primeros datos de la distribución son ≤ Me El restante 50% de los datos de distribución son ≥ Me M e

13. CALCULO DE LA MEDIANA Caso de una Distribución de Frecuencia de Datos No Agrupados (DFDNA): P.ej: Caso del pediatra Procedimiento: Calcular n/2 Si F j tal que F j = n/2 M e = X j de lo contrario, M e será aquel valor de X cuya frecuencia acumulada sea mayor inmediato a n/2 En este caso n/2 = 50/2 =25 y como no existe una frecuencia acumulada igual a 25 y la frecuencia acumulada mayor inmediata a n/2 es 30 entonces: M e = X 4 = 12 meses Vemos que efectivamente hay 25 (50%) valores ≤ a 12 y 25 (50% ≥ a 12

14. CALCULO DE LA MEDIANA Si organizamos la serie de datos anterior denotando la posición que ocupa cada observación tenemos: X 9, 10, 10, 10, 10, 11, 11, 11, ….. 11, 12, 12,…… 12, 12,……50 Posición: 1ª, 2ª, 3ª, 4ª, 5ª, 6ª, 7ª, 8ª,……,14ª, 15ª,16ª,…… 25ª ,26ª,..50ª 9 10 11 12 13 14 15 2 6 4 10 8 12 16 14 No.Niños M e Meses

15. Procedimiento: Calcular n/2 Si F j tal que F j = n/2 M e = L me , donde L me es el limite superior de la clase correspondiente a la F j = n/2; de lo contrario: CALCULO DE LA MEDIANA Caso de una Distribución de Frecuencia de Datos Agrupados (DFDA): P.ej: Caso de la estatura de los jugadores de baloncesto

16. CALCULO DE LA MEDIANA Donde: l me = limite inferior de clase que contiene a la M e F me-1 = Frecuencia acumulada hasta la clase inmediata anterior a la clase que contiene a la M e f me = la frecuencia de la clase que contiene a la M e ; y C me = El rango de la clase que contiene a la M e Nota: La clase o intervalo que contiene a la M e es aquella correspondiente a la frecuencia acumulada inmediata mayor a n/2

17. CALCULO DE LA MEDIANA En el ejemplo: n/2 = 23/2 = 11,5 luego no existe frecuencia acumulada igual a n/2 por lo tanto buscamos la frecuencia acumulada inmediata superior a N/2 que resulta la F 4 = 16, luego la clase que contiene a la Me es la cuarta clase entonces: 172,5 177,5 182,5 187,5 192,5 197,5 1 3 2 5 4 6 8 7 No. Jugadores Estatura (cms)

18. CALCULO DE LA MEDIANA Analizando trigonométricamente los triangulas rectángulos ABC y ADE se genera la formula de interpolación de la Mediana: l 1 L 1 L 2 ………. L me-1 L me …………… F 1 F 2 F me-1 F me : : : : n n/2 M e A B C E D

19. OBSERVACIONES ACERCA DE LA MEDIANA La mediana no esta influenciada por los valores extremos ya que su determinación se apoya en los valores centrales de la variable Su uso es apropiado ante distribuciones asimétricas No es un estadístico “suficiente” ya que no aprovecha toda la información de la muestra Valores Extremos La Media pierde Representatividad M e

20. MODO o MODA Modo o Moda Se define como el valor de la variable que más se repite, es decir, el valor de la variable que tenga frecuencia máxima. Se denota con M o M o = X j si y solo si f j = Max { f i , i=1, 2, 3,…..k} Hablaremos de una distribución bimodal de los datos, cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es en la que encontramos tres modas. Si todas las variables tienen la misma frecuencia diremos que no hay moda.

21. CALCULO DEL MODO Caso de una Distribución de Frecuencia de Datos No Agrupados (DFDNA): P.ej: Caso del pediatra Procedimiento: Determinar la frecuencia máxima, f max , el modo será igual al valor de la variable asociado a dicha frecuencia. En este caso f max = 16 por lo tanto: M o = 12 meses

22. CALCULO DEL MODO Caso de una Distribución de Frecuencia de Datos No Agrupados (DFDA): P.ej: Caso de los jugadores Procedimiento: Determinar la frecuencia máxima, f max , el modo estará ubicado en la clase correspondiente a dicha frecuencia máxima y entonces: Donde: f mo = frecuencia de la clase que contiene al M o f mo-1 = frecuencia de la clase anterior a la que contiene al M o f mo-1 = frecuencia de la clase siguiente a la que contiene al M o

23. CALCULO DEL MODO En nuestro ejemplo: f mo = 8; luego X = 186,63 cms M e = 187,18 cms M o = 187, 86 172,5 177,5 182,5 187,5 192,5 197,5 1 3 2 5 4 6 8 7 No. Jugadores Estatura (cms)

24. OBSERVACIONES ACERCA DEL MODO La moda se puede determinar en todos los tipos de mediciones (nominal, ordinal, de intervalos, y relativa). La moda tiene la ventaja de no ser afectada por valores extremos. Al igual que la mediana, puede ser calculada en distribuciones con intervalos abiertos. En muchas series de datos no hay moda porque ningún valor aparece más de una vez. En algunas series de datos hay más de una moda, en este caso uno podría preguntarse ¿cual es el valor representativo de la serie de datos?

25. RELACION EMPIRICA ENTRE MEDIA, MEDIANA Y MODO En distribuciones totalmente simétricas, la media, la mediana y la moda coinciden, localizándose en un mismo valor. En cambio, en distribuciones moderadamente asimétricas, la siguiente relación se mantiene aproximadamente: Media – Moda = 3(Media – Mediana Posiciones relativas de la media, la mediana y la moda para curvas de frecuencias asimétricas a derecha e izquierda respectivamente, para curvas simétricas los tres valores coinciden

26. TAREA No. 3 Resolver del libro Estadística para Administración y Economía – Anderson – 8va. Edición , capitulo 3, los ejercicios del 5 al 14 (pag. 79 al 83) Investigue acerca de estas otras medias Armónica y Geométrica: definición, calculo, aplicaciones y propiedades. La relación existente entre la media aritmética, la armónica y la geométrica Investigue en internet algunas medidas de tendencia de la economía venezolana