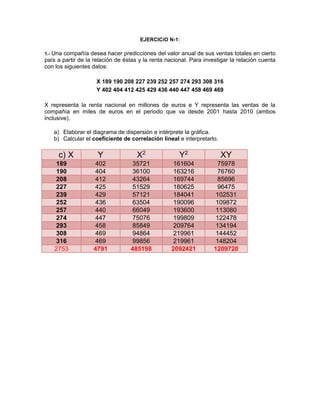
El documento presenta los resultados de tres ejercicios estadísticos realizados para calcular el coeficiente de correlación lineal entre diferentes variables. En el primer ejercicio, se calcula la correlación entre la renta nacional y las ventas de una compañía, obteniendo un coeficiente positivo pero no muy fuerte. En el segundo ejercicio, la correlación entre años de experiencia y número de infracciones de conductores es negativa y fuerte. En el tercer ejercicio, al graficar la relación entre metros cuadrados y ingresos de tiendas, la correlación lineal result

1. República Bolivariana de Venezuela
Ministerio Del Poder Popular Para la Educación
Instituto Universitario de Tecnología
“Antonio José De Sucre”
Barquisimeto-Edo Lara
Integrante:
Nayibe Mendoza
C.I:18.430.020

2. EJERCICiO N-1:
1.- Una compañía desea hacer predicciones del valor anual de sus ventas totales en cierto
país a partir de la relación de éstas y la renta nacional. Para investigar la relación cuenta
con los siguientes datos:
X 189 190 208 227 239 252 257 274 293 308 316
Y 402 404 412 425 429 436 440 447 458 469 469
X representa la renta nacional en millones de euros e Y representa las ventas de la
compañía en miles de euros en el periodo que va desde 2001 hasta 2010 (ambos
inclusive).
a) Elaborar el diagrama de dispersión e intérprete la gráfica.
b) Calcular el coeficiente de correlación lineal e interpretarlo.
c) X Y X2
Y2
XY
189 402 35721 161604 75978
190 404 36100 163216 76760
208 412 43264 169744 85696
227 425 51529 180625 96475
239 429 57121 184041 102531
252 436 63504 190096 109872
257 440 66049 193600 113080
274 447 75076 199809 122478
293 458 85849 209764 134194
308 469 94864 219961 144452
316 469 99856 219961 148204
2753 4791 485198 2092421 1209720

3. B.- COEFICIENTE DE CORRELACION LINEAL
𝑥̅=
2753
11
= 250,27
𝒚̅= 𝟒𝟕𝟗𝟏
𝟏𝟏 = 435,54
Sx= √485198 − 250,27
2
= √43858,63
11
Sx= 209,42
Sy= √2092421 − (435,54)2
= √524,99
11
Sy= 22,91
390
400
410
420
430
440
450
460
470
480
490
0 50 100 150 200 250 300 350
diagramade dispersion
diagrama de dispersion

4. Por definición de la formula se tiene:
rxy= 1209720 - (250,27) (435,54)
11
(209,42) (22,91)
rxy = 971,94 = 0,2025
4797,8122
El coeficiente de correlación lineal es:
r = rxy
sxsy
r= 0,2025
(209,42) (22,91)
r= 4,22X10-5
El Coeficiente De Correlación Lineal Es Positivo, La Correlación Es Directa Y No Es Muy
Fuerte Ya Que Esta Alejado Del 1
EJERCICIO N-2:
2.-En una empresa de transportes trabajan cuatro conductores. Los años de antigüedad de
permisos de conducir y el número de infracciones cometidas en el último año por cada uno de ellos
son los siguientes:
Años (X) 3 4 5 6
Infracciones (Y) 4 3 2 1
a) Calcular el coeficiente de correlación lineal e interpretarlo.
𝑋̅ =
18
4
= 4,5
X Y X2
Y2
XY
3 4 9 16 12
4 3 16 9 12
5 2 25 4 10
6 1 36 1 6
18 10 86 30 40

5. 𝑌̅ =
10
4
= 2,5
Sx= √
86
4
(4,5)
2
= √1,25
Sx= 1,11
Sy= √30
4
- (2,5)2 =
√1,25
Sy= 1,11
rxy=
40
4
− (4,5)(2,5)
(1,11)(1,11)
rxy = −1,25
1,23
rxy= -1,014
LA CORRELACION ES INVERSA POR LO TANTO ES:
r = rxy
sxsy
r = 1,014
(1,11)2
r= -0,822
La correlación es fuerte e inversa
EJERCICIO N-3:
Una compañía que tiene 15 tiendas ha recopilado datos en relación con los metros cuadrados de
área de ventas respecto a los ingresos mensuales. Trace una gráfica de los datos, y si le parece
apropiado determine la correlación.
Tienda Metros 2 Ingreso
X Y
a 55 45
o 80 60
j 85 75
e 90 75
k 90 80

6. d 110 95
n 130 95
g 140 110
c 180 120
l 180 105
b 200 115
i 200 130
h 215 140
f 260 170
m 300 200
15 2315 1615
X Y X2
Y2
XY
55 45 3025 2025 2475
80 60 6400 3600 4800
55 80 85 90 90 110 130 140 180 180 200 200 215 260 300
200
170
140
130
120
115
110
105
95
95
80
75
60
45
170
140
130
120
115
110
105
95
95
80
75
60
45
130
120
115
110
105
95
95
80
75
60
45
140
130
120
115
110
105
95
95
80
75
60
45
115
110
105
95
95
80
75
60
45
120
115
110
105
95
95
80
75
60
45
75
60
45
80
75
60
45
95
80
75
60
45
95
95
80
75
60
45
105
95
95
80
75
60
45
110
105
95
95
80
75
60
45
45
60
45
75
60
45
INGRESO
METROS

7. 85 75 7225 5625 6375
90 75 8100 5625 6750
90 80 8100 6400 7200
110 95 12100 9025 10450
130 95 16900 9025 12350
140 95 16900 9025 12350
180 120 32400 14400 21600
180 105 32400 11025 18900
200 115 40000 13225 23000
200 130 40000 16900 26000
215 140 46225 19600 30100
260 170 67600 28900 44200
300 200 90000 40000 60000
2315 1615 430075 191850 289600
Coeficiente de Correlación Lineal:
𝑋 = 𝑁
∑ 𝑋
=
2315
15
= 154,33
𝑌 = 𝑁
∑ 𝑌
=
1615
15
= 107,66
𝑆𝑋 = √
∑ 𝑋
2
𝑁
− 𝑋2
= √
430075
15
− (154,33)2
=
𝑆𝑋 = √4853,91 =
𝑆𝑋 = 69.67
𝑆𝑌 = √
∑ 𝑌
2
𝑁
+ 𝑌2 =
𝑆𝑌 = √
141850
15
− (107,66)2
=
𝑆𝑌 = √1199,32 =
𝑆𝑌 = 34,63
𝑟 𝑥𝑦 =
∑ 𝑥𝑦
𝑁
− 𝑋 𝑌
5 ∗ 54
=

8. 𝑟 𝑥𝑦 =
289600
15
− (154,33). (107,66)
(69,67). (34,63)
=
𝑟 𝑥𝑦 =
2691,49
2412,67
=
𝑟 𝑥𝑦 = 1,115
𝑟 =
𝑟 𝑥𝑦
5 ∗ 54
=
𝑟 =
1,115
(69,67). (34,63)
=
𝑟 = 4,621𝑥10−4
La correlación lineal es positiva.