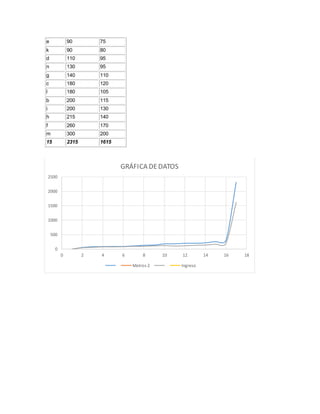
El documento presenta tres ejercicios estadísticos que deben ser resueltos por un estudiante para una asignatura de Estadística General. El primer ejercicio pide graficar y analizar la correlación entre la renta nacional y las ventas de una compañía de 2001 a 2010. El segundo ejercicio calcula la correlación entre los años de experiencia de conductores y las infracciones cometidas. Y el tercer ejercicio grafica los metros cuadrados y los ingresos de 15 tiendas para determinar su posible correlación.

1. INSTITUTO UNIVERSITARIO DE TECNOLOGÍA
“ANTONIO JOSÉ DE SUCRE”
NÚCLEO LARA
ESTADÍSTICA GENERAL
PARTICIPANTE: Arlet Zambrano
C.I. N° V-22.189.587
AGOSTO - 2014

2. Después de leer el material presentado, resuelva los ejercicios que a continuación se
plantean: Ejercicios. Fecha tope de entrega el 27/08/2014. Ponderación: 15%. Debe realizarlo en
slideshare y enviar la URL por el foro que se llamará resolución de los ejercicios.
1.- Una compañía desea hacer predicciones del valor anual de sus ventas totales en cierto país a
partir de la relación de éstas y la renta nacional. Para investigar la relación cuenta con los siguientes
datos:
X 189 190 208 227 239 252 257 274 293 308 316
Y 402 404 412 425 429 436 440 447 458 469 469
X representa la renta nacional en millones de euros e Y representa las ventas de la compañía en
miles de euros en el periodo que va desde 2001 hasta 2010 (ambos inclusive).
a) Elaborar el diagrama de dispersión e intérprete la gráfica.
900
800
700
600
500
400
300
200
100
Diagrama de Dispersión
INTERPRETACIÓN: en términos estadísticos se evidencias una correlación o comportamiento
equivalente entre la renta nacional en millones de euros y las ventas de la compañía en miles de
euros en el período 2001 – 2009, a pesar que X es a nivel nacional y el Y de una compañía,
b) Calcular el coeficiente de correlación lineal e interpretarlo.
2 Yi
Xi yi Xi,Yi Xi
2
189 402 75.978 35.721 161.604
190 404 76.760 36.100 163.216
208 412 85.696 43.264 169.744
227 425 96.475 51.529 180.625
239 429 102.531 57.121 184.041
252 436 109.872 63.504 190.096
257 440 113.080 66.049 193.600
274 447 122.478 75.076 199.809
0
1 2 3 4 5 6 7 8 9 10 11
X Y

3. 293 458 134.194 85.849 209.764
308 469 144.452 94.864 219.961
316 469 148.204 99.856 219.961
2.756 4.788 1.209.720 708.663 2.092.421
MEDIA Xi= 2.756 / 11 = 250,5 y = 4.788 / 11 = 435,3
DESVIACIÓN TÍPICA
휎푥 = √708.663/11 − (250,5)2 = 40,9
휎푦 = √2.092.421/11 − (453 ,3)2 = 27,1
COVARIANZA
휎푥푦 =
1.209.720
11
− 250,5 ∗ 435,3 = 931,9
r = 931,9
40,9∗27,1
= 0,8
INTERPRECIÓN: Para este caso la correlación es directa y positiva como se
evidencia en el resultado obtenido
2.- En una empresa de transportes trabajan cuatro conductores. Los años de
antigüedad de permisos de conducir y el número de infracciones cometidas en el
último año por cada uno de ellos son los siguientes:
Años (X) 3 4 5 6
Infracciones (Y) 4 3 2 1

4. a) Calcular el coeficiente de correlación lineal e interpretarlo.
2 Yi
X Y Xi
2 Xi.Yi
03 04 09 16 12
04 03 16 09 12
05 02 25 04 10
06 01 36 01 06
18 10 86 30 40
MEDIA
Xi = 18/4 = 4,5 Yi = 10/4 = 2,5
DESVIACIÓN
휎푥 = √86/4 − (4,5)2 = 1,1
휎푦 = √30/4 − (2,5)2 = 1,1
COVARIANZA
휎푥푦 =
40
4
− 4,5 ∗ 2,5 = - 1,3
r = − 1,3
1,1∗1,1
= −1,2
INTERPRETACIÓN: correlación es negativo, lo que indica que es inversa.
3.- Una compañía que tiene 15 tiendas ha recopilado datos en relación con los
metros cuadrados de área de ventas respecto a los ingresos mensuales. Trace una
gráfica de los datos, y si le parece apropiado determine la correlación.
Tienda Metros 2 Ingreso
X Y
a 55 45
o 80 60
j 85 75

5. e 90 75
k 90 80
d 110 95
n 130 95
g 140 110
c 180 120
l 180 105
b 200 115
i 200 130
h 215 140
f 260 170
m 300 200
15 2315 1615
2500
2000
1500
1000
500
0
GRÁFICA DE DATOS
0 2 4 6 8 10 12 14 16 18
Metros 2 Ingreso