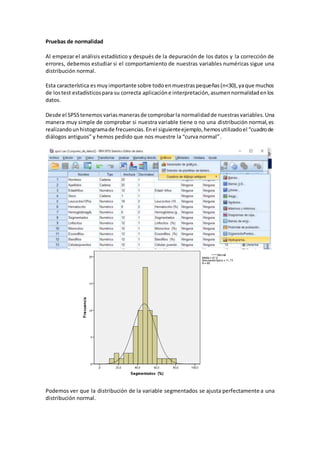
Para comprobar si las variables numéricas siguen una distribución normal, es importante realizar pruebas de normalidad, especialmente en muestras pequeñas. Se pueden usar histogramas y la prueba de Kolmogorov-Smirnov para evaluar la normalidad. La prueba de Kolmogorov-Smirnov contrasta si una variable sigue una distribución normal (hipótesis nula) u otra distribución (hipótesis alternativa), y se acepta la hipótesis nula si el valor p es mayor a 0.05.

1. Pruebas de normalidad
Al empezar el análisis estadístico y después de la depuración de los datos y la corrección de
errores, debemos estudiar si el comportamiento de nuestras variables numéricas sigue una
distribución normal.
Esta característica esmuy importante sobre todoenmuestraspequeñas(n<30),yaque muchos
de lostest estadísticospara su correcta aplicacióne interpretación,asumennormalidadenlos
datos.
Desde el SPSStenemosvariasmanerasde comprobarla normalidadde nuestrasvariables.Una
manera muy simple de comprobar si nuestra variable tiene o no una distribución normal,es
realizandounhistogramade frecuencias.Enel siguienteejemplo,hemosutilizadoel “cuadrode
diálogos antiguos” y hemos pedido que nos muestre la “curva normal”.
Podemos ver que la distribución de la variable segmentados se ajusta perfectamente a una
distribución normal.

2. En este otroejemplo,lavariablehematocrito,nosigue unadistribuciónnormal,yaque muestra
una acusada asimetría hacia la derecha.
Una de las pruebas estadísticas más conocidas que valora la Normalidad, es la prueba de
Kolmogorov-Smirnov:
Analizar Þ Pruebas no paramétricas Þ K-S de 1 muestra…

3. En el cuadro de diálogose seleccionarálavariable a analizary su distribución(en nuestrocaso
normal).Enla pestañaOpcionesse puedensolicitarlosestadísticosdescriptivosyloscuartiles.
Hipótesis que se contrasta con la prueba de Kolmogorov-Smirnov:
 H0: La variable sigue una distribución normal (hipótesis nula).
 H1: La variable no sigue una distribución normal (hipótesis alternativa).

4. El valor de p está en “Sig. Asintót. (bilateral)” en nuestro caso p=0.219
Como la p es mayor de 0.05, no podemosrechazarla hipótesisnula,por loque asumimosque
nuestra variable sigue una distribución normal