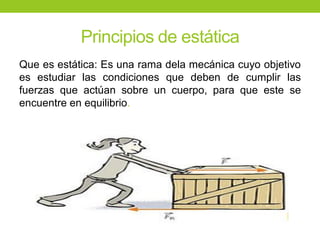
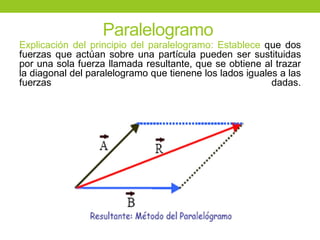
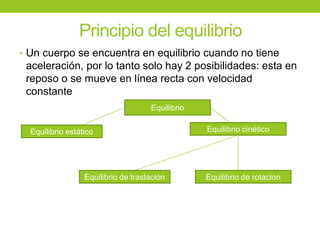
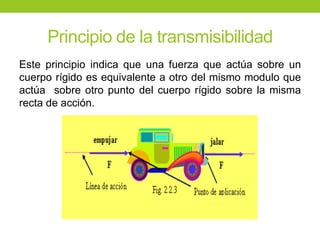
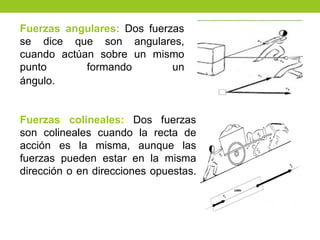
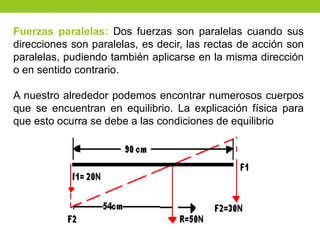
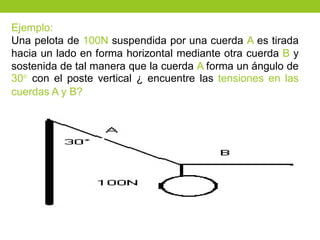
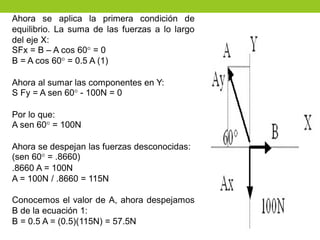
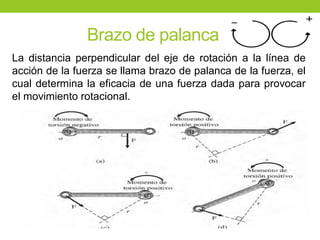
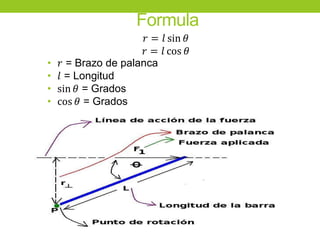
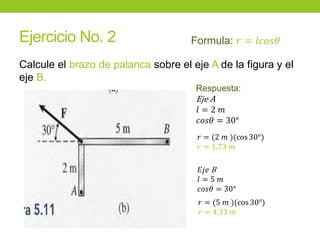
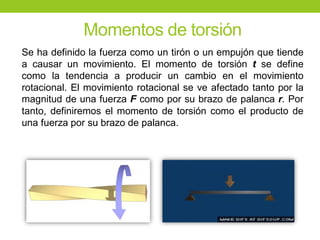
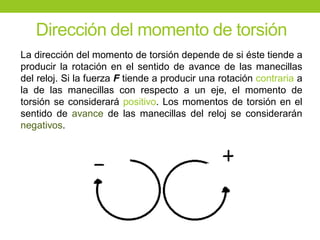
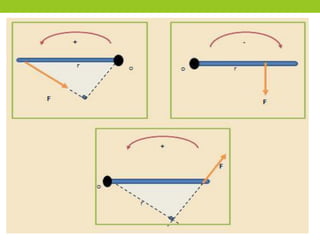
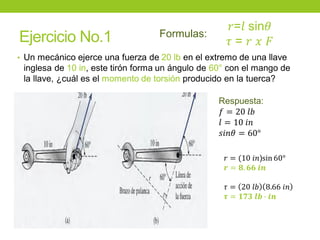
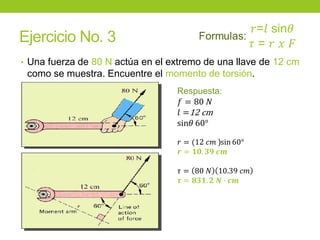
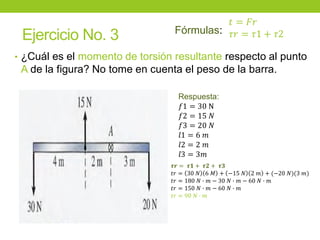
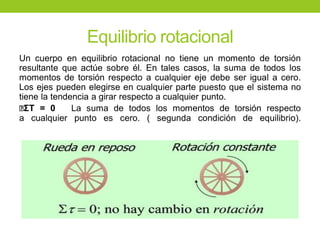
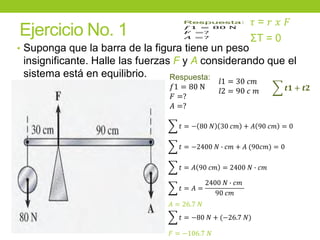
Este documento describe los principios básicos de la estática, incluyendo el equilibrio de fuerzas, paralelogramo de fuerzas, y momentos de torsión. Explica las condiciones de equilibrio para cuerpos en reposo o movimiento constante, así como cómo calcular la resultante y brazo de palanca de fuerzas que actúan sobre un objeto. Además, presenta ejemplos numéricos para demostrar estos conceptos.

1. Universidad Tecnológica de Guaymas
Física
Integrantes:
Arvizu Partida Julia Isabel
Gutiérrez Martínez Damaris Azucena
Vargas Delgado Carlos David
Técnico Superior Universitario Procesos Industriales, Área
Manufacturada
Principios de estática, condiciones de equilibrio y
momentos de torsión

3. Principios de estática
Que es estática: Es una rama dela mecánica cuyo objetivo
es estudiar las condiciones que deben de cumplir las
fuerzas que actúan sobre un cuerpo, para que este se
encuentre en equilibrio.

4. Los principios de la estática son:
• Paralelogramo
• Equilibrio
• la transmisibilidad, acción y reacción

5. Paralelogramo
Explicación del principio del paralelogramo: Establece que dos
fuerzas que actúan sobre una partícula pueden ser sustituidas
por una sola fuerza llamada resultante, que se obtiene al trazar
la diagonal del paralelogramo que tienene los lados iguales a las
fuerzas dadas.

6. Principio del equilibrio
• Un cuerpo se encuentra en equilibrio cuando no tiene
aceleración, por lo tanto solo hay 2 posibilidades: esta en
reposo o se mueve en línea recta con velocidad
constante
Equilibrio
Equilibrio estático Equilibrio cinético
Equilibrio de traslación Equilibrio de rotacion

7. Principio de la transmisibilidad
Este principio indica que una fuerza que actúa sobre un
cuerpo rígido es equivalente a otro del mismo modulo que
actúa sobre otro punto del cuerpo rígido sobre la misma
recta de acción.

8. Principio de acción y reacción
Toda acción aplica la existencia de una reacción tiene la
misma intensidad pero sentido contrario
(A1 sostener la pesa con la mano, la mano ejerce una
fuerza en sentido opuesto a la fuerza gravitacional, es
decir, en sentido vertical hacia arriba; de lo contrario la
pesa seguirá su trayectoria de caída libre.)

10. Las condiciones de equilibrio son las leyes que rigen la
estática. La estática es la ciencia que estudia las fuerzas que
se aplican a un cuerpo para describir un sistema en equilibrio.
Diremos que un sistema está en equilibrio cuando los cuerpos
que lo forman están en reposo, es decir, sin movimiento. Las
fuerzas que se aplican sobre un cuerpo pueden ser de tres
formas:
• Fuerzas angulares
• Fuerzas coplanares
• Fuerzas paralelas
Condiciones de equilibrio

11. Fuerzas angulares: Dos fuerzas
se dice que son angulares,
cuando actúan sobre un mismo
punto formando un
ángulo.
Fuerzas colineales: Dos fuerzas
son colineales cuando la recta de
acción es la misma, aunque las
fuerzas pueden estar en la misma
dirección o en direcciones opuestas.

12. Fuerzas paralelas: Dos fuerzas son paralelas cuando sus
direcciones son paralelas, es decir, las rectas de acción son
paralelas, pudiendo también aplicarse en la misma dirección
o en sentido contrario.
A nuestro alrededor podemos encontrar numerosos cuerpos
que se encuentran en equilibrio. La explicación física para
que esto ocurra se debe a las condiciones de equilibrio

13. Primera condición de equilibrio: Diremos que un cuerpo se encuentra
en equilibrio de traslación cuando la fuerza resultante de todas las
fuerzas que actúan sobre él es nula: ∑ F = 0.
Un cuerpo se encuentra en estado de
equilibrio traslacional sólo si la suma
vectorial de las fuerzas que actúan
sobre él es igual a cero.
Cuando un cuerpo está en equilibrio, la
resultante de todas las fuerzas que
actúan sobre él es cero. En este caso,
Rx como Ry debe ser cero; es la
condición para que un cuerpo esté en
equilibrio:

14. Ejemplo:
Una pelota de 100N suspendida por una cuerda A es tirada
hacia un lado en forma horizontal mediante otra cuerda B y
sostenida de tal manera que la cuerda A forma un ángulo de
30° con el poste vertical ¿ encuentre las tensiones en las
cuerdas A y B?

15. Ahora se aplica la primera condición de
equilibrio. La suma de las fuerzas a lo largo
del eje X:
SFx = B – A cos 60° = 0
B = A cos 60° = 0.5 A (1)
Ahora al sumar las componentes en Y:
S Fy = A sen 60° - 100N = 0
Por lo que:
A sen 60° = 100N
Ahora se despejan las fuerzas desconocidas:
(sen 60° = .8660)
.8660 A = 100N
A = 100N / .8660 = 115N
Conocemos el valor de A, ahora despejamos
B de la ecuación 1:
B = 0.5 A = (0.5)(115N) = 57.5N

16. Segunda condición de equilibrio
Por otro lado, diremos que un cuerpo está en equilibrio de
rotación cuando la suma de todas las fuerzas que se ejercen
en él respecto a cualquier punto es nula. O dicho de otro
modo, cuando la suma de los momentos de torsión es cero.

18. Brazo de palanca
La distancia perpendicular del eje de rotación a la línea de
acción de la fuerza se llama brazo de palanca de la fuerza, el
cual determina la eficacia de una fuerza dada para provocar
el movimiento rotacional.

19. Formula
𝑟 = 𝑙 sin 𝜃
𝑟 = 𝑙 cos 𝜃
• 𝑟 = Brazo de palanca
• 𝑙 = Longitud
• sin 𝜃 = Grados
• cos 𝜃 = Grados

20. Ejercicio No. 1
• Identifique el brazo de palanca de la fuerza F sobre un
eje en el punto A y calcule el brazo de palanca sobre el
eje B ¿Cuál es la magnitud del brazo de palanca?
Formula: 𝑟 = 𝑙 sin𝜃
Respuesta:
Eje A
𝑙 = 2 𝑓𝑡
sin 𝜃 = 25°
𝑟𝐴 = 2 𝑓𝑡 𝑠𝑖𝑛25°
𝑟𝐴 = 0.845 𝑓𝑡
Eje B
𝑙 = 3 𝑓𝑡
sin 𝜃 = 25°
𝑟𝐵 = 3 𝑓𝑡 𝑠𝑖𝑛25°
𝑟𝐵 = 2.71 𝑓𝑡

21. Ejercicio No. 2
Calcule el brazo de palanca sobre el eje A de la figura y el
eje B.
Formula: 𝑟 = 𝑙𝑐𝑜𝑠𝜃
Respuesta:
Eje A
𝑙 = 2 𝑚
𝑐𝑜𝑠𝜃 = 30°
𝑟 = (2 𝑚 )(cos 30°)
𝑟 = 1.73 𝑚
𝐸𝑗𝑒 B
𝑙 = 5 𝑚
𝑐𝑜𝑠𝜃 = 30°
𝑟 = (5 𝑚 )(cos 30°)
𝑟 = 4.33 𝑚

22. Momentos de torsión
Se ha definido la fuerza como un tirón o un empujón que tiende
a causar un movimiento. El momento de torsión t se define
como la tendencia a producir un cambio en el movimiento
rotacional. El movimiento rotacional se ve afectado tanto por la
magnitud de una fuerza F como por su brazo de palanca r. Por
tanto, definiremos el momento de torsión como el producto de
una fuerza por su brazo de palanca.

23. Las unidades del momento de torsión son las unidades de
fuerza por distancia, por ejemplo, newton-metro (N . m) y
libra-pie (lb . ft.).
Esta aplicación se
encuentran en muchas
herramientas comunes
en el hogar o la industria
donde es necesario girar,
apretar o aflojar
dispositivos.

24. Momento de torsión = fuerza X brazo de palanca
𝜏 = 𝑟 𝑥 𝐹
• 𝜏 = Momento de torsión
• 𝐹 = Fuerza
• 𝑟= Brazo de palanca

25. Dirección del momento de torsión
La dirección del momento de torsión depende de si éste tiende a
producir la rotación en el sentido de avance de las manecillas
del reloj. Si la fuerza F tiende a producir una rotación contraria a
la de las manecillas con respecto a un eje, el momento de
torsión se considerará positivo. Los momentos de torsión en el
sentido de avance de las manecillas del reloj se considerarán
negativos.

27. Ejercicio No.1
• Un mecánico ejerce una fuerza de 20 lb en el extremo de una llave
inglesa de 10 in, este tirón forma un ángulo de 60° con el mango de
la llave, ¿cuál es el momento de torsión producido en la tuerca?
Respuesta:
𝑓 = 20 𝑙𝑏
𝑙 = 10 𝑖𝑛
𝑠𝑖𝑛𝜃 = 60°
𝑟=𝑙 sin𝜃
𝜏 = 𝑟 𝑥 𝐹
Formulas:
𝑟 = (10 𝑖𝑛)sin 60°
𝒓 = 𝟖. 𝟔𝟔 𝒊𝒏
𝜏 = 20 𝑙𝑏 8.66 𝑖𝑛
𝝉 = 𝟏𝟕𝟑 𝒍𝒃 ∙ 𝒊𝒏

28. Ejercicio No. 2
• Si la fuerza F es igual a 80 lb, ¿cuál es el momento de
torsión respecto al eje A (considerando insignificante el
peso de la varilla)?
Formula: 𝜏 = 𝑟 𝑥 𝐹
Respuesta:
𝑟 = 0.845 𝑓𝑡
𝑓 = 80 𝑙𝑏
𝜏 = 0.845 𝑓𝑡 80 𝑙𝑏
𝜏 = 67.6 𝑓𝑡 ∙ 𝑙b

29. Ejercicio No. 3
• Una fuerza de 80 N actúa en el extremo de una llave de 12 cm
como se muestra. Encuentre el momento de torsión.
Respuesta:
𝑓 = 80 𝑁
𝑙 =12 cm
sin𝜃 60°
𝑟 = (12 𝑐𝑚 )sin 60°
𝒓 = 𝟏𝟎. 𝟑𝟗 𝒄𝒎
𝜏 = 80 𝑁 10.39 𝑐𝑚
𝝉 = 𝟖𝟑𝟏. 𝟐 𝑵 ∙ 𝒄𝒎

30. Momento de torsión resultante
Este procedimiento se aplica a fuerzas que tienen un punto de
intersección común. Las fuerzas que carecen de una línea de
acción común producen una resultante del momento de torsión,
además de una resultante de la fuerza traslacional. Cuando las
fuerzas aplicadas actúan en el mismo plano, el momento de
torsión resultante es la suma algebraica de los momentos de
torsión positivos y negativos debidos a cada fuerza.

31. Ejercicio No. 1
• Una pieza angular de hierro gira sobre un punto A, como se observa en
la figura. Determine el momento de torsión resultante en A debido a las
fuerzas de 60 N y 80 N que actúan al mismo tiempo.
Respuesta:
𝑓1 = 60 𝑁
𝑓2 = 80 𝑁
𝑙1 = 12 𝑐𝑚
𝑙2 = 10 𝑐𝑚
𝑟1 =?
𝑟2 = ?
𝑠𝑖𝑛𝜃 = 50°
𝑠𝑖𝑛𝜃 = 70°
𝝉𝒓= 𝝉𝟏 + 𝝉𝟐
𝑡𝑟 = − 60 𝑁 9.14 𝑐𝑚 + 80 𝑁 9.40 𝑐𝑚
𝑡𝑟 = −548.4 𝑁 ∙ 𝑐𝑚 + 752 𝑁 ∙ 𝑐𝑚
𝑡𝑟 = 203.6 𝑁 ∙ 𝑐𝑚
𝑟 = 𝑙 sin𝜃
𝑟1 = 12 𝑐𝑚 sin 50°
𝑟1 = 9.19 𝑐𝑚
𝑟2 = (10𝑐𝑚) sin 70°
𝑟2 = 9.40 𝑐𝑚
𝑟 = 𝑙𝑠𝑖𝑛𝜃
𝑡 = 𝐹𝑟
𝜏𝑟 = 𝜏1 + 𝜏2
Fórmulas:

32. Ejercicio No.2
• ¿Cuál es el momento de torsión resultante respecto al
pivote? Considere que el peso de la barra curva es
insignificante.
Respuesta:
𝑓1 = 80 N
𝑓2 = 200𝑁
𝑙1 = 60 𝑐𝑚
𝑙2 = 40 𝑐 𝑚
𝝉𝒓= 𝝉𝟏 + 𝝉𝟐
𝑡𝑟 = − 80 𝑁 60 𝑐𝑚 + 200 𝑁 25.71 𝑐𝑚
𝑡𝑟 = −4800 𝑁 ∙ 𝑐𝑚 + 5142 𝑁 ∙ 𝑐𝑚
𝑡𝑟 = 342 𝑁 ∙ 𝑐𝑚
𝑟 = 𝑙 sin𝜃
𝑟1 = 60 𝑐𝑚 sin 90°
𝑟1 = 60 𝑐𝑚
𝑟2 = (40 𝑐𝑚) sin 40°
𝑟2 = 25.71𝑐𝑚

33. Ejercicio No. 3
• ¿Cuál es el momento de torsión resultante respecto al punto
A de la figura? No tome en cuenta el peso de la barra.
Respuesta:
𝑓1 = 30 N
𝑓2 = 15 𝑁
𝑓3 = 20 𝑁
𝑙1 = 6 𝑚
𝑙2 = 2 𝑚
𝑙3 = 3𝑚
𝝉𝒓 = 𝝉𝟏 + 𝝉𝟐 + 𝝉𝟑
𝑡𝑟 = 30 𝑁 6 𝑀 + −15 𝑁 2 𝑚 + (−20 𝑁)(3 𝑚)
𝑡𝑟 = 180 𝑁 ∙ 𝑚 − 30 𝑁 ∙ 𝑚 − 60 𝑁 ∙ 𝑚
𝑡𝑟 = 150 𝑁 ∙ 𝑚 − 60 𝑁 ∙ 𝑚
𝑡𝑟 = 90 𝑁 ∙ 𝑚
Fórmulas:

34. Equilibrio rotacional
Un cuerpo en equilibrio rotacional no tiene un momento de torsión
resultante que actúe sobre él. En tales casos, la suma de todos los
momentos de torsión respecto a cualquier eje debe ser igual a cero.
Los ejes pueden elegirse en cualquier parte puesto que el sistema no
tiene la tendencia a girar respecto a cualquier punto.
ΣT = 0 La suma de todos los momentos de torsión respecto
a cualquier punto es cero. ( segunda condición de equilibrio).

35. Ejercicio No. 1
• Suponga que la barra de la figura tiene un peso
insignificante. Halle las fuerzas F y A considerando que el
sistema está en equilibrio. Respuesta:
𝑓1 = 80 N
𝐹 =?
𝐴 =?
ΣT = 0
෍ 𝒕𝟏 + 𝒕𝟐
෍ 𝑡 = − 80 𝑁 30 𝑐𝑚 + 𝐴 90 𝑐𝑚 = 0
෍ 𝑡 = −2400 𝑁 ∙ 𝑐𝑚 + 𝐴 (90𝑐𝑚) = 0
෍ 𝑡 = 𝐴 90 𝑐𝑚 = 2400 𝑁 ∙ 𝑐𝑚
෍ 𝑡 = 𝐴 =
2400 𝑁 ∙ 𝑐𝑚
90 𝑐𝑚
𝐴 = 26.7 𝑁
෍ 𝑡 = −80 𝑁 + (−26.7 𝑁)
𝐹 = −106.7 𝑁
𝜏 = 𝑟 𝑥 𝐹
𝑙1 = 30 𝑐𝑚
𝑙2 = 90 𝑐 𝑚