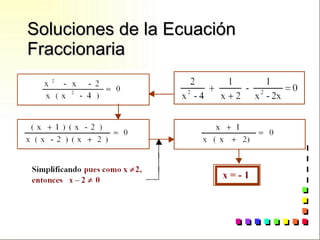
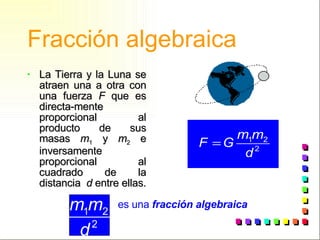
Una expresión algebraica es una expresión que relaciona valores indeterminados con constantes y operaciones matemáticas. Existen diferentes tipos de expresiones algebraicas como racionales, irracionales, enteras y fraccionarias. Los polinomios son expresiones algebraicas formadas por la suma de términos que son el producto de un coeficiente y una potencia de la variable.

1. Expresiones Algebraicas Una expresión algebraica es una expresión en la que se relacionan valores indeterminados con constantes y cifras, todas ellas ligadas por un número finito de operaciones de suma, resta, producto, cociente, potencia y raíz. Ejemplos

2. Tipos de Expresiones Algebraicas Expresiones Algebraicas Racionales Irracionales Enteras Fraccionarias

3. Expresión Algebraica Racional Es racional cuando las variables no están afectadas por la radicación Ejemplo

4. Expresión Algebraica Irracional Es irracional cuando las variables están afectadas por la radicación Ejemplo

5. Expr.Algebraica Racional Entera Una expresión algebraicas es racional entera cuando la indeterminada está afectada sólo por operaciones de suma, resta, multiplicación y potencia natural. Ejemplo

6. Expresión Algebraica Racional Fraccionaria Una expresión algebraicas racional es fraccionaria cuando la indeterminada aparece en algún denominador. Ejemplo

7. Polinomios Son las expresiones algebraicas más usadas. Sean a 0 , a 1 , a 2 , …, a n números reales y n un número natural, llamaremos polinomio en indeterminada x a toda expresión algebraica entera de la forma: a 0 + a 1 x + a 2 x 2 + … + a n x n

8. Ejemplos de polinomios A los polinomios en indeterminada x los simbolizaremos con letras mayúsculas indicando la indeterminada entre paréntesis: P(x) ; Q(x) ; T(x).

9. Términos Monomio : polinomio con un solo término. Binomio : polinomio con dos términos. Trinomio : polinomio con tres términos. Cada monomio a i x i se llama término . El polinomio será de grado n si el término de mayor grado es a n x n con a n  0. A a 0 se lo llama término independiente . A a n se lo llama término principal .

10. Ejemplos El polinomio 0 + 0x + 0x 2 + … +0x n se llama polinomio nulo . Lo simbolizaremos por O p (x) . No se le asigna grado.

11. Ejercicio Indicar cuáles de las siguientes expresiones algebraicas son polinomios. En este último caso indicar su grado.

12. Polinomios iguales Dos polinomios son iguales si y sólo si los coeficientes de los términos de igual grado lo son. Ejercicio: Determinar a, b y c para que P(x)=Q(x)

13. Suma de Polinomios Para sumar dos polinomios se agrupan los términos del mismo grado y se suman sus coeficientes. Ejemplo: Sumar los siguientes polinomios P(x) = -2x 4 + 5x 3 – 3x + 1 Q(x) = 3x 3 – 6x 2 – 5x - 2

14. Propiedades de la Suma Asociativa Conmutativa Existencia de elemento neutro Existencia de elemento opuesto

15. Resta de Polinomios Para restar el polinomio Q(x) del polinomio P(x) se debe sumar a P(x) el opuesto de Q(x). P(x) – Q(x) = P(x) + [ - Q(x) ] Ejemplo: Restar los siguientes polinomios P(x) = -2x 4 + 5x 3 – 3x + 1 Q(x) = 3x 3 – 6x 2 – 5x - 2

16. Multiplicación de Polinomios Para multiplicar dos polinomios se multiplica cada monomio de uno de ellos por cada uno de los términos del otro y luego se suman los términos de igual grado. Ejemplo: Multiplicar los siguientes polinomios P(x) = -2x 4 + 5x 3 – 3x + 1 Q(x) = 3x 3 – 6x 2 – 5x – 2 P(x).Q(x) = P(x) 3x 3 + P(x) (-6x 2 ) + P(x) (-5x ) + P(x)(-2)

17. Propiedades del Producto Asociativa Conmutativa Existencia de elemento neutro.

18. Algunos productos importantes (x+a) 2 =(x+a)(x+a)= x 2 + 2ax + a 2 (x-a) 2 =(x-a)(x-a)= x 2 - 2ax + a 2 (x+a) 3 = x 3 + 3ax 2 + 3a 2 x + a 3 (x-a) 3 = x 3 - 3ax 2 + 3a 2 x - a 3 (x+a)(x-a)= x 2 –ax +ax-a 2 = x 2 -a 2

19. Ejercicio Escribir los desarrollos de

20. Ejercicio : Expresar los siguientes trinomios cuadrados perfectos como el cuadrado de un binomio y a los cuatrinomios cubos perfectos como el cubo de un binomio.

21. Ejercicio : La expresión x 2 - a 2 es una diferencia de cuadrados. Escribir las siguientes diferencias como producto de binomios.

22. División de polinomios Existe una estrecha analogía entre el cociente de polinomios y la división de números enteros. Recordemos algunas definiciones de la división entre números enteros.

23. División entre números enteros En el conjunto de números enteros, si D es el dividendo y d  0 es el divisor, existen y son únicos dos enteros c (cociente) y (r (resto) tales que D = d . C + r 0 ≤ r < |d| Si r=0 se dice que D es divisible por d.

24. División entre números enteros Ejemplo: Realizar las siguientes divisiones enteras: 29 dividido 6 será: c= 4 y r=5 pues 29 = 6 . 4 + 5 y 0 ≤ 5 < 6 29 dividido -6 será: c= -4 y r=5 pues 29 = (-6) . (-4) + 5 y 0 ≤ 5 < |-6| ¿Podría haber sido c = -5 y r = -1?

25. División de polinomios Dados los polinomios D(x) = 6x 3 – 17x 2 +15x-8 d(x) = 3x – 4 determinar, si es posible, dos polinomios c(x) y r(x) tales que D(x) = d(x). C(x) + r(x) de modo que el grado de r(x) sea menor que el grado de d(x) o bien r(x)=O p (x)

26. Ejemplo 6x 3 – 17x 2 + 15x – 8 3x – 4 -6x 3 + 8x 2 2x 2 - 3x + 1 6x 3 -17x 2 +15x-8 = (3x-4)(2x 2 -3x+1)-4 0x 3 - 9x 2 + 15x 9x 2 - 12x 0x 2 + 3x - 8 -3x + 4 0x - 4

27. Ejercicios D(x) = 4x 5 + 2x 3 – 24x 2 + 18x d(x) = x 2 – 3x D(x) = 16x 8 + 24x 6 + 9x 4 d(x) = 4x 5 + 4x 4 + 3x 3 + 3x 2 D(x) = 2x 4 – 6x 3 + 7x 2 – 3x +2 d(x) = x-2

28. División de Polinomios Dados los polinomios D(x) y d(x); d(x)  O p (x), diremos que d(x) divide a D(x) si y sólo si existe un polinomio c(x) tal que D(x) = d(x) . c(x)

29. Ejercicios Dados los polinomios P(x) y Q(x) indica si alguno de ellos es divisible por el otro P(x) = x 4 -2x 3 +x 2 -5x + 1 Q(x) = x 3 + x 2 + x + 1 P(x) = x 4 +2x 3 +4x 2 + 8x +16 Q(x) = x 5 - 32

30. División de un polinomio por otro de la forma (x-a) 3x 3 – 2x 2 – 5x – 9 x – 2 - 3x 3 + 6x 2 3x 2 + 4x + 3 4x 2 – 5x - 4x 2 + 8x 3x – 9 -3x + 6 -3 3 6 4 8 3 6 3x 3 – 2x 2 – 5x – 9 = ( x – 2)(3x 2 + 4x + 3) + (-3) Regla de Ruffini 3 -2 -5 -9 2 -3

31. División de un polinomio por otro de la forma (x-a) División de P(x) = 3x 3 – 2x 2 – 5x – 9 por (x-2) realizada por la Regla de Ruffini 3 -2 -5 -9 2 6 8 6 3 4 3 -3 1º operación : 3.2 -2 = 4 2º operación : (3.2 -2).2 - 5 = 3 3º operación : [3(2) 2 – 2 . 2 - 5].2 -9 =-3 Por lo tanto 3.(2) 2 -2.(2) 2 -5.2 -9 = -3

32. Raíces de un polinomio Un número real a es raíz de un polinomio P(x) si y solo si P(a) = 0 Ejercicio: Verifique que x=1 es raíz del polinomio P(x) = 3x 2 + 2x – 5

33. Raíces de un Polinomio Si un polinomio tiene coeficientes enteros y a es una raíz entera del polinomio entonces a divide al término independiente. Ejercicio: Calcular las raíces de P(x) = 2x 3 - 2x 2 - 16x + 24

34. Ejercicio: Calcular las raíces de P(x) = 2x 3 - 2x 2 - 16x + 24 Si P(x) tiene alguna raíz entera, ésta debe ser divisor de 24. Probar que 1 y -1 no son raíces de P(x) 2x 3 – 2x 2 – 16x + 24 = ( x – 2)(2x 2 + 2x -12) Ver x=2 también es raíz de 2x 2 + 2x -12 2x 2 + 2x -12 = (x-2)(2x+6)

35. Ejercicio Calcular las raíces de P(x) = x 4 - x 3 - 6x 2 + 4x + 8 P(x) = (x-2) 2 (x+1) (x+2)

36. Resolver la siguiente ecuación

37. Soluciones de la Ecuación Fraccionaria

38. Fracción algebraica La Tierra y la Luna se atraen una a otra con una fuerza F que es directa-mente proporcional al producto de sus masas m 1 y m 2 e inversamente proporcional al cuadrado de la distancia d entre ellas. es una fracción algebraica

39. Una fracción algebraica es una expresión de la forma p y q son polinomios, y p se llama el numerador y q se llama el deno-minador de la fracción. Ejemplo son fracciones algebraicas La mecanización de fracciones algebraicas es similar a la mecanización de fracciones comunes aritméticas, por lo que se recordará enseguida la mecanización aritmética de fracciones comunes. Nota en donde

40. Revisión de las operaciones con fracciones comunes Para simplificar una fracción común, se divide el numerador y el denomi-nador entre el máximo común divisor (mcd) de ambos. Ejemplo Simplificar la fracción Solución El mcd de 38 y 57 es 19. Entonces se simplifica así:

41. Locadia viaja en un tren a 24 km por hora, y observa que otro tren estacionado en una vía paralela a la vía por la que viaja, pasa ante ella en 10 segundos. ¿Qué longitud tiene el tren estacionado? Ejemplo Solución La velocidad en metros por segundo del tren en el cual viaja Locadia, se obtiene así: Por tanto la longitud del tren estacionado, se determina como sigue:

42. Ejemplo Solución Dado que la pipa 1 tarda 20 minutos en llenar el depósito, entonces llena parte del depósito en 1 minuto. Dado que la pipa 2 tarda 30 minutos en llenar el depósito, entonces llena parte del depósito en 1 minuto. En una gasolinera hay dos pipas llenando el depósito de gasolina. La pipa 1 lo llena en 20 minutos y la pipa 2 en 30 minu tos. Si durante el tiempo de llenado se consume del depósito por hora, ¿en cuánto tiempo se llena el depósito con las dos pipas llenando juntas?

43. Finalmente, el tiempo en minutos que tardan en llenar el depósito las dos pipas juntas, se calcula así: Dado que se consume del depósito por hora, entonces en un minuto se consume del depósito. Por tanto, lo que las dos pipas juntas llenan del depósito por minuto se calcula como sigue:

44. SIMPLIFICACIÓN DE FRACCIONES ALGEBRAICAS Para simplificar una fracción, se dividen el numerador y el denominador por uno o más factores comunes a ambos. Se obtiene así otra fracción equivalente. Por ejemplo: Simplificar Donde hemos dividido numerador y denominador entre 3, , Para poder simplificar una fracción el numerador y el denominador tiene que estar factorizado. Si no lo están la primera operación ha de ser la de factorizarlos.

45. Simplificar Como vemos el denominador es un polinomio, o sea una suma, por tanto antes de simplificar hay que factorizarlo. En este caso el método adecuado es sacar factor común así

46. Simplificar las siguientes fracciones algebraicas Como ya son productos, tanto el numerador como el denominador, basta dividir numerador y denominador por los factores comunes En esta fracción aparece una suma en el numerador y otra en el denominador, por tanto hay que factorizar ambas cosas. Podemos sacar factor común en el numerador e en el denominador

47. aquí el numerador es una suma pero no se puede factorizar, pero el denominador se puede factorizar ya que es el cuadrado de una suma . aquí sólo podemos factorizar el denominador, que se trata de una diferencia de cuadrados y que es igual a suma por diferencia

48. Multiplicación y división de Fracciones Algebraicas MULTIPLICACIÓN DE FRACCIONES Procedimiento para multiplicar fracciones cuyo producto es irreducible Multiplicar los numeradores, obteniéndose el numerador del producto. Multiplicar los denominadores, obteniéndose el denominador del producto

49. Ejemplo a) b) c) d) e) f)

50. Procedimiento para multiplicar fracciones cuyo producto se puede simplificar Descomponer en factores los polinomios que figuran en los numeradores y denominadores. Dividir por los factores comunes del numerador y denominador. Multiplicar los factores restantes.

51. Multiplica SOLUCIÓN:

52. DIVISIÓN DE FRACCIONES Para dividir una fracción se multiplica por la fracción recíproca Ejemplo Dividir Como se ha indicado, invertimos el divisor y luego procedemos como en la multiplicación. Ejemplo Dividir

53. Fracciones compuestas Las fracciones compuestas son aquellas cuyo numerador y/o denominador son fracciones Ejemplo: ; ;

54. También se pueden presentar fracciones compuestas que contenga en su numerador y/o denominador operaciones, las cuales deben desarrollarse en primer lugar para luego resolver como los casos anteriormente dados. Ejemplo:

55. Adición y Sustracción de Fracciones Algebraicas Adición o sustracción de expresiones racionales con denominadores comunes. Procedimiento Poner el denominador común y sumar algebraicamente los numeradores. Reducir la fracción que resulte. Al sumar algebraicamente los numeradores encerrar cada polinomio numerador en un paréntesis precedido del signo que corresponde a su fracción.

56. Ejemplo b) c)

57. Adición o sustracción de expresiones racionales con denominadores distintos. Para sumar o restar fracciones con denominadores diferentes, primero las convertimos a fracciones que tengan el mismo denominador. Cuando los denominadores son opuesto multiplicamos una de ellas por 1, escrito en la forma , para obtener un común denominador.

58. Ejemplo: Sumar Cuando los denominadores de dos o más fracciones son distintos, en ocasiones es necesario multiplicar una o más fracciones por 1, escrito en la forma adecuada, para obtener un común denominador. SOLUCIÓN:

59. Ejemplo Efectúa la siguiente operación:

60. Hacer las operaciones indicadas SOLUCIÓN: Factorizamos cada denominador para encontrar el MCD= En este caso se puede simplificar el resultado final