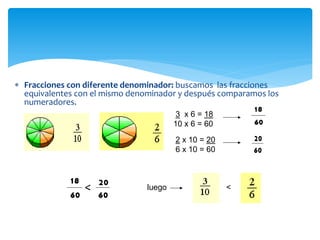
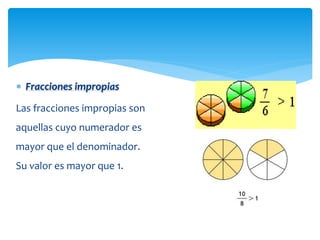
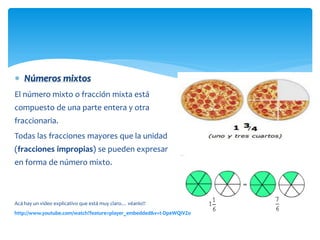
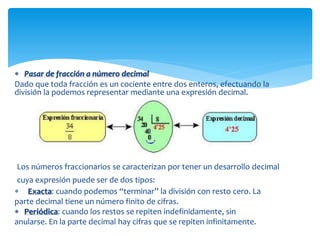
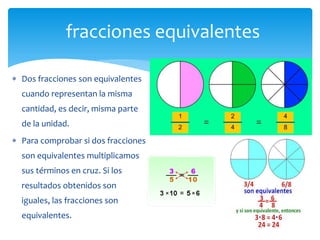
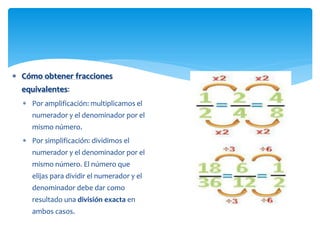
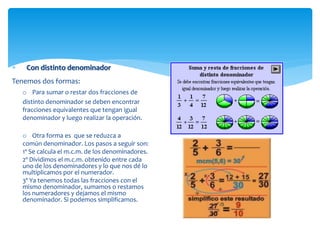
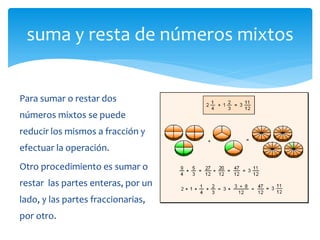
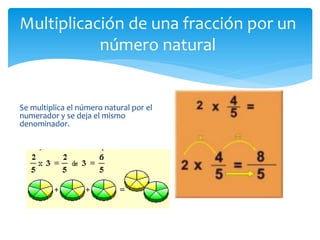
El documento trata sobre fracciones. Explica la historia, definición, lectura, comparación, ubicación en la recta numérica, tipos de fracciones, fracciones equivalentes, simplificación, suma y resta de fracciones y números mixtos, y multiplicación de fracciones por números naturales.