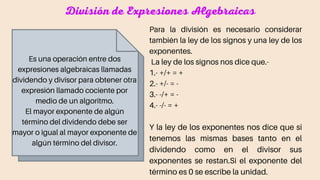
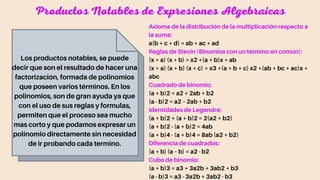
Este documento trata sobre expresiones algebraicas. Explica que una expresión algebraica es una combinación de letras y números ligados por operaciones como la suma, resta, multiplicación y división. Luego describe diferentes tipos de expresiones como monomios, polinomios, binomios y trinomios. También explica cómo realizar operaciones básicas como suma, resta, multiplicación y división con expresiones algebraicas, así como el concepto de valor numérico y la factorización mediante productos notables.

1. Expresiones Algebraicas
República Bolivariana de Venezuela
Ministerio del Poder Popular para la Educación Universitaria
Universidad Politécnica Territorial del estado Lara Andrés Eloy Blanco
Barquisimeto-Iribarren-Lara
Estudiante: Luciana Martelli
PNF: Turismo
Sección: 0100
Profesor: Nelson Torcate

2. Temas a Tratar
2.Suma, Resta y Valor Numérico de Expresiones Algebraicas
3.Multiplicación y División de Expresiones Algebraicas
5.Factorización por Productos Notables
4.Productos Notables de Expresiones Algebraicas
1.Expresiones Algebraicas

3. Una expresión algebraica es
una combinación de letras y
números ligadas por los signos
de las operaciones: adición,
sustracción, multiplicación,
división y potenciación. Las
expresiones algebraicas nos
permiten, por ejemplo, hallar
áreas y volúmenes.
Expresiones Algebraicas
¿Qué Son?:

4. Las expresiones algebraicas
llamadas monomios con aquellas
que están compuestas por un sólo
término. Las únicas operaciones
matemáticas que aparecen son la
multiplicación y la potencia de
exponente natural, es decir, de
exponentes con números positivos.
Un ejemplo sería:
2x²
2x2y3z.
Tipos de Expresiones Algebraicas
Monomios: Polinomios:
Según la cantidad de términos por la
que está formada cambia su nombre:
binomio, trinomio, cuatrinomio,
etcétera. Estas expresiones
algebraicas en general se componen
por dos o más términos, es decir, por
más de un monomio. Los más común
es diferenciar entre binomios y
trinomios, y al resto nombrarlos todos
polinomios. Algunos ejemplos:
x+y+z
ab³ + 5a² b⁷ m – 35 abx⁵

5. Suma de Expresiones Algebraicas
Es la reunión de varias
cantidades algebraicas, tomando
su valor númerico en el sentido
que indica el signo que a cada
expresión lleva. Por lo tanto, la
suma algebraica no supone
aumento, y su valor puede ser
menor que el de cualquier
sumando.
Para sumar expresiones algebraicas se
ponen unas a continuación de otras con
sus mismo signos y se hace después la
reducción de términos semejantes.
Si se suman polinomios, se ponen los
sumandos unos debajo de otros, de
manera que coincidan en forma de
columnas los términos semejantes y
luego se reducen.

6. Ejemplos de Suma Algebraica
Monomio
Polinomio

7. Resta de Expresiones Algebraicas
Es una operación matemática
inversa a la suma algebraica y
tiene por objeto realizar una
diferencia entre expresiones
algebraicas donde el primer
elemento que restaremos se
llama minuendo y el segundo
elemento se le llama
sustraendo.
De la misma manera con la suma algebraica,
con la resta o diferencia algebraica,
debemos tener en cuenta que restar dos
términos semejantes resulta un único
termino semejante, para dos términos no
semejantes, el resultado se deja tal cual es.
Si bien, la suma algebraica no afecta a los
signos operacionales de los términos entre
paréntesis, la resta si afecta a cada termino,
esto es, cambia los signos operacionales de
cada termino luego de eliminar los
paréntesis.

8. Ejemplos de Resta Algebraica
Monomios
(4a)-(-2a)-(-3b)-(-5b)-(2c)-(c)
Eliminando los paréntesis resulta:
4a+2a+3b+5b-2c-c
Reduciendo términos semejantes:
6a+8b-3c
Polinomios
(8m+6n)-(2m-5n)-(-p)
Eliminando los paréntesis resulta:
8m+6n-2m+5n+p
6m+11n+p

9. Valor Numérico de Expresiones Algebraicas
Es el resultado final que se obtiene
al sustituir los valores de todas las
incógnitas que aparecen en la
expresión que nos interesa evaluar
y de realizar todas las operaciones
indicadas respetando el orden
indicado por los signos de
agrupación.
Por ejemplo, si el valor de X es 5,
entonces, el valor de 2X es 10, esto
es: 2x= 2.5= 10
Ejemplo:
Calcular el valor numérico de: x+15
cuando x=2
Sustituimos en la expresión: x+15= 2+15= 17
El valor numérico de la expresión es 17
Calcular el valor numérico de x²-x-10
cuando x=5
Sustituimos en la expresión:
x²-x-10= 5"-5-10= 25-5-10=10
El valor numérico de la expresión es 10

10. Multiplicación de Expresiones Algebraicas
Es una operación matemática
que consiste en obtener un
resultado llamado producto a
partir de dos factores
algebraicos llamada
multiplicando y multiplicador.

11. Ejemplos de Multiplicación Algebraica
Multiplicación de dos monomios:Para esta operación se debe de aplicar la regla de los
signos, los coeficientes se multiplican y las literales cuando son iguales se escribe la literal y se
suman los exponentes, si las literales son diferentes se pone cada literal con su
correspondiente exponente.3x3y2 por 7x4
(3x3y2)(7x4)
Se realiza de la siguiente forma: los coeficientes se multiplican, el exponente de x es la suma de
los exponentes que tiene en cada factor y como y solo esta en uno de los factores se escribe y
con su propio exponente.
(3)(7)x3+4y2
21x7y2
Multiplicación de un monomio por un polinomio:Para esta operación se debe multiplicar el
monomio por cada uno de los monomios que forman al polinomio, ejemplo:
3 * (2x3-3x2+4x-2)
(3 * 2x3) + (3 * -3x2) + (3 * 4x) + (3 * -2)
6x3-9x2+12x-6

12. Multiplicación de un polinomio por otro polinomio:
En esta operación debe de multiplicar cada uno de los monomios de un
polinomio por todos los monomios del otro polinomio, por ejemplo:
(2x2-3) * (2x3-3x2+4x)
(2x2*2x3) + (2x2*-3x2) + (2x2*4x) + (-3*2x3) + (-3*-3x2) + (-3*4x)
4x5-6x4+8x3-6x3+9x2-12x

13. División de Expresiones Algebraicas
Es una operación entre dos
expresiones algebraicas llamadas
dividendo y divisor para obtener otra
expresión llamado cociente por
medio de un algoritmo.
El mayor exponente de algún
término del dividendo debe ser
mayor o igual al mayor exponente de
algún término del divisor.
Para la división es necesario considerar
también la ley de los signos y una ley de los
exponentes.
La ley de los signos nos dice que.-
1.- +/+ = +
2.- +/- = -
3.- -/+ = -
4.- -/- = +
Y la ley de los exponentes nos dice que si
tenemos las mismas bases tanto en el
dividendo como en el divisor sus
exponentes se restan.Si el exponente del
término es 0 se escribe la unidad.

14. Ejemplos de División Algebraica
División de monomios: Se dividen los coeficientes y las literales se restan junto con sus
exponentes.
Ejemplo.- 5xm+2y4z / -4xm-4y3z = 5/4 x6y
División de polinomio entre monomio: Se realiza dividiendo cada uno de los factores del
polinomio entre el factor del monomio.
Ejemplo.- 3ª3-6ª2b+9ab2 / 3ª=a2-2ab+3b2
División de polinomios: Para dividir un polinomio entre otro polinomio es necesario seguir los
siguientes pasos.
1.- Se ordenan los 2 polinomios en orden descendente y alfabético.
2.- Se divide el primer término del dividendo entre el primer término del divisor.
3.- Se multiplica el primer término del cociente por el divisor y el producto obtenido se resta del
dividendo, obteniendo un nuevo dividendo.
4.- Se repiten los pasos 2 y 3 hasta que el resultado sea 0 o de menor exponente que el
dividendo.
Ejemplo.- -15x2+22xy-8y2 / -3x+2y = 5x-4y

15. Productos Notables de Expresiones Algebraicas
Los productos notables, se puede
decir que son el resultado de hacer una
factorización, formada de polinomios
que poseen varios términos. En los
polinomios, son de gran ayuda ya que
con el uso de sus reglas y formulas,
permiten que el proceso sea mucho
mas corto y que podamos expresar un
polinomio directamente sin necesidad
de ir probando cada termino.
Axioma de la distribución de la multiplicación respecto a
la suma:
a(b + c + d) = ab + ac + ad
Reglas de Stevin (Binomios con un término en común):
(x + a) (x + b) = x2 +(a + b)x + ab
(x + a) (x + b) (x + c) = x3 +(a + b + c) x2 +(ab + bc + ac)x +
abc
Cuadrado de binomio:
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 – 2ab + b2
Identidades de Legendre:
(a + b)2 + (a + b)2 = 2(a2 + b2)
(a + b)2 - (a + b)2 = 4ab
(a + b)4 - (a + b)4 = 8ab (a2 + b2)
Diferencia de cuadrados:
(a + b) (a – b) = a2 - b2
Cubo de binomio:
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a - b)3 = a3 - 3a2b + 3ab2 - b3

16. Factorización porProductos Notables
Es el proceso de encontrar dos o
más expresiones cuyo producto
sea igual a una expresión dada; es
decir, consiste en transformar a
dicho polinomio como el
producto de dos o más factores.
Encontrar los polinomios raíz de
otros más complejos.
Factor Común: Consiste en simplificar todos
los términos del polinomio por un mismo
coeficiente, ya sea una letra o un numero, o la
combinación de ellos.
6xyˆ3 - 9nxˆ2yˆ3 + 12nxˆ3yˆ3 - 3nˆ2xˆ4yˆ3
- Todos los términos son divisibles entre 3
- En todos los términos hay X y Y, N no está en
todos los términos. El menor exponente de X
es 1, y el menor exponente de Y es 3.
- El factor común es 3xyˆ3
6xyˆ3 - 9nxˆ2yˆ3 + 12nxˆ3yˆ3 + 3nˆ2xˆ4yˆ3
/3xyˆ3= 2 - 3nx + 4nxˆ2 - nˆ2xˆ3
El resultado se expresa: 3xyˆ3(2 - 3nx + 4nxˆ2 -
nˆ2xˆ3)

17. Bibliografía
Expresiones Algebraicas: https://conceptodefinicion.de/expresiones-
algebraicas/#!/bounceback
https://es.plusmaths.com/clasificacion-de-las-expresiones-algebraicas.html
Suma, Resta y Valor Numérico de Expresiones Algebraicas:
https://algemetria.com/adicion-y-sustraccion/
https://ciencias-basicas.com/matematica/elemental/operaciones-algebraicas/resta-
algebraica/
https://www.celeberrima.com/ejemplos-valor-numerico-de-una-expresion-
algebraica/
Multiplicación de Expresiones Algebraicas: https://ciencias-
basicas.com/matematica/elemental/operaciones-algebraicas/multiplicacion-
algebraica/#ejercicios-resueltos
http://cidecame.uaeh.edu.mx/lcc/mapa/PROYECTO/libro1/153_multiplicacin_de_ex
presiones_algebraicas.html

18. División de Expresiones Algebraicas: https://ciencias-
basicas.com/matematica/elemental/operaciones-algebraicas/5-division-algebraica/
https://sites.google.com/site/soportymantenec1c/parcial-2/division-de-expresiones-
algebraicas
Productos Notables de Expresiones Algebraicas:
https://wikimat.es/polinomios/productos-notables/
https://es.wikibooks.org/wiki/Matem%C3%A1ticas/%C3%81lgebra/Productos_Notab
les#Factorizaci%C3%B3n
Factorización por Productos Notables:
https://es.wikibooks.org/wiki/Matem%C3%A1ticas/%C3%81lgebra/Productos_Notab
les#Factorizaci%C3%B3n