Este documento presenta fórmulas y tablas estadísticas de varios capítulos relacionados con estadística descriptiva, probabilidad, distribuciones de probabilidad, intervalos de confianza, pruebas de hipótesis y análisis de varianza. Incluye fórmulas para calcular la media, desviación estándar, probabilidad binomial y normal, intervalos de confianza, pruebas t, z y qui-cuadrado, correlación, regresión y análisis de varianza de uno y dos factores.

1. Fórmulas y tablas
para Estadística, décima edición, de Mario Triola
D.R. © 2006 Pearson Educación de México S.A. de C.V.
Capítulo 3: Estadística descriptiva
ϭ Media
ϭ Media (tabla de frecuencias)
s ϭ Desviación estándar
s ϭ
s ϭ
Varianza ϭ s2
Capítulo 4: Probabilidad
si A y B son mutuamente
excluyentes
si A y B no son mutuamente excluyentes
si A y B son independientes
si A, B son dependientes
Regla de los sucesos complementarios
Permutaciones (sin elementos iguales)
Permutaciones (n1 iguales,…)
Combinaciones
Capítulo 5: Distribuciones de probabilidad
Media (distribución de probabilidad)
Desviación estándar (dist. de prob.)
Probabilidad binomial
Media (binomial)
Varianza (binomial)
Desviación estándar (binomial)
Capítulo 6: Distribución normal
Puntuación estándar
Teorema del límite central
Teorema del límite central
(error estándar)
␴xϪ ϭ
␴
͙n
␮xϪ ϭ ␮
z ϭ
x Ϫ x
s
or
x Ϫ ␮
␴
Distribución de Poisson
donde e Ϸ 2.71828P(x) ϭ
␮x
. eϪ␮
x!
␴ ϭ ͙n . p . q
␴2
ϭ n . p . q
␮ ϭ n . p
P(x) ϭ
n!
(n Ϫ x)! x!
. px . qnϪx
␴ ϭ ͙[⌺x2 . P(x)] Ϫ ␮2
␮ ϭ ⌺x . P(x)
nCr 5
n!
(n 2 r)! r!
n!
n1! n2! . . . nk!
nPr 5
n!
(n 2 r)!
P(A) 5 1 2 P(A)
P(A y B) 5 P(A) . P(B 0A)
P(A y B) 5 P(A) . P(B)
P(A o B) 5 P(A) 1 P(B) 2 P(A y B)
P(A o B) 5 P(A) 1 P(B)
Desviación estándar
(tabla de frecuencias)Å
n3S(f . x2
)4 2 3S(f . x)42
n(n 2 1)
Desviación estándar
(método rápido)Å
n(Sx2
) 2 (Sx)2
n(n 2 1)
Å
S(x 2 x)2
n 2 1
Sf . x
Sf
x
Sx
n
x
Capítulo 7: Intervalos de confianza (una población)
ˆp Ϫ E Ͻ p Ͻ ˆp ϩ E Proporción
donde
Media
donde (s conocida)
o (s desconocida)
Varianza
Capítulo 7: Determinación de tamaño de muestra
Proporción
Proporción (ˆp y ˆq conocidas)
Media
Capítulo 9: Intervalos de confianza (dos poblaciones)
donde
(Indep.)
donde
(s1 y s2 desconocidas y se supone que no son iguales)
(s1 y s2 desconocidas, pero se supone que son iguales)
(s1, s2 conocidas)
(Datos apareados)
donde (gl ϭ n Ϫ 1)E 5 ta>2
sd
!n
d 2 E , md , d 1 E
E 5 za>2
Å
s2
1
n1
1
s2
2
n2
s2
p 5
(n1 2 1)s2
1 1 (n2 2 1)s2
2
(n1 2 1) 1 (n2 2 1)
E 5 ta>2
Å
s2
p
n1
1
s2
p
n2
(gl 5 n1 1 n2 2 2)
(gl ϭ el menor de
n1 Ϫ 1, n2 Ϫ 1)E 5 ta>2
Å
s2
1
n1
1
s2
2
n2
(x1 2 x2) 2 E , (m1 2 m2) , (x1 2 x2) 1 E
E 5 za>2
Å
pˆ1qˆ1
n1
1
pˆ2qˆ2
n2
(pˆ1 2 pˆ2) 2 E , (p1 2 p2) , (pˆ1 2 pˆ2) 1 E
n 5 B
za>2s
E
R
2
n 5
3za>242
pˆ qˆ
E2
n 5
3za>242 . 0.25
E2
(n 2 1)s2
x2
R
, s2
,
(n 2 1)s2
x2
L
E 5 ta>2
s
!n
E 5 za>2
s
!n
x 2 E , m , x 1 E
E 5 za>2
Å
pˆ qˆ
n
‹
‹
‹

2. Fórmulas y tablas
para Estadística, décima edición, de Mario Triola
D.R. © 2006 Pearson Educación de México S.A. de C.V
Capítulo 8: Estadísticos de prueba (una población)
Proporción: una población
Capítulo 9: Estadísticos de prueba (dos poblaciones)
Dos proporciones
Dos medias: independiente; s1 y s2 desconocidas y no se
supone que sean iguales.
Dos medias: independiente; s1 y s2 desconocidas, pero
se supone que son iguales.
Capítulo 11: Multinomiales y tablas de contingencia
donde
Prueba de McNemar
para pares apareados
(gl ϭ 1)
x2
5
(0 b 2 c 0 2 1)2
b 1 c
E 5
(total por renglón)(total por columna)
(gran total)
Tabla de contingencia
[gl ϭ (r Ϫ 1)(c Ϫ 1)]x2
5 g
(O 2 E)2
E
Multinomial
(gl ϭ k Ϫ 1)x2
5 g
(O 2 E)2
E
Desviación estándar o varianza: dos
poblaciones (donde s2
1 Ն s2
2)
F 5
s2
1
s2
2
Dos medias: datos apareados
(gl ϭ n Ϫ 1)t 5
d 2 md
sd>!n
Dos medias: independiente;
s1, s2 conocidas.
z 5
(x1 2 x2) 2 (m1 2 m2)
Å
s2
1
n1
1
s2
2
n2
s2
p 5
(n1 2 1)s2
1 1 (n2 2 1)s2
2
n1 1 n2 2 2
t 5
(x1 2 x2) 2 (m1 2 m2)
Å
s2
p
n1
1
s2
p
n2
gl ϭ el menor de
n1 Ϫ 1, n2 Ϫ 1t 5
(x1 2 x2) 2 (m1 2 m2)
Å
s2
1
n1
1
s2
2
n2
z 5
(pˆ1 2 pˆ2) 2 (p1 2 p2)
Å
pq
n1
1
pq
n2
Desviación estándar o varianza:
una poblaciónx2
5
(n 2 1)s2
s2
Media: una población
(s desconocida)t 5
x 2 m
s> !n
Media: una población
(s conocida)z 5
x 2 m
s>!n
z 5
pˆ 2 p
Å
pq
n
Capítulo 10: Correlación lineal/Regresión
Correlación
Ecuación estimada de la recta de regresión
Intervalo de predicción
donde
Capítulo 12: Análisis de varianza de un factor
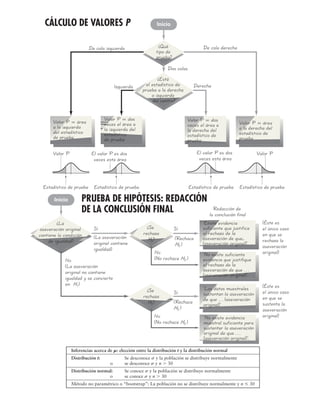
1. Usar un programa de cómputo o una calculadora para
obtener los resultados.
2. Identificar el valor P.
3. Obtener la conclusión:
Si el valor Յ a, se rechaza la hipótesis nula de medias
iguales.
Si P Ͼ a, no se rechaza la hipótesis nula de medias
iguales.
Capítulo 12: Análisis de varianza de dos factores
Procedimiento:
1. Usar un programa de cómputo o una calculadora para
obtener los resultados.
2. Probar H0: No hay una interacción entre el factor de
renglón y el factor de columna.
3. Detenerse si se rechaza H0 del paso 2.
Si no se rechaza H0 del paso 1 (de manera que al parecer
no existe un efecto de interacción), continúe con las
siguientes dos pruebas:
Prueba de los efectos del factor de renglón.
Prueba de los efectos del factor de columna.
Procedimiento para poner a prueba H0: m1 5 m2 5 m3 5 c
E ϭ t␣͞2se ͱ1 ϩ
1
n
ϩ
n(x0 Ϫ x)2
n(⌺x2
) Ϫ (⌺x)2
yˆ Ϫ E Ͻ y Ͻ yˆ ϩ E
se 5
Å
S(y 2 yˆ )2
n 2 2
o
Å
Sy2
2 b0Sy 2 b1Sxy
n 2 2
r2
5
variación explicada
variación total
yˆ 5 b0 1 b1x
b0 5 y 2 b1x or b0 5
(Sy)(Sx2
) 2 (Sx)(Sxy)
n(Sx2
) 2 (Sx)2
b1 5
nSxy 2 (Sx)(Sy)
n(Sx2
) 2 (Sx)2
r 5
nSxy 2 (Sx)(Sy)
"n(Sx2
) 2 (Sx)2
"n(Sy2
) 2 (Sy)2
‹‹
‹

3. TABLA A-6
Valores críticos del coeficiente
de correlación r de Pearson
n a ϭ .05 a ϭ .01
4 .950 .999
5 .878 .959
6 .811 .917
7 .754 .875
8 .707 .834
9 .666 .798
10 .632 .765
11 .602 .735
12 .576 .708
13 .553 .684
14 .532 .661
15 .514 .641
16 .497 .623
17 .482 .606
18 .468 .590
19 .456 .575
20 .444 .561
25 .396 .505
30 .361 .463
35 .335 .430
40 .312 .402
45 .294 .378
50 .279 .361
60 .254 .330
70 .236 .305
80 .220 .286
90 .207 .269
100 .196 .256
NOTA: Para probar H0: r ϭ 0 contra H1: r ϶ 0,
se rechaza H0 si el valor absoluto de r es mayor
que el valor crítico que se indica en la tabla.
Capítulo 13: Pruebas no paramétricas
Prueba del signo para n Ͼ 25
Prueba de Kruskal-Wallis (chi cuadrada, gl ϭ k Ϫ 1)
Correlación de rangos
Capítulo 14: Gráficas de control
Gráfica R: Graficar rangos muestrales
LCS:
Línea central:
LCI:
Gráfica : Graficar medias muestrales
LCS:
Línea central:
LCI:
Gráfica p: Graficar proporciones muestrales
LCS:
Línea central:
LCI: p 2 3
Å
pq
n
p
p 1 3
Å
pq
n
xx 2 A2R
xx
xx 1 A2R
x
D3R
R
D4R
Prueba de
rachas para
n Ͼ 20
z 5
G 2 mG
sG
5
G 2 a
2n1n2
n1 1 n2
1 1b
Å
(2n1n2)(2n1n2 2 n1 2 n2)
(n1 1 n2)2
(n1 1 n2 2 1)
avalor crítico para n . 30:
6 z
!n 2 1
b
rs 5 1 2
6Sd2
n(n2
2 1)
H 5
12
N(N 1 1)
a
R2
1
n1
1
R2
2
n2
1 . . . 1
R2
k
nk
b 2 3(N 1 1)
Prueba de suma de
rangos de Wilcoxon
(dos muestras
independientes)
z 5
R2mR
sR
5
R2
n1(n1 1n2 11)
2
Å
n1n2(n1 1n2 11)
12
z 5
T 2 n(n 1 1)>4
Å
n(n 1 1)(2n 1 1)
24
z 5
(x 1 0.5) 2 (n>2)
!n>2
Fórmulas y tablas
para Estadística, décima edición, de Mario Triola
D.R. © 2006 Pearson Educación de México S.A. de C.V.
Constantes de una gráfica de control
Tamaño
del subgrupo
n A2 D3 D4
2 1.880 0.000 3.267
3 1.023 0.000 2.574
4 0.729 0.000 2.282
5 0.577 0.000 2.114
6 0.483 0.000 2.004
7 0.419 0.076 1.924
Prueba de rangos con signo de
Wilcoxon (datos apareados y
n Ͼ 30)

4. ¿Está
el estadístico de
prueba a la derecha
o izquierda
del centro?
Valor P ϭ dos
veces el área a
la izquierda del
estadístico
de prueba
Valor P ϭ área
a la derecha del
estadístico de
prueba
Valor P ϭ dos
veces el área a
la derecha del
estadístico de
prueba
Valor P ϭ área
a la izquierda
del estadístico
de prueba
Valor P El valor P es dos
veces esta área
.
Estadístico de prueba Estadístico de prueba Estadístico de prueba Estadístico de prueba
El valor P es dos
veces esta área
Valor P
DerechaIzquierda
De cola izquierda De cola derecha
Dos colas
¿Qué
tipo de
prueba?
InicioCÁLCULO DE VALORES P
Sí
No
(La aseveración
original no contiene
igualdad y se convierte
en H1)
¿La
aseveración original
contiene la condición
de igualdad?
“Existe evidencia
suficiente que justifica
el rechazo de la
aseveración de que...
(aseveración original)”.
“No existe suficiente
evidencia que justifique
el rechazo de la
aseveración de que . . .
(aseveración original)”.
(La aseveración
original contiene
igualdad)
Sí
(Rechace
H0 )
“Los datos muestrales
sustentan la aseveración
de que . . . (aseveración
original)”
No
(No rechace H0 )
Sí
(Rechace
H0 )
No
(No rechace H0 )
“No existe evidencia
muestral suficiente para
sustentar la aseveración
original de que . . .
(aseveración original)”.
(Éste es
el único caso
en que se
sustenta la
aseveración
original)
(Éste es
el único caso
en que se
rechaza la
aseveración
original)
¿Se
rechaza
H0?
¿Se
rechaza
H0?
Redacción de
la conclusión final
Inicio PRUEBA DE HIPÓTESIS: REDACCIÓN
DE LA CONCLUSIÓN FINAL
Inferencias acerca de M: elección entre la distribución t y la distribución normal
Distribución t: Se desconoce s y la población se distribuye normalmente
o se desconoce s y n Ͼ 30
Distribución normal: Se conoce s y la población se distribuye normalmente
o se conoce s y n Ͼ 30
Método no paramétrico o “bootstrap”: La población no se distribuye normalmente y n Յ 30